Erdibideko

Geometrian, triangelu baten erdibidekoa zuzenki bat da, erpin bat eta aurkako aldearen erdiko puntua lotzen dituena. Trapezio batean, erdibidekoa bi alde ez-paraleloen erdiko puntuak lotzen dituen zuzenkia da.
Edozein triangeluk hiru erdibideko ditu: hiru erpinetatik aurkako aldera doazenak, eta barizentro, zentroide, grabitate-zentro edo masa-zentro —azken biak gehienbat Fisikan— deritzon puntuan ebakitzen dute elkar. triangelu isoszelearen eta triangelu aldekidearen kasuetan, erdibidekoak erdibitu egiten du luzera bereko alboko aldeak dituen angelua.
Nola kalkulatu erdibidekoaren luzera[aldatu | aldatu iturburu kodea]
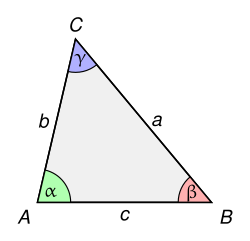
Triangelua[aldatu | aldatu iturburu kodea]
Artikulu nagusia: «Apolonioren teorema»
Erdibidekoen luzerak Apolonioren teoremaren bidez kalkula daitezke; honela:
non a, b eta c triangeluaren aldeak diren, eta ma, mb, eta mc haien erdibidekoak, hurrenez hurren.

Trapezioa[aldatu | aldatu iturburu kodea]
- Trapezio baten erdibidekoaren (x) luzera oinarrien (a eta c) luzeren baturaerdia da.
Ikus, gainera[aldatu | aldatu iturburu kodea]
Kanpo estekak[aldatu | aldatu iturburu kodea]
- (Ingelesez) The Medians (cut-the-knot)
- (Ingelesez) Medians of a triangle Animazio interaktiboarekin
- (Ingelesez) Constructing a median of a triangle with compass and straightedge Animazio interaktiboarekin
- (Ingelesez) Weisstein, Eric W.: "Triangle Median" MathWorld-en.




