Korronte alterno

Korronte alternoan[1] edo aldizkakoan (AC hizkiekin ere ezaguna, ingelesez Alternating Current), karga elektrikoen mugimenduaren noranzkoa aldizka aldatzen da, periodikoki, eta korrontearen balioa positiboa eta negatiboa da, aldizka. Korronte zuzenean, berriz, karga elektrikoak noranzko berean mugitzen dira, eta korronteak zeinu bera mantentzen du denboran zehar. Oro har, korronte hitza erabiltzen dugun arren, korronte aldizkatzaile eta korronte zuzen esateko, korrontearekin batera tentsioa ere adierazten da. Hortaz, tentsio aldizkatzaile eta tentsio zuzen esan dezakegu. Horregatik, sarri, seinale hitza erabili ohi da, korrontea eta tentsioa bereizi nahi ez direnean. 1. irudian hainbat seinale ageri dira: seinale aldizkatzaile sinusoidala (berdea), seinale zuzena (gorria), seinale aldakorra (grisa) eta seinale pultsuduna (urdina).
Etxeetara edota lantegietara iristen den argindarra korronte aldizkatzailea da. Korronte aldizkatzaileko zirkuituetan, uhin sinusoidala da erabiltzen den uhin-forma (ikus 2. irudia). Hala ere, beste erabilera batzuetan, bestelako uhin-formak erabiltzen dira, uhin triangeluarra edo uhin karratua, adibidez. Kable elektrikoetan garraiatu ohi diren audio- eta irrati-seinaleak ere korronte aldizkatzailearen adibideak dira. Aplikazio horietan, helburua da korronte aldizkatzaileko seinalearen baitan kodetutako (edo modulatutako) informazioa berreskuratzea.
Korronte aldizkatzaileko seinaleen matematika[aldatu | aldatu iturburu kodea]
v tentsio aldizkatzaile bat matematikoki adierazteko, denboraren mendekoa den eta honako ekuazio hau duen funtzio matematikoa erabiltzen da:
non:
- tentsio maximoa edo anplitudea () den (banakoa: volt),
- lastertasun angeluarra den (banakoa: radian segundoko)
- Lastertasun angeluarra seinalearen maiztasunarekin (, banakoa = hertz) lotuta dago, honako ekuazio honen bitartez: . Maiztasunak adierazten du zenbat aldiz errepikatzen den seinalea segundo batean, edo, gauza bera dena, seinalearen zenbat ziklo edo periodo sartzen diren segundo batean.
- denbora den (banakoa: segundo).
Tentsio aldizkatzaile baten piko-piko balioa mutur positiboaren eta mutur negatiboaren arteko diferentzia da. funtzioaren balio maximoa +1 denez, eta minimoa −1, tentsio aldizkatzailearen balioak eta artean aldatzen dira. Hortaz, tentsioaren piko-piko balioa, edo gisa adierazi ohi dena, hauxe da: .
Ahalmena eta balio eraginkorra[aldatu | aldatu iturburu kodea]
Korronte aldizkatzaileko zirkuitu batean erresistentzia bat baldin badago, honako erlazio matematiko hau betetzen da erresistentziak xurgatzen duen ahalmenaren eta bere muturren arteko tentsioaren artean:
Uneko ahalmena () erabili beharrean, praktikoagoa da batez besteko ahalmena erabiltzea (batezbestekoa kalkulatzeko, seinalearen ziklo-kopuru oso bat hartu behar da kontuan). Hala, bada, tentsio aldizkatzailea adierazteko, batezbesteko koadratikoa edo balio eraginkorra erabili ohi da :
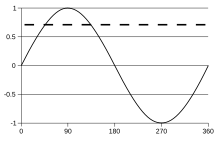
Tentsio sinusoidal baten kasuan:
faktoreari gandor faktore deritzo, eta ezberdina da uhin-forma desberdinetarako.
- Esate baterako, zero balioa duen ardatz horizontalaren inguruan hedatzen den uhin triangeluar baten kasuan:
- Eta zero balioa duen ardatz horizontalaren inguruan hedatzen den uhin karratu baten kasuan:
- uhin arbitrario baten kasuan, haren periodoa izanik:
Adibidea[aldatu | aldatu iturburu kodea]
Adigai horiek argitzeko, demagun 220 V-eko tentsio aldizkatzailea dugula (hori da tentsiorik erabiliena mundu zabaleko herrialde askotako argindar-sistemetan. Erabiltzen dugun balio hori, seinalearen balio eraginkorra da: 220 V. Horrek zera esan nahi du: denboran zehar korronte aldizkatzaileko seinaleak emandako batez besteko ahalmen 220 V-eko balio iraunkorra duen korronte zuzeneko tentsioak emango lukeenaren berdina dela. Korronte aldizkatzaileko seinalearen anplitudea (balio maximoa) kalkulatzeko, aurreko ekuazioa modu honetan berridatz dezakegu:
Hala, bada, eskuartean darabilgun 220 V-eko tentsio aldizkatzailearentzat, balio maximoa () hau da:, eta hori, gutxi-gorabehera, 311 V da. Eta seinale horren piko-piko balioa (), berriz, halako bi da: gutxi-gorabehera 622 V.
Korronte aldizkatzailearen ohiko maiztasunak[aldatu | aldatu iturburu kodea]
Argindar-sistemaren maiztasuna herrien arabera aldatzen da; gehienetan, 50 edo 60 hertz-eko seinaleak erabiltzen dira. Esate baterako, Europan, 50 Hz; Amerikako Estatu Batuetan, 60 Hz. Herrialde batzuetan, Japonian kasu, bi maiztasunetako sistemak dituzte: 50 Hz eta 60 Hz.
Erreferentziak[aldatu | aldatu iturburu kodea]
- ↑ «Zehazki - UPV/EHU» www.ehu.eus (Noiz kontsultatua: 2022-03-21).





























