Saltzaile ibiltariaren problema

Saltzaile ibiltariaren problemaren soluzioa: puntu gorri guztietatik behin bakarrik pasa eta hasierakoan amaitzen den ibilaldirik motzena.

Saltzaile ibiltariaren problema edo Bidaiariaren problema (ingelesez, Travelling Salesperson Problem, TSP), honakoa da: "hirien multzo bat izanik eta haien arteko distantziak ezagunak izanik, zein da hiri guztiak behin bakarrik bisitatu eta hasierako hirian amaitzen den ibilbiderik laburrena?". Ikerketa operatiboan eta konputazioaren zientzian garrantzia handia duen optimizazio konbinatorioko problema da. "Erosle Ibiltariaren Problema"-ren (Travelling Purchaser Problem, TPP) eta "Ibilgailuak Bideratzearen Problema"-ren (Vehicle Routing Problem, VRP) kasu partikularra da.

Problema 1930ean planteatu zen lehen aldiz eta optimizazio-problema konbinatorioen artean gehien aztertua izan denetako bat da. Haren ebazpenak duen konplexutasun konputazional altuagatik NP-Hard moduan sailkatua izan da. Hori dela eta, optimizazio-konbinatorioko problemen ebazpenerako sortzen diren metodo berrien eraginkortasuna neurtzeko erabiltzen da. Hain aztertua izan denez, ebazpen-metodo (zehatz eta heuristiko) asko ezagutzen dira. Horri esker, gaur egun tamaina handiko Bidaiariaren Problemak ebaztea posiblea da, milaka hirikoak barne. Problemaren bertsio hau NP-osoa da: "hirien multzo bat, haien arteko distantziak eta L luzera jakin bat emanik, hiri guztiak behin bakarrik bisitatu eta hasierako hirian amaitzen den ibilbiderik existitzen al da, gehienez L luzerakoa dena?".

Problemak aplikazio ugari ditu: plangintza-problemak, logistikako problemak, zirkuitu elektrikoen fabrikazioan agertzen direnak, etab. Gainera, problemaren planteamendua pixka bat aldatuta, jakintza-eremu askotan azpiproblema gisa agertu ohi da: DNAren sekuentziazioan, etab. Aplikazio horietan, “hiria” bezeroa izan daiteke, adibidez, edo soldadura-puntua, DNA zatia, etab. eta ibilbiderik laburrena aurkitzeko neurtu beharreko “distantzia” bidaia egiteko behar den denbora, ekoizpenaren kostua, DNA zatien arteko antzekotasuna, etab. Aplikazio askotan, problemaren ohiko murrizketez gain murrizketa gehigarriak egoten dira (mugatuta dauden baliabideak, kontuan hartu beharreko denbora-leihoak, etab.). Halakoetan, berez zaila den problemaren ebazpena are zailagoa gertatzen da.

Historia

Bidaiariaren problemaren jatorria ez dago argi. 1832an saltzaile ibiltarientzat idatzitako gida batean problema aipatzen da eta Alemanian eta Suitzan barrena diseinatutako ibilaldi batzuen adibideak ematen dira, baina ez da problema modu matematikoan aztertzen.

William Rowan Hamilton

Problemaren formulazio matematikoa W. R. Hamilton matematikari irlandarrak eta Thomas Kirkman matematikari britainiarrak eman zuten XIX. mendean. Hamiltonek "Icosian game" izeneko jokoa asmatu zuen. Puzzle moduko bat zen eta ziklo hamiltondar bat aurkitzea zuen helburu. Badirudi, matematikariek problemaren forma orokorra lehen aldiz 1930eko hamarkadan aztertu zutela Vienan eta Harvarden. Karl Menger-ek egindako lana aipagarria da, problema definitzeaz gain "indar gordinaren" algoritmo nabaria aztertu baitzuen, ingelesez "brute-force" izenez ezagutzen dena. Gainera, konturatu zen hiri batean hasi eta urrats bakoitzean gertuen dagoen hirira joateak ez duela ziurtatzen hiri guztietatik pasatzen den ibilbide motzena aurkituko denik. Horrela adierazi zuen:

“Mezulariaren problema” (praktikan mezulariei edo bidaiariei sortuko baitzaie problema ebazteko beharra) horrela defini daiteke: puntuen multzo finitu bat izanik eta haietako edozein biren arteko distantzia ezaguna izanik, puntuak konektatuko dituen biderik laburrena aurkitzea. Jakina, saiakera kopuru finitu batean problema ebaztea lortzen da. Hirien permutazio guztiak aztertzeak eskatzen duen saiakera kopurua baino gutxiagotan biderik laburrena aurkitzeko baliagarriak diren erregelak ez dira ezagutzen. Honako erregela jarrai daiteke: hasierako puntutik gertuen dagoen puntura joatea, hortik hurbilen dagoen beste puntura, etab. Hala ere, erregela horrekin, oro har, ez du biderik laburrena aurkitzen.

1930eko hamarkadan Merrill M. Floode-ek lehen planteamendu matematikoa egin zuen, eskola-autobusen bideratzearen problema aztertzen ari zenean. Gerora, Princetongo Unibertsitateko Hassler Whitney-k problemarako interesa piztu zuen. Berak problema "48 states problem" moduan izendatu zuen. Julia Robinson-ek 1949an RAND korporaziorako idatzi zuen txosten batean argitaratu zen lehen aldiz problemaren aipamena "Travelling Salesman Problem" izenarekin, "On the Hamiltonian game (a traveling salesman problem)".

1950eko eta 1960ko hamarkadetan Santa Monicako RAND korporazioa problemaren ebazpenean aurrerapausoak ematen zituzten zientzialariei sariak eskaintzen hasi zenean, problema gero eta ezagunagoa bihurtu zen Europan eta Estatu Batuetan. Korporazioko George Dantzig-ek, Delbert Ray Fulkerson-ek eta Selmer M. Johnson-ek ekarpen nabarmenak egin zituzten. Problema lineal oso gisa planteatu zuten eta ebazpenerako ebaki-planoen metodoa garatu zuten. Metodo berri horren bidez 49 hiriko instantzia bat ebaztea lortu zuten, hiriak konektatzen zituen ibilbidea osatu zuten eta frogatu zuten ibilbide hori baino motzagorik ez dela existitzen. Haien argitalpena problemaren ikerketarako hazia izan zela esaten da, ebazpen-metodoetan emankorra izan den ikerketa-arlo baten hasiera. Pentsatu zuten ia optimoa den soluzio bat izanik posiblea izango zela soluzio optimoa aurkitzea edo optimaltasuna frogatzea, desberdintza (inekuazio, murrizketa, ebaki-plano) kopuru txiki bat erantsiz. Ideia horretan oinarritu ziren 49 hiriko problema ebazteko, eta konturatu ziren 26 ebaki-plano besterik ez zirela behar. Artikulu horretan Bidaiariaren Problemaren ebazpenerako algoritmorik eman ez zuten arren, bertan argitaratu zituzten ideiak ezinbestekoak izan ziren gerora ebazpen-metodo zehatzak garatzeko. Beste 15 urte behar izan ziren ebaki-plano egokiak aurkitzeko metodo algoritmikoa garatzeko. Ebaki-planoen metodoaz gain, Dantzigek, Fulkersonek eta Johnsonek adarkatze- eta bornatze-algoritmoak erabili zituzten, historian lehen aldiz, agian.

1972. urtean, Richard M. Karp-ek frogatu zuen grafo batean ziklo Hamiltondarra aurkitzearen problema NP-osoa dela, eta horrek esan nahi du Saltzaile Ibiltariaren Problema NP-Hard dela. Horrela, Bidaiariaren Problemarako ibilbide motzena aurkitzeak itxuraz zuen zailtasun konputazionalari azalpen matematiko bat ematea lortu zen.

1970eko hamarkadaren amaieran eta 1980ko hasieran aurrerapen handiak lortu ziren, Grötschel-ek, Padberg-ek, Rinaldi-k eta beste ikerlari batzuek ebaki-planoen metodoa eta adarkatze- eta bornatze-algoritmoa erabiliz 2.392 hiriko instantziak ebazteaz lortu zutenean.

1990eko hamarkadan, Applegate-k, Bixby-k, Chvátal-ek eta Cook-ek "Concorde" programa garatu zuten eta hura erabiliz problema asko ebaztea lortu zen. 1991ean Gerhard Reineltek "TSPLIB, A Traveling Salesman Problem Library" izeneko liburutegia argitaratu zuen. Zailtasun-maila desberdineko problemen bilduma bat da eta ikerketa-talde askok probarako erabiltzen dituzte, haien metodoekin lortutako emaitzak beste ikerlariek lortutakoekin alderatzeko.

2006an, Cook-ek eta beste ikerlari batzuek mikrotxipen diseinuaren problematik sortutako 85.900 hiriko instantzia ebaztea lortu zuten, ebaztea lortu den TSPLIB liburutegiko instantziarik luzeena. Milioika hiriko problemetarako, hirien arteko ibilbide bat aurkitzen duten metodoak badaude, baina ez da bermatzen hirien arteko bide motzena izango denik.

Sarrera

Problema konbinatorioa

Saltzaile ibiltariaren problema optimizazio konbinatorioko problema bat da. $n$ hiriren arteko distantziak izanik, hiri guztietatik pasa eta hasierakoan amaitzen den biderik laburrena aurkitu behar da. Hiri guztietatik pasatzen diren ibilbide asko daude. Zenbat diren kontatzeko, konbinatoria erabil daiteke: $n$ elementuren ordenazio posible guztiak $n$-ren permutazioak dira. Optimizazio problema bat da, guztien artetik optimoa aurkitu nahi delako, kasu honetan, ibilbiderik motzena. $n$-ren balioa handitzen bada, aukera posibleen kopurua asko hazten da.

Adibidez, 3 hiriko saltzaile ibiltariaren probleman 6 ibilbide daude: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1). Hiru elementuren permutazioak dira, hau da, elementuen ordenazio posible guztiak. Bidaiariaren probleman, (1, 2, 3) permutazioarekin zera adierazten da: bidea 1 hirian hasten da, ondoren 2 hirira doa, gero 3 hirira eta 1 hirian amaitzen da. Permutazio kopurua n-ren faktoriala da, normalean n! ikurraz adierazten dena. Hirien kopurua handitzean, ordenazio kopurua asko hazten da. 3!=6 da, 10!=3628800, 100!=9.33 × 10¹⁵⁷.

Kopuru hori murriztu daiteke, bidea hasi eta bukatu hiri berean egiten denez eta abiapuntua zein den adierazten ez denez, (1, 2, 3), (2, 3, 1) eta (3, 1, 2) permutazioek bide bera adierazten dute: 1tik 2ra, 2tik 3ra eta 3tik 1era. Gauza bera gertatzen da beste hiru permutazioekin, hirien arteko ibilbide bera adierazten dute: (1, 3, 2), (3, 2, 1), (2, 1, 3). Hortaz, berez hiru hiriren artean 2 ibilbide desberdin besterik ez daudela esan daiteke. Ibilbide kopuruaren kontaketa murrizten da, aukera posible guztiak zati $n$, hau da, $n$!/$n$= ($n$-1)! ibilbide dira. $n$=3ren kasuan, 2!=2 ibilbide.

Gainera, saltzaile ibiltariaren probleman bidaiaria zein norabidetan mugitzen den ez du axola, hau da, 1tik 2ra, 2tik 3ra eta 3tik 1era joatea edo 3tik 2ra, 2tik 1era eta 1etik 3ra joatea ibilbide bera egitea dela interpretatzen da. Horrek aztertu beharreko ibilbideen kopurua erdira murrizten du. Beraz, ($n$-1)!/2 ibilbide posible hartu behar dira kontuan.

• $n$=10 hiriko probleman, (10-1)!/2=181.440 ibilbide desberdin daude
• $n$=30 hiriko probleman, (30-1)!/2=4.42 × 10³⁰ ibilbide baino gehiago daude. Segundoko milioi bat ibilbide kalkulatzen dituen ordenagailuak 10¹⁷ urte beharko lituzke ebazteko. Bestela esanda, unibertsoaren sorreraren hasieran kalkulatu izan balitz (duela 13.400 milioi urte inguru) kalkulua oraindik amaitu gabe egongo litzateke.

Ikus daitekeenez, problemari gehitzen zaion hiri bakoitzeko, ibilbide kopurua $n$ faktoreaz biderkatzen da, eta bide motzenaren problemaren ebazpena modu faktorialean hazten da. Horregatik, esaten da problema NP-osoa dela.

Grafo-adierazpena

4 hiriko Saltzaile Ibiltariaren problema baten grafo-adierazpena, grafo haztatu ez-zuzendu eta simetriko baten bidez

Saltzaile Ibiltariaren Problema grafo haztatu ez-zuzendu gisa adieraz daiteke, non grafoko erpinak hiriak diren, ertzak hirien arteko bideak diren eta ertzen pisuak (edo kostuak) bideen distantziak diren. Grafoko ertzek noranzkorik ez badute, hau da, bi noranzkoetan zeharka badaitezke, ez-zuzendua dela esaten da. Minimizazio-problema bat da, erpin guztiak behin bakarrik zeharkatu eta hasierako erpinean amaitzen den distantzia minimoko ibilaldia bilatzen delako.

Problemaren ohiko planteamenduan, eredua grafo oso bat da, hau da, erpin-pare guztiak daude konektatuta ertzen bidez. Problema partikular batean bi hiriren artean biderik ez badago eta grafo oso baten bidez adierazi nahi bada, bi hiri horien artean pisu handia esleitua duen ertz bat jar daiteke, bi hiri horiek haien artean oso urruti daudela adierazi nahiko balitz bezala. Horrela, grafo osoetarako ebazpen-metodoak aplikatu ahal izango dira. Pisua nahiko handia bada, metodoak aurkituko duen ibilbide motzena ez da bi hiri horien artetik pasako, berez existitzen ez den bidetik ez da pasako, eta ez da arazorik sortuko.

Saltzaile ibiltariaren problema matrize baten bidez ere adieraz daiteke, grafoei lotutakoauzokidetasun-matrizeen bidez.

Simetria

Hirien arteko distantzia bi noranzkoetan berdina bada, Saltzaile ibiltariaren problema simetrikoa dela esaten da eta grafo ez-zuzendu baten bidez adierazten da. Horrek aztertu beharreko ibilbideen kopurua erdira murrizten du, ibilaldia noranzko batean egitea edo kontrakoan egitea gauza bera dela ulertzen delako. Problema auzokidetasun-matrize baten bidez adieraziz gero, hura adierazten duen matrizea simetrikoa izango da.

Bidaiariaren problema asimetrikoa izan daiteke, hau da, gerta daiteke bi hiriren artean bidea egotea noranzko batean baina ez egotea kontrako noranzkoan, edo distantziak desberdinak izatea noranzko bakoitzean. Halako problemak grafo zuzenduen bidez adierazten dira eta ertzak gezien bidez ematen dira. Zirkulazio-istripuak, noranzko bakarreko kaleak edo abiatze- eta lehorreratze-kostu desberdinak dituzten aire-tarifek, adibidez, problemaren simetria hausten dute.

Erlazionatutako problemak

Saltzaile ibiltariaren problemarekin erlazioa duten hainbat problema daude. Hona hemen batzuk:

• Grafoen teorian, bidaiariaren problema ebaztea grafo oso eta haztatu batean (erpinak hiriak dira, ertzak bideak dira eta kostuak distantziak dira), kostu minimoko ziklo hamiltondarra aurkitzea da. Ibilbidea ixteko hasierako hirira itzuli behar izateak ez du aldatzen problemaren konplexutasun konputazionala eta ondorioz, grafoan bide hamiltondar bat aurkitzearen problemak konplexutasun bera du.

• "Bidaiariaren Problema Botila-lepoduna" (ingelesez, Bottleneck, TSP): Grafo oso eta haztatu batean kostu handieneko ertzaren pisua minimizatzen duen ziklo hamiltondarra aurkitu behar da. Problema horrek garrantzi handiko aplikazioak ditu, garraioaren arloan eta logistikan, autobusek kale estuak edo trafiko handienekoak ekiditeko, adibidez. Beste aplikazio klasiko bat zirkuitu inprimatuen fabrikazioa da (ingelesez, printed circuit board, PCB). Osagaiak bertan kokatzeko plaka zulatu behar da eta zulagailuaren ibilbidea planifikatu behar da. Halako zulagailu edo robotetan bidaiariaren problema aplikatzen denean, “hiriak” egin beharreko zuloak dira (tamaina desberdinekoak izan daitezke), eta “kostuak” zulo bat egitetik bestera pasatzeak eskatzen duen berrantolaketa, denbora barne. Azken batean, makina batean hainbat lanen sekuentziazioa optimizatzearen problema da

• "Saltzaile ibiltariaren problema orokortua" edo "Politikari Bidaiariaren Problema". Problemaren planteamendu orokortuan, “hiri” bat edo gehiago dituzten “estatuak” daude eta bidaiariak bere ibilbidean “estatu” bakoitzeko hiri bat bisitatu behar du. Planteamendu honek ere aplikazioak ditu erdieroaleen fabrikazioan, zulagailuaren ibilbidearen planifikazioan (ikus USPTO patentea, 7054798 zk.). Harrigarria badirudi ere, Behzad-ek eta Modarres-ek frogatu zuten problemaren planteamendu orokortua hiri kopuru bera duen bidaiariaren problema estandar bihur daitekeela, hirien arteko distantzien matrizea aldatuz.

• "Ordenazio Sekuentzialaren Problema" bidaiariaren problemaren antzekoa da, baina hirien artean dauden lehentasun-erlazioak (hiri bat bisitatu aurretik zein beste hiri bisitatu behar diren) ere kontuan hartu behar dira.
• Google-i sortzen zaion problema bat hau da: nola bideratu datuak datu-prozesaketarako nodoen artean. Kontuan izan behar da, datuak nodoen artean transferitzeko behar den denbora desberdina izan daitekeela, baita nodoen kalkulu-ahalmena eta biltegiratze-ahalmena ere. Horren arabera, ibilbideak aldatu egiten dira eta datuak nodoetara bideratzearen problema zailagoa gertatzen da.

• "Erosle Ibiltariaren Problema" (ingelesez, Travelling Purchaser Problem, TPP). Erosle batek produktu batzuk erosi behar ditu. Produktu horiek hainbat hiritan eros daitezke, baina hiri guztiek ez dituzte produktu berak eskaintzen. Gainera, produktu berak hiri desberdinetan prezio desberdinak izan ditzake. Hirien azpimultzo batetik pasatzen den ibilbidea aurkitzea da helburua, ibilbideko hirietan erosi beharreko produktu guztiak erostea posiblea dela bermatuz eta kostu totala (bidaiarena + erosketarena) minimizatuz.

Problemaren formulazioa

Saltzaile ibiltariaren problema programazio lineal osoko problema gisa formula daiteke. Hiriak 1-etik $n$-rako zenbakien bidez izendatzen dira eta $i$ hiritik $j$ hirira dagoen distantzia (joateak eragiten duen kostua) $c_{ij}$ notazioaz adierazten da, $i,j\in \{1,\cdots ,n\}$ izanik.

Erabaki-aldagaiak bitarrak dira, hau da, 0 (zero) edo 1 (bat) balioetara mugatzen dira, eta horrela definitzen dira:

$x_{ij}={\begin{cases}1&{\text{baldin bidaiaria}}\ i\ {\text{hiritik}}\ j\ {\text{hirira badoa}}\\0&bestela\end{cases}}$

Horrela, $x_{ij}=1$ bada, ibilbidea $i$ hiritik $j$ hirira doala esan nahi du. Problemaren helburua kostu txikieneko ibilbidea aurkitzea denez, helburu-funtzioa horrela definitzen da:

$min\ z=\sum _{i=1}^{n}\sum _{j\neq i,j=1}^{n}c_{ij}x_{ij}$

Bidaiariak egingo duen ibilbidea hiri guztietatik pasa behar da, eta bakoitzetik behin bakarrik. Hori hala izan dadin, hainbat murrizketa gehitu behar dira formulazioan. Alde batetik, bidaiaria $j$ hiri bakoitzera $i$ hiri bakar batetik joango dela ziurtatzeko, $j$ bakoitzerako $x_{ij}$ aldagaien batura 1 dela adierazten duen murrizketa idazten da. Bidaiariak $n$ hiri bisitatu behar dituenez, $j$-ren balio bakoitzerako ($j=1,\dots ,n$) horrelako murrizketa bat dago:

$\sum _{i=1,i\neq j}^{n}x_{ij}=1$

Bestalde, ibilbidea $i$ hiri bakoitzetik $j$ hiri bakar batera joango dela ziurtatzeko, $i$ bakoitzerako $x_{ij}$ aldagaien batura 1 dela adierazten duen murrizketa idazten da. Bidaiaria $n$ hirietatik irtengo denez, $i$-ren balio bakoitzerako ($i=1,\dots ,n$) horrelako murrizketa bat dago:

$\sum _{j=1,j\neq i}^{n}x_{ij}=1$

Murrizketa horiek ziurtatzen dute bidaiaria hiri batean dagoenean ez dela beste bi hiritara joango, edo hiri batera ez dela beste bi hirietatik iritsiko. Funtzio eta ekuazio horiek guztiak linealak direnez eta erabaki aldagaiak osoak (bitarrak) direnez, programazio lineal osoko formulazioa lortzen da.

Hala ere, murrizketa horiek ez dira nahikoak saltzaile ibiltariaren problema adierazteko, ez delako bermatzen hiri guztiak ibilaldi bakar batean bisitatuko direnik. Adibide gisa, hurrengo taulan $n=4$ hirirako soluzio bat aurkezten da: $x_{12}=1$, $x_{21}=1$, $x_{34}=1$, $x_{43}=1$, eta gainerako aldagai guztiak zero. Taulan ikusten den bezala, 1eko bakarra dago zutabeetan (hiri bakoitzera beste bakar batetik iristen da) eta 1eko bakarra errenkadetan (hirietatik beste hiri bakar batera doa). Planteatu diren murrizketa guztiak betetzen ditu, baina ez du ibilaldi bakar bat osatzen, bi azpi-ziklo baizik: 1etik 2ra eta 2tik 1era (azpi-ziklo bat), 3tik 4ra eta 4tik 3ra (beste azpi-ziklo bat). Hortaz, soluzio horrek ez du bidaiariaren problema ebazten.

$n=4\ {\text{hiri}},\ x_{ij}\ {\text{soluzio bat}}$

	$1$	$2$	$3$	$4$
$1$	$0$	$1$	$0$	$0$
$2$	$1$	$0$	$0$	$0$
$3$	$0$	$0$	$0$	$1$
$4$	$0$	$0$	$1$	$0$

Problemaren soluzio ez diren horrelako kasuak baztertzeko, beste murrizketa bat gehitu behar da formulazio matematikoan. Planteamendu desberdinak egin izan diren arren, honako biak nabarmentzen dira: "Miller–Tucker–Zemlin (MTZ)" formulazioa eta "Dantzig–Fulkerson–Johnson (DFJ)" formulazioa. Bigarrena sendoagoa bada ere, lehenengoa hainbat egoeratan erabilgarria da.

Miller–Tucker–Zemlin formulazioa (MTZ)

MTZ formulazioan $x_{ij}$ aldagaiak erabiltzeaz gain, honako $u_{i}$ aldagaiak definitzen dira hiriak zein ordenatan bisitatuko diren kontrolatzeko:

$u_{i}=i\ {\text{hirira zenbat urratsetan iritsiko den}},i=2,\cdots ,n$

Ibilbidea 1 hirian hasten dela suposa daiteke, orokortasunik galdu gabe. Horregatik, $u_{i}$ aldagaiaren azpi-indizeak ez du 1 balioa hartzen. Aldagaietan urrats kopurua adierazten denez, $u_{i}\in \{1,\dots ,n-1\}$ balioak har ditzake. Izan ere, $n$ hiriko ibilbidea osatzeko $n-1$ urrats eman behar dira eta horri jakina den azken urrats bat gehitu: hasierako hirira itzultzea, 1 hirira, alegia.

$u_{j}>u_{i}$ desberdintzak zera adierazten du: $j$ hirira iristeko eman behar den urrats kopurua $i$ hirira iristeko eman behar dena baino handiagoa da. Horrek hirien artean ordena bat finkatzen du. $x_{ij}$ aldagaiak $u_{i}$ eta $u_{j}$ aldagaiekin erlazionatu behar dira, ibilaldi bakar batean hiri guztiak zeharkatzen direla ziurtatzeko, hau da, azpi-zikloak ekiditeko. Hori honako murrizketarekin lortzen da:

$u_{i}-u_{j}+(n-1)x_{ij}\leq n-2,$

$i,j=2,\dots ,n,\ i\neq j$ izanik. Egiazta daiteke $x_{ij}=1$ denean $u_{j}\geq u_{i}+1$ betetzen dela. Koherentea da esatea ibilaldia $i$ hiritik $j$ hirira doala eta $j$ hirira iristeko behar den urrats kopurua $i$ hirira iristeko behar dena baino handiagoa dela. Bestalde, $x_{ij}=0$ denean $u_{j}+n-1\geq u_{i}+1$ erlazioa lortzen da, hau da, $u_{i}$ eta $u_{j}$ aldagaien artean ez da murrizketarik ezartzen, $u_{j}+n-1\geq u_{i}+1$ beti betetzen delako (kasurik okerrenean $u_{j}=1$ eta $u_{i}=n-1$ izanik, erlazioa $n=n$ izango da). Gainera, egiazta daiteke ibilbidea azpi-zikloz osatzen bada, murrizketa horiek kontraesanera eramaten dutela, $k$ luzerako azpi-zikloetarako $k(n-1)\leq k(n-2)$ kontraesera.

Miller-Tucker-Zemlin formulazioaren arabera, eredu lineala bere osotasunean horrela geratzen da:

$min\ z=\sum _{i=1}^{n}\sum _{j\neq i,j=1}^{n}c_{ij}x_{ij}$

${\text{hauen mende:}}\quad \quad \quad \quad \quad \quad \quad$

${\begin{cases}\displaystyle \sum _{i=1,i\neq j}^{n}x_{ij}=1&\ j=1,\dots ,n;\\\displaystyle \sum _{j=1,j\neq i}^{n}x_{ij}=1&\ i=1,\dots ,n;\\u_{i}-u_{j}+(n-1)x_{ij}\leq n-2&\ i,j=2,\dots ,n,\ i\neq j;\\u_{i}\in \{1,\dots ,n-1\}&i=2,\dots ,n;\\x_{ij}\in \{0,1\}&i,j=1,\dots ,n.\end{cases}}$

Aurreko adibidearekin segituz, $n=4$ hiri daude, $x_{12}=1$, $x_{21}=1$, $x_{34}=1$, $x_{43}=1$ dira eta gainerakoak zero. Egiazta daiteke MTZ formulazioan erantsitako aldagaien eta murrizketaren eragina.

$x_{34}=1\quad \rightarrow \quad u_{3}-u_{4}+(n-1)x_{34}\leq n-2\quad \rightarrow \quad u_{3}-u_{4}+n-1\leq n-2\quad \rightarrow \quad u_{4}\geq u_{3}+1$

$x_{34}$, $u_{3}$ eta $u_{4}$ aldagaien artean erlazio koherentea ezartzen da.

$x_{23}=0\quad \rightarrow \quad u_{2}-u_{3}+(n-1)x_{23}\leq n-2\quad \rightarrow \quad u_{2}\leq u_{3}+(n-2)$

$n=4$ izanik, kasurik okerrenean $u_{3}=1$ bada $u_{2}\leq 3$ geratzen da. Beraz, $u_{2}$ eta $u_{3}$ aldagaien balio guztietarako murrizketa betetzen da. Ibilbidea ez doanez 2 hiritik 3ra, ez da haien artean ordenarik ezartzen.

Bestalde, $x_{34}=1$ eta $x_{43}=1$ azpi-ziklorako kontraesana sortzen da.

$x_{34}=1\quad \rightarrow \quad u_{3}-u_{4}+(n-1)x_{34}\leq n-2,\quad \quad {\text{ eta }}\quad \quad x_{43}=1\quad \rightarrow \quad u_{4}-u_{3}+(n-1)x_{43}\leq n-2$

Bi ekuazioak berdintzaren bi ataletan batuz $2(n-1)\leq 2(n-2)$ kontraesana den erlazioa lortzen da (sinplifikatuz, $n\leq n-1$). Beraz, azpi-zikloak ez dira sortuko.

Dantzig–Fulkerson–Johnson formulazioa (DFJ)

DFJ formulazioan "azpi-ibilbideak ezabatzeko murrizketak" (ingelesez, subtour elimination constraint) gehitzen dira. $n$ hiriko bidaiariaren problemarako, $Q\subsetneq \{1,\dots ,n\}$ azpimultzo propioak definitzen dira. $Q$ azpimultzoen kardinalak (elementu kopuruak) gutxienez bikoa izan behar du, $|Q|\geq 2$. Sor daitezkeen azpi-ziklo guztiak ezabatzeko, $n$ elementurekin osa daitezkeen halako $Q$ azpimultzo posible guztietarako definitzen diren murrizketak honakoak dira:

$\sum _{i\in Q}\sum _{j\neq i,j\in Q}x_{ij}\leq |Q|-1$

Inekuazioaren ezkerraldeko bi batukari horien bidez $Q$ azpi-zikloan dagoen ertz kopurua kontatzen da eta kopuru hori azpi-zikloan dagoen hiri kopurua baino txikiagoa dela ziurtatzen du murrizketak. Horrela lortzen da azpi-zikloak baztertzea eta hiri guztietatik behin igarotzen den ziklo bakar batez osatutako ibilaldia aurkitzea.

Dantzig–Fulkerson–Johnson formulazioa honakoa da:

$min\ z=\sum _{i=1}^{n}\sum _{j\neq i,j=1}^{n}c_{ij}x_{ij}$

${\text{hauen mende:}}\quad \quad \quad \quad \quad \quad \quad$

${\begin{cases}\displaystyle \sum _{i=1,i\neq j}^{n}x_{ij}=1&\ j=1,\dots ,n;\\\displaystyle \sum _{j=1,j\neq i}^{n}x_{ij}=1&\ i=1,\dots ,n;\\\displaystyle \sum _{i\in Q}\sum _{j\neq i,j\in Q}x_{ij}\leq |Q|-1&\forall Q\subsetneq \{1,\dots ,n\},\ |Q|\geq 2\\x_{ij}\in \{0,1\}&i,j=1,\dots ,n.\end{cases}}$

$n$ handitzearekin batera, ereduari gehitzen zaion murrizketa kopurua izugarri hazten da. Formulazioa proposatu zuten ikerlariek ikusi zuten guztiak gehitzea ez dela beharrezkoa, formulazioa sinplifikatuz.

Aurreko adibidearekin segituz, $n=4$ izanik, $Q\subsetneq \{1,2,3,4\}$, $|Q|\geq 2$ azpimultzo propioak definitu behar dira. Hainbat aukera daude, bi hirik osatutako azpimultzoak ($Q=\{1,2\}$, adibidez) edo hiru hirik osatutakoak ($Q=\{2,3,4\}$, adibidez). Adibidean bi azpi-zikloz osatutako $x_{12}=1$, $x_{21}=1$, $x_{34}=1$, $x_{43}=1$ soluziorako, har dezagun $Q=\{3,4\}$ azpimultzo propioa, non $|Q|=2$ den. 3 eta 4 hirien arteko azpi-zikloan, egiazta daiteke DFJ formulazioan gehitutako murrizketak sortzen duen eragina:

$\sum _{i\in Q}\sum _{j\neq i,j\in Q}x_{ij}\leq |Q|-1\quad \quad \rightarrow \quad \quad x_{34}+x_{43}\leq 2-1\quad \quad \rightarrow \quad \quad 2\leq 1$

Azpi-zikloan 2 ertz daude (3tik 4ra eta 4tik 3ra) eta 2 erpin (3a eta 4a). Dagoen ertz kopurua erpin kopurua baino txikiagoa izatera behartzeak kontraesanera eramaten du, azpi-zikloaren sorrera ekidinez. Azpi-ziklo posible guztiak kontraesanera eramanez, problemaren ebazpenean hiri guztietatik pasatzen den ziklo bakarreko ibilaldia lortuko da.

Problemaren ebazpena

Bidaiariaren problemaren ebazpenak duen konplexutasunagatik, problema NP-gogor moduan sailkatua izan da. Horrelako problemen soluzio optimoa aurkitzeko ahaleginean, estrategia desberdinak erabili izan dira:

• Algoritmo zehatzak diseinatzea soluzio optimoa aurkitzeko. Tamaina txikiko problemekin gai dira soluzioa aurkitzeko zentzuzko denbora erabiliz.
• Algoritmo heuristikoak diseinatzea, soluzio optimoaren hurbilketa aurkitzeko gai direnak zentzuzko denbora erabiliz. Tamaina handiko problemen ebazpenean eraginkorrak izan daitezke, baina ez dute bermatzen soluzio optimoa (optimo globala) aurkituko dutenik; optimo lokalak aurkitzen dituzte.
• Problemaren kasu partikularrak (azpiproblemak) bilatzea, non horiek ebazteko algoritmo zehatzak edo metodo heuristiko hobeak aplikatzea posiblea den.

Algoritmo zehatzak

n=7 hiriko instantzia baten ebazpena indar gordinaren algoritmoa erabiliz. Permutazio kopurua n!=7!= 5040 da. (7-1)!/2 = 360 ibilbide desberdin aztertzen dira.

Lehen begiratuan, problema ebazteko metodo zuzenena ibilbideen konbinaketa guztiak aztertzea dela pentsa daiteke, hau da, hirien permutazio (ordenazio) desberdin guztiak aztertzea eta haien artean kosturik txikienekoarekin (ibilbide motzenarekin) geratzea. Estrategia horri "indar gordinaren" algoritmoa esaten zaio (ingelesez "brute-force"), aukera guztiak aztertzen direlako. Hortaz, soluzio optimoa aurkitzea bermatzen da, baina konplexutasun-konputazionalaren ikuspegitik bideraezina da, $n$ hiriko problema ebazteko algoritmoak $O(n!)$ ordeneko konplexutasuna duelako. Esaterako, 20 hiriko problema bat indar gordinaz ebaztea praktikan ezinezkoa litzateke, zentzuzko denboran soluzio optimoa aurkitu nahi bada, behintzat.

Hori kontuan izanik, algoritmo konplexuagoak diseinatu izan dira. Held-Karp algoritmoa, adibidez, programazio dinamikoan oinarritzen da eta problema $O(n^{2}2^{n})$ denboran ebaztea lortzen da. Antzeko konplexutasun-ordeneko algoritmo zehatzak diseinatu izan dira, baina denbora-muga hori gainditzea zaila gertatzen da. Izan ere, oraindik ez da frogatu $O(1,999^{n})$ konplexutasun-ordena baino txikiagoa duen algoritmo zehatzik existitzen den.

n=7 hiriko instantzia baten ebazpena adarkatze- eta bornatze-algoritmo bat erabiliz. Aztertzen den permutazio kopurua askoz txikiagoa da indar gordinaren algoritmoan baino.

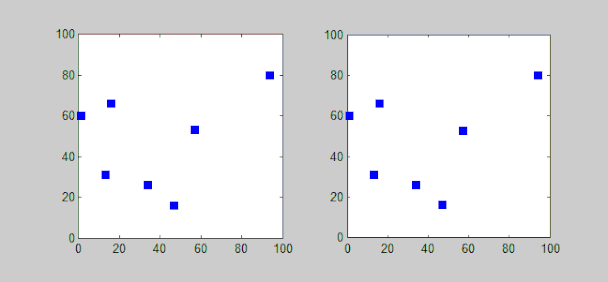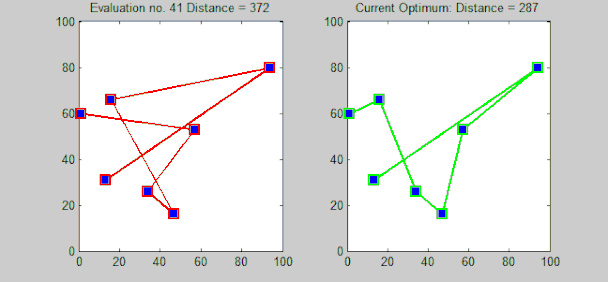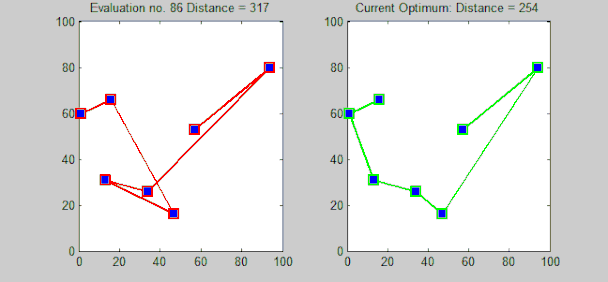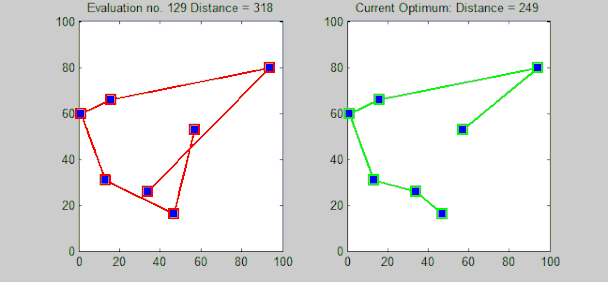
Hona hemen bidaiariaren problema ebazteko garatu izan diren beste algoritmo zehatz batzuk:

• Adarkatze- eta bornatze-algoritmoaren hainbat bertsio daude $n=40$ eta $n=60$ hiri arteko bidaiariaren problema ebaztean ondo moldatzen direnak.

• Hobekuntza progresiboko algoritmoek programazio linealaren antzeko teknikak erabiltzen dituzte. $n=200$ hirira arteko problemen ebazpenean ondo dabiltza.
• Badira adarkatze- eta bornatze-algoritmoaren bertsio batzuk eta baita problemarako mozte espezifikoak sortzeko diseinatutako algoritmoak (adarkatze- eta ebakitze-algoritmoak) tamaina handiko instantziak ebaztean ondo funtzionatzen dutenak. Algoritmo horiek erabiliz $n=85.900$ hiriko saltzaile ibiltariaren problemaren instantzia bat ebaztea lortu da.

Algoritmo zehatz horiek bizitza errealeko bidaiariaren problemaren instantziak ebazteko erabili izan dira historian zehar. Adibidez, 2001ean 15.112 hiri alemaniarrez osaturiko problemaren soluzio zehatza aurkitzea lortu zen ebaki-planoen metodoa erabiliz. 2004ean Suediako 24.978 hiriko problema ebatzi zen, 72.500 kilometro inguruko ibilbide bat aurkitu zen eta frogatu zen ibilbide hori baino motzagorik ez dela existitzen.

Algoritmo heuristikoak

Algoritmo heuristikoak soluzio optimoaren hurbilketak aurkitzen dituzten algoritmoak dira. Ez dute bermatzen soluzio optimoa (optimo globala) aurkituko denik, eta ondorioz, optimo lokalak ematen dituzte emaitza moduan. Normalean algoritmo horiek tamaina handiko problemak ebazteko erabiltzen dira, optimora iristeko beharko litzatekeen denboragatik metodo zehatzak erabiltzea ezinezkoa gertatzen den kasuetan. Halakoetan, algoritmo heuristikoak erabiltzea eraginkorra izan daiteke.

Azken urteotan soluzio optimora asko hurbiltzen diren algoritmo heuristiko anitz diseinatu dira saltzaile ibiltariaren problema ebazteko. Helburua tamaina handiko instantziekin ahalik eta soluzio onena lortzea da, zentzuzko denbora erabiliz. Ikusi da algoritmo heuristiko modernoak soluzio optimo globaletik $\%3$ inguru besterik ez direla aldentzen. Algoritmo heuristikoen artean, mota desberdinekoak daude.

Algoritmo eraikitzaileak (irenskorrak)

Auzokide hurbilenaren algoritmoak hasierako hiri desberdinetatik hasita ibilbide desberdinak eraikitzen ditu. Adibidez, A-B-C-D eta bueltan Ara (97ko distantzia) edo C-D-B-A eta bueltan Cra (108koa)

Algoritmo eraikitzaileek (ingelesez, "constructive") soluzioa urratsez urrats eraikitzen dute, normalean urrats bakoitzean aukerarik onena hautatuz eta problemaren ezaugarriak kontuan hartuz, hau da, intuizioa erabiliz. Algoritmo hauei algoritmo irenskor (ingelesez, "greedy algorithm") ere deitu ohi zaie, soluzioa eraikitzean urrats guztietan aukerarik onena hautatzen dutelako. Eraginkorrak izaten dira soluzio onak aurkitzeko, baina problema espezifiko bakoitzerako diseinatzen direnez, beste problemetara egokitzeko zailak izaten dira. Saltzaile ibiltariaren problemarako algoritmo eraikitzaile bat "auzokide hurbilenaren algoritmoa" da. Algoritmo horretan ibilbidea hasteko hiri bat aukeratzen da, eta hirien arteko distantziak aztertuz, oraindik bisitatua izan ez den eta gertuen dagoen hirira joatea erabakitzen da, urratsez urrats.

Auzokide hurbilenaren algoritmoaren aplikazio dinamikoa 7 hiriko instantzia batean. Hasierako hiriaren arabera, algoritmoak eraikitzen duen soluzioa aldatzen dela ikusten da.

Oro har, denbora laburrean soluzio onak lortzen diren arren, ausaz banatutako $n$ hirirentzat, batez beste ibilbide optimoa baino $\%25$ luzeagoak diren ibilbideak lortzen dira. Hala ere, problemaren instantzia berezi batzuetarako ibilbiderik okerrena (luzeena) itzultzen du. Problema simetrikoetan eta asimetrikoetan gerta daiteke hori.

Auzokide hurbilenaren algoritmoaren aldaerak existitzen dira. Horietako bat "zati hurbilenaren eragilea" da (ingelesez, "Nearest Fragment operator" edo "NF operator"). Aldaera horretan, bisitatuak izan ez diren hirien artean hurbil dauden hirien multzoak haien artean konektatzen dira, eta iterazioz iterazio ibilbide motzagoak aurkitzea lortzen da.

Bi algoritmoak konbina daitezke, hau da, auzokide hurbilenaren algoritmoa aplikatu soluzio bat eraikitzeko eta ondoren zati hurbilenaren eragilea aplikatu soluzio hori hobetzeko. Konplexutasun-ordenari dagokionez, $O(n^{2})$ eta $O(n^{2}{\text{log}}n)$ denboran exekutatzen dira, hurrenez hurren.

Beste heuristiko eraikitzaile bat "Match Twice and Stitch" algoritmoa da (euskaraz "Birritan Parekatu eta Josi"). Algoritmo honek hirietatik pasatzen diren ziklo multzoak sortzen ditu eta gero zikloak elkartzen ditu hiri guztietatik pasatzen den ibilbide bat osatzeko.

Christofides-Serdyukov algoritmoa

Algoritmo hau bidaiariaren problemaren instantzia berezi batzuetan soilik aplika daiteke: espazio metriko batean kokatzen diren instantzietan bakarrik, hau da, $i.$ hiria $H_{i}$ izanik, hurrengo propietateak betetzen dituzten instantzietan (informazio gehiagorako, ikus kasu berezien ebazpena):

• $\forall H_{i},H_{j},\ d(H_{i},H_{j})\geq 0\ {\text{eta}}\ d(H_{i},H_{j})=0\Longleftrightarrow H_{i}=H_{j},\ i,j=1,\dots ,n$

• $\forall H_{i},H_{j},\ d(H_{i},H_{j})=d(H_{j},H_{i}),\ i,j=1,\dots ,n$
• $\forall H_{i},H_{j},H_{k},\ \ d(H_{i},H_{j})\leq d(H_{i},H_{k})+d(H_{k},H_{j}),\ \ \ i,j=1,\dots ,n\ \ \ \rightarrow \ ({\mbox{desberdintza triangeluarra}})$

Algoritmoak kasurik okerrenean soluzio optimoa baino 1,5 aldiz luzeagoa den ibilbidea bueltatzen duela frogatu da. Hori lortzeko, grafo teoriako emaitzak erabiltzen dira. Izan ere, grafo eulertar batean zirkuitu eulertar bat aurki daiteke $O(n)$ denboran. Hortaz, saltzaile ibiltariaren instantzia batetik abiatuz grafo eulertar bat osa badaiteke (hiriak erpinak izanik), algoritmoa aplika daiteke zirkuitu eulertarra aurkitzeko, eta ondoren zirkuitutik bidaiariaren problemarako soluzioa aurkitu. Espazio metrikoaren propietateetatik erraz ondoriozta daiteke bidaiariaren problemarako soluzioa ezin dela zirkuitu eulertarra baino luzeagoa izan (desberdintza triangeluarra). Horri esker, soluziorako behe-borne bat kalkula daiteke. Christofides-Serdyukov-en algoritmoak ideia hori erabiltzen du.

Bikoteak ordezkatzea (2-opt)

Bikoteak ordezkatzearen teknika: soluzio batean bi ertz ezabatu eta beste bi ertzez ordezkatu. Irudian algoritmoaren iterazio bat ikusten da.

Bikoteak ordezkatzearen teknikak (ingelesez, "pairwise exchange" edo "2-opt") ertz bikoteak ezabatzen ditu eta deskonektatuta geratu diren zatiak beste ertz batzuen bidez konektatzen ditu, iterazioz iterazio ibilbide motzagoak eraikitzen joateko helburuarekin. Distantzia euklidestarrekin lan egitean, batezbeste Christofides-Serdyukov algoritmoak baino $\%5$ hobeak diren ibilbideak lortzen direla ikusi da. Algoritmo hau eta antzeko beste batzuk asko erabiltzen dira saltzaile ibiltariaren problemaren orokorpena den "Ibilgailuak Bideratzearen Problema" (Vehicle Routing Problem, VRP) ebazteko.

Hasierako soluzioa algoritmo irenskor batekin kalkulatzen bada, egin behar den bikoteen ordezkatze kopurua jaisten da eta algoritmoaren eraginkortasuna hobetzen da, haren konplexutasuna $O(n)$ ordenakoa izango delarik. Baina hasierako soluzioa ausaz kalkulatzen bada, algoritmoaren konplexutasuna $O(n\ {\text{log}}n)$ ordenakoa izango da. Horrela esanda, pentsa daiteke konplexutasunaren maila ez dela asko igotzen, baina algoritmoaren hasierako urratsetan, bereziki, ausaz sortutako soluzio batetik hasteak ertzak 10 aldiz gehiagotan ordezkatzea suposa dezake. 2-opt algoritmoak soluzioen atalik okerrenak (ertzen gurutzaketak dauden puntuak) sakon aztertzen dituelako gertatzen da hori.

k-koteak ordezkatzea (k-opt)

k-koteak ordezkatzearen algoritmoa edo "k-opt" bikoteak ordezkatzearen orokorpen bat da. Izan ere, bi ertz ezabatu eta zatien muturretako erpinak modu desberdinean elkartu ordez, $k$ ertz kenduz egiten da. Beraz, $k=2$ denean, k-koteak ordezkatzearen metodoa bikoteak ordezkatzearen metodo bihurtzen da. k-koteak ordezkatzeko algoritmoen artean, $k=3$ kasua da ezagunena: 3-opt. Bell laborategietan lanean ari zen Shen Lin-ek proposatu zuen 1965. urtean.

k-opt algoritmoa honakoa da:

1. Hiri guztiak behin bakarrik zeharkatzen dituen iIbilbide bat emanik, haien artean alboko ez diren $k$ ertz ezabatzen dira.
2. Deskonektatuta geratu diren ibilbidearen $k$ zatiak elkartu behar dira, ibilbide berri bat eraikiz. Ibilbidearen $k$ zatien muturretako erpinak beste ibilbide zatien muturretako erpinetara lotu behar dira ertzak gehituz, beti ere azpi-ibilbiderik sortzen ez dela ziurtatuz (ibilbide zati bereko muturreko erpinak ezin dira konektatu haien artean, azpi-ibilbidea sortuko litzatekeelako). Prozedura horrek bidaiariaren problema beste problema sinpleago batean eraldatzen du.
3. $k$ ertz kendu ondoren solte geratu diren ibilbide zatien muturretako erpin bakoitza beste $2k-2$ erpinetara konekta daiteke (guztira $2k$ erpin geratu dira zatien muturretan, eta horietako bakoitza ezin da ez bere buruarekin ezta ibilbide-zati bereko beste muturreko erpinarekin konektatu). Indar gordinaren metodoa erabil daiteke ibilbidea osatzeko konfigurazio berri optimoa aurkitzeko, hau da, erpinak konektatzeko aukera posible guztiak aztertu eta distantzia edo kosturik txikienekoarekin geratu.

Bada k-opt algoritmoaren aldaera bat, alboko diren ertzak ezabatzea onartzen duena. $k=3$ kasurako, 2-opt algoritmoarekin lortu ahal izango liratekeen soluzioak baina dezente hobeak lortzen dira, 3-opt algoritmo estandarrak suposatzen duen kostu konputazionala ekidinez (bikoteak ordezkatzearen metodoa edo 2-opt aplikatzeak suposatzen duen kostutik gertuago). Aldaera horri "bi-eta-erdi-opt" deitu ohi zaio, 2-opt eta 3-opt algoritmoen artean dagoelao, bai kostu konputazionalaren ikuspegitik eta baita lortzen diren soluzioen kalitateari dagokionez ere.

v-opt metodoa (variable-opt)

v-opt metodoan ordezkatzen den ertz kopurua finkoa izan beharrean, aldakorra da. Ibilbide motzenaren bilaketa prozesua aurrera doan neurrian, ordezkatzen den ertz kopurua handitzen da, iterazioz iterazio. Hortik datorkio metodoari "variable-opt" edo "opt-aldakor" izena. k-opt metodoaren orokorpen bat da.

Metodo honetan oinarritzen den algoritmorik ezagunena "Lin-Kernighan" izenekoa da. Shen Lin eta Brian Kernighan ikerlariek argitaratu zuten 1972an eta bidaiariaren problemarako heuristikorik fidagarriena izan zen ia 20 urtez. 80ko hamarkadaren amaieran Bell laborategietan David Johnson eta bere ikerketa taldeak algoritmoaren hobekuntzak eta aldaera konplexuagoak garatu zituen. Hobekuntza horiek egiteko tabu bilaketa eta algoritmo ebolutiboak erabili ziren. Metodo horiek "Lin-Kernighan-Johnson" izenez ezagutzen dira.

Bidaiariaren problema ebazteko ahalmen handiena duen metodo heuristikoa v-opt dela esan ohi da. Oinarrizko bertsioarekin lortzen diren emaitzak 3-opt metodoarekin lortzen direnak bezain onak direla frogatu da.

Hobekuntza ausazkotua

Metodo hauek markov kateetan oinarritzen diren algoritmo optimizatuak dira. Bilaketa lokalerako heuristikoak dituzten azpi-algoritmoak erabiltzen dituzte eta ibilbide optimora asko gerturatzen diren soluzioak aurkitzeko gai dira 700-800 hiriko instantzien ebazpenean.

Inurri-kolonien optimizazioa

Adimen Artifizialeko ikerlari Marco Dorigok bidaiariaren problema ebazteko metodo heuristiko berri bat proposatu zuen 90eko hamarkadan: Ant Colony System (ACS) edo inurri-kolonien sistema. Algoritmoak inurrien kolonien funtzionamendua simulatzen du. Inurriek beste inurrien feromonen arrastoak jarraitzen dituzte inurritegiaren eta elikagai-iturrien arteko bide motzena aurkitzeko.

Inurrien kolonien algoritmoak hirien arteko ibilbide posibleak aztertzeko hainbat inurri birtual jartzen ditu martxan. Inurriek modu probabilistikoan eta heuristiko batean oinarrituz erabakitzen dute zein izango den bisitatuko duten hurrengo hiria. Heuristiko horrek hirira iristeko dagoen distantzia eta hirira iristeko dauden ertzetan kokatu den feromona kopurua kontuan hartzen ditu. Inurriek ertzak zeharkatzean feromona uzten dute. Inurri guztiek hirien arteko ibilaldi osoa amaitzen dutenean, ibilbide motzena egin duen inurriak feromona utziko du ibilaldi osoan eta feromonen eguneratze orokor bat egiten da. Jartzen den feromona kopurua ibilbidearen distantziarekiko alderantziz proportzionala da, hau da, zenbat eta motzagoa izan egindako ibilaldiaren distantzia osoa orduan eta feromona gehiago jartzen dute ertzetan.

1) Inurriak ausazko ibilbide bat osatzen du aukera desberdinen artean, feromona arrastoak utziz. 2) Inurri bakoitza bere ibilbidea egiten ari da, utzitako feromona-kopurua ibilbidearen luzeraren araberako izanik. 3) Ibilbideen ertz batzuk beste batzuk baino feromona gehiago dute. 4) Ebaporazio-teknikak soluzio desegokiak baztertzen ditu. Yves Aubry-k sorturiko mapa.

Inurri-kolonien optimizazio-algoritmo baten aplikazioa 7 hiriko bidaiariaren problema batean. Feromonen mapako marra gorri lodiek feromona-kopurua handiagoaren presentzia adierazten dute.

Kasu bereziak

Problema metrikoa

Bidaiariaren problema metrikoan (ingelesez, delta-TSP edo Δ-TSP), hirien arteko distantziek desberdintza triangeluarra betetzen dute. Egia esan, hirien arteko distantziek desberdintasun triangeluarra betetzen duen metrika bat osatzea oso murrizketa naturala da bidaiariaren probleman. Saltzaile ibiltariaren problemaren instantzia askotan betetzen da desberdintza triangeluarra. Horrek esan nahi du, $H_{i}$ eta $H_{j}$ hiriak ertz batez konektaturik badaude, $H_{i}$-tik $H_{j}$-ra dagoen distantzia $H_{k}$ hiritik pasata dagoena baino txikiagoa dela:

$d(H_{i},H_{j})\leq d(H_{i},H_{k})+d(H_{k},H_{j})$.

Tarteko $H_{k}$ hiri batetik pasatzean, ertzak zabaldu egiten dira eta ondorioz metrika bat osatzen dute erpin multzoaren gainean. Bidaiaren problemako hiriak planoko puntu direla kontsideratzen bada, hainbat espazio metriko agertzen dira. Hona hemen hainbat adibide, puntuen arteko distantzia metrika desberdinak erabiliz neurtuta:

• Euklidestarra: puntuen arteko distantzia euklidesen distantzia da.

• Lerrozuzena (Manhattanen distantzia): puntuen arteko distantzia puntuen $x$ eta $y$ koordenatuen arteko diferentzien balio absolutuen batura da.

• Maximoaren metrika (Chebyshev distantzia): puntuen arteko distantzia puntuen $x$ eta $y$ koordenatuen arteko diferentzien balio absolutuen maximoa da.

Azken bi metrikak, adibidez, bidaiariaren problemaren aplikazio klasiko batean erabiltzen dira: zirkuitu inprimatuen fabrikazioan (ingelesez, Printed Circuit Board, PCB). Aplikazio horretan, plaka zulatu egin behar da osagaiak plakan kokatzeko eta zulagailuaren ibilbidea planifikatu behar da. “Hiriak” egin beharreko zuloak dira, beraz. Makina zulagailua Manhattanen metrika erabiliz lan egiteko diseinatzen bada, lehenengo koordenatu batean (horizontalean, adibidez) doituko ditu bere mugimenduak eta gero beste koordenatuan (bertikalean). Horrela, puntu batetik bestera mugitzeko denbora bi koordenatuetan egindako mugimenduen batura izango da. Makina zulagailua Chebyshev distantzia (maximoaren metrika) erabiliz lan egiteko diseinatzen bada, aldiz, mugimendua bi koordenatuetan aldiberean doituko da; horrela, puntu batetik bestera mugitzeko denbora bi mugimenduen (horizontalaren eta bertikalaren) arteko maximoa da (motelena).

Berez, saltzaile ibiltariaren probleman hiriak ezin dira bi aldiz bisitatu. Hala ere, hainbat aplikaziotan ez da beharrezkoa murrizketa hori ezartzea. Kasu horietan, metrikoa ez den instantzia simetriko bat instantzia metriko bihur daiteke, horrela: jatorrizko grafoa grafo oso bihurtzen da, eta jatorrizko grafoan $A$tik $B$ra joateko bide motzenaren luzera izango da $A$ eta $B$ hirien arteko ertzaren $d_{AB}$ distantzia grafo osotuan.

Bestalde, desberdintza triangeluarra betetzen duten bidaiariaren problemetan, posiblea da grafoaren zuhaitz estaltzaile minimoetan oinarritutako algoritmoak diseinatzea problema ebazteko (grafoan ziklo hamiltondarra aurkitzeko). Izan ere, zuhaitz horien hedapeneko ertzen distantzien batura bidaiariaren problemarako soluzioaren luzeraren behe-borne bat da. Kontuan izan behar da bidaiariaren ibilbide optimoan ertz bat kenduz bide Hamiltondar bat lortzen dela, hau da, zuhaitz estaltzaile minimo bat grafoan. Horrela, zuhaitz estaltzaile minimoen goi-borneak kontuan hartuz, ibilbidearen hedapenak aztertzen dituen algoritmoa diseina daiteke. Ideia horretan oinarrituz argitaratu den algoritmo bat honakoa da:

1. Grafoan zuhaitz estaltzaile minimo bat aurkitu.
2. Zuhaitzaren ertz guztiak bikoiztu, hau da zuhaitzean $u$ erpinetik $v$ erpinera ertza dagoen guztietan, $v$-tik $u$-ra doan beste ertz bat gehitu. Eragiketa horren ondorioz grafo eulertarra lortzen da.
3. Grafo eulertar horretan zirkuitu eulertar bat aurkitu. Hedapen hori zuhaitzaren hedapenaren bikoitza da.
4. Zirkuitu eulertar horretatik hasierako grafoaren ziklo hamiltondar bat lortu behar da, prozedura honi jarraituz: zirkuitu eulertarra zeharkatu, eta jada bisitatu den erpin batera iristen den bakoitzean, jauzi egin eta hurrengora joaten saiatu zirkuitu eulertarra zeharkatuz.

Froga daiteke azken urratsak funtzionatzen duela. Gainera, desberdintza triangeluarrari esker, 4. urratseko jauzi bakoitza bide laburra da, hau da, zikloaren luzera ez da handitzen. Beraz, bidaiariaren problemaren ibilbide baterako, ibilbide optimoaren bikoitza baino motzagoa da.

Christofidesen algoritmoaren diseinua antzekoa da, baina zuhaitz estaltzaile minimoa beste problema baten soluzioarekin konbinatzen da, parekatze perfektuarenarekin. Algoritmoak gehienez soluzio optimoa baino 1.5 aldiz luzeagoa den ibilaldia itzultzen du. Christofidesen algoritmoa hurbilketa-algoritmoen artean sortu zen lehenetarikoa izan zen. Gertakaria garrantzitsua izan zen, ebazten zailak ziren problemetarako ikuspuntu desberdin bat proposatzen zelako: soluzio optimoa bermatu ordez, hurbilketa on bat lortzea zen helburua. Hasiera batean, Christofidesen algoritmoari Christofidesen heuristikoa esaten zitzaion, "algoritmo" terminoa ez zelako hurbilketa algoritmoetarako erabiltzen.

Problema Euklidestarra

Bidaiariaren problema Euklidestarra edo laua Euklidesen distantzian oinarritzen da. Bidaiariaren problema metrikoaren kasu partikular bat da, distantziak planoan desberdintza triangeluarra betetzen baitu.

Problema orokorra bezala, hau ere NP-gogorra da. Metrika diskretura bihurtutako problema (distantzia zenbaki oso bihurtzea gora biribilduz) NP-osoa da. Hala ere, problema metriko orokorra baino errazagoa da. Adibidez, bidaiariaren problema euklidestarraren instantzia bati dagokion zuhaitz estaltzaile minimoa euklidestarra da eta O (n log n) ordenakoko denboran kalkula daiteke, n izanik hiri kopurua.

Problema asimetrikoa

Kasu gehienetan, hirien arteko distantzia ez da aldatzen noranzkoaren arabera, baina batzuetan $A$-tik $B$-rako distantzia eta $B$-tik $A$-rako distantzia ez da berdina. Problema horiek asimetrikoak direla esaten da. Halako problemen aplikazio praktiko bat "Ibilgailuak Bideratzearen Problema" da (Vehicle Routing Problem, VRP), noranzko bakarrean zeharka daitezkeen kaleak daudenean. Problema asimetrikoak ebaztea zaila izan daitekeenez, aukera bat simetriko bihurtzea da, n tamainako matrize asimetriko batetik 2n tamainako matrize simetriko bat lortuz.

Izan bedi $A$, $B$ eta $C$ puntuen arteko distantziak jasotzen dituen honako 3 × 3 tamainako matrizea. Matrizeak adierazten duen grafo zuzenduan bi ziklo hamiltondar daude (bi ibilbide posible bidaiariarentzat): $\mathrm {A\to B\to C\to A}$ (9ko distantzia) eta $\mathrm {A\to C\to B\to A}$ (12ko distantzia).

Matrize asimetrikoa

	A	B	C
A		1	2
B	6		3
C	5	4

Matrizearen errenkada eta zutabe kopurua bikoizten da, puntu bakoitzarentzat beste puntu "mamu" bat sortuz, $A$ puntuarentzat $A'$ puntu mamua, adibidez. Puntuen eta puntu mamuen arteko distantziari oso balio baxua esleitzen zaie (adibidean −∞), puntu mamu guztiak soluzio optimoan ager daitezen. Jatorrizko matrize asimetrikoa matrize bikoiztuaren behealdeko ezkerreko zatian ikusten da (diagonalean −∞ balioekin), eta matrizea bera baina diagonal nagusiarekiko iraulita goialdeko eskuineko zatian (hau ere bere diagonalean −∞ duelarik). Matrize berrian jatorrizko $A$, $B$ eta $C$ puntuen artean ez dago ertz bidezko konexio zuzenik, ezta $A'$, $B'$ eta $C'$ puntu mamuen artean ere. Erraz ikus daiteke matrize berria simetrikoa dela diagonal nagusiarekiko.

Matrize simetrikoa

	A	B	C	A′	B′	C′
A				−∞	6	5
B				1	−∞	4
C				2	3	−∞
A′	−∞	1	2
B′	6	−∞	3
C′	5	4	−∞

6 × 6 tamainako matrizeak adierazten duen grafo zuzenduan honako ziklo hamiltondarra existitzen da: $\mathrm {A\to A'\to B\to B'\to C\to C'\to A}$. Ikusten den bezala, ibilbidean puntu batetik dagokion puntu mamura joaten da, hau da, $A$, $B$, $C$ puntuak eta horien puntu mamu diren $A'$, $B'$, $C'$ puntuak txandakatzen dira. $\mathrm {A\to A'}$ moduko bikoteetan "jauzi" egiten da, distantzia zero dela interpreta daitekeelako. Horrela, $\mathrm {A\to A'\to B\to B'\to C\to C'\to A}$ zikloa $\mathrm {A\to B\to C\to A}$ bihurtuko da (9ko distantziakoa).

Konplexutasun konputazionala

Saltzaile ibiltariaren problema NP-gogorra dela frogatu da (zehatzago esanda, NP-osoa da FP^NP konplexutasun-klaserako; ikus funtzioaren problema), eta problemaren honako bertsioa NP-osoa da: distantzien matrize bat eta $x$ zenbaki bat emanik, erabaki $x$ distantzia baino txikiagoa den ibilbidea existitzen den. "Bidaiariaren Problema Botila-lepoduna" (ingelesez, Bottleneck TSP) ere NP-gogorra da. Problemak NP-gogor izaten jarraitzen du hirien arteko distantziak planoan distantzia euklidestarra erabiliz kalkulatzen badira ere. Problemaren planteamendutik hiri bakoitza "behin bakarrik" bisitatzeko eskakizuna kenduta ere problemak NP-gogor izaten jarraitzen du.

Hurbiltze-algoritmoen konplexutasuna

Problemaren planteamendu orokorra, hau da, hiri guztiak behin bakarrik bisitatu eta hasierako hirian amaitzen den ibilbiderik laburrena aurkitzea, NPO-osoa da (NP-Optimization problem, NPO). Distantziaren neurria metrika bada (eta, beraz, simetrikoa), problema APX-oso bihurtzen da (ingelesez, APproXimable-complete), hau da, NP optimizazio problema da baina konstante batez mugatutako hurbilketa bat kalkulatzea posiblea da hurbilketa-algoritmo baten bidez denbora polinomialean. Christofidesen algoritmoak gehienez ibilbide laburrena baino 1.5 aldiz luzeagoa den ibilaldia itzultzen du.

Distantziak 1era eta 2ra mugatzen badira (metrika bat izanik), hurbilketa-ratioa 8/7-ekoa bihurtzen da, hau da gehienez 8/7 aldiz luzeagoa den ibilaldia aurkitzen da. Desberdintza triangeluarra betetzen duten problema asimetrikoetan, duela gutxira arte emaitza denbora logaritmikoan itzultzen zuten algoritmoak besterik ez ziren ezagutzen. 2018an, Svensson-ek, Tarnawski-k eta Végh-ek faktore konstante bateko hurbilketa metodoa garatu zuten. Gaur egungo algoritmo onena Traub-ek eta Vygen-ek garatu zutena da, $22+\varepsilon$ errendimendua lortzen du. Ezagutzen den hurbiltasunerako bornerik onena 75/74-koa da.

Bidaiariaren problemaren maximizatze-bertsiorako, hau da, hiri guztiak behin bakarrik bisitatu eta hasierako hirian amaitzen den ibilbiderik luzeena aurkitzearen problemarako, soluzioa 63/38-an hurbil daiteke. Distantziaren funtzioa simetrikoa bada, algoritmo determinista bat erabiliz ibilbide luzeena 4/3-ean hurbil daiteke eta ausazkotasuna erabiltzen duen algoritmo baten bidez ${\tfrac {1}{25}}(33+\varepsilon )$ -ean.

Gizakien eta animalien errendimendua

Bidaiariaren problemaren ebazpenak psikologia kognitiboko ikertzaileen arreta erakarri du. Izan ere, gizakia problemaren soluziotik oso gertu dauden ibilbideak azkar (ia denbora linealean) aurkitzeko gai dela ikusi da. Hiri kopuruaren arabera errendimendua aldatzen da: 10-20 hiriko problemetan (10-20 erpin dituzten grafoetan) aurkitutako ibilbidea optimotik %1 aldendu daiteke eta problema handiagoetan (120 erpineko grafoetan) %11. Gizakiek problema ebazteko eta optimotik gertu dauden soluzioak erraz (itxuraz behintzat) aurkitzeko erakutsi duten ahalmenak ikertzaileak hipotesiak egitera eraman ditu. Hipotesi horietako batek dio, gizakiek heuristikoak erabiltzen ditutela. Horren inguruko teoriarik ezagunenak ganbiltasunaren hipotesia (ingelesez, convex-hull hypothesis) eta gurutzatzea saihestearen heuristikoa (ingelesez, crossing-avoidance heuristic) dira. Hala ere, giza errendimendua askotarikoa dela ikusi da, gizaki batzuek trebetasun handia erakusten duten arren beste batzuek traketsak dira soluzio onak aurkitzen. Gainera, grafoaren geometriak ere eragin handia sortzen du problemaren ebazpenaren errendimenduan. Gizakiek erabiltzen dituzten estrategiak ulertu eta emulatuz gero, bidaiariaren problema ebazteko algoritmo hobeak aurkitu ahal izango direla ondorioztatu da egindako ikerketetatik. Horrekin batera, giza pentsamenduaren mekanismoak hobeto ezagutzea lortu da. "Journal of Problem Solving" aldizkari zientifikoaren lehen alea bidaiariaren problemaren ebazpenean gizakiek erakutsitako errendimenduari buruzkoa izan zen, eta 2011ko argitalpen batean gaiari buruzko dozenaka artikulu zientifiko zerrendatzen dira.

2011ean animalien kognizioari buruzko ikerketa bat egin zen. Ikerketaren izenburua "Let the Pigeon Drive the Bus" zen, euskaraz "Utzi usoari autobusa gidatzen". "Don't let the Pigeon Drive the Bus!" haurrentzako liburu ezagunaren izenburutik abiatuz jarri zitzaion izen hori ikerketa proiektuari. Helburua usoek espazioari buruz duten ezagutza aztertzea zen. Haien hegaldi-ereduak aztertu nahi zituzten, bidaiariaren problemaren ebazpenerako estrategia berriak bilatzeko asmoz. Horretarako, laborategi batean txorientzako hainbat elikagailu jarri zituzten ilarrekin. Hasierako esperimentuan, usoak laborategiko txoko batean kokatu eta aske utzi zituzten, elikagailuetako ilarrak jatera joan zitezen. Ikertzaileek ikusi zuten usoak hurbilen zegoen elikatzailera joaten zirela, gehienetan. Bigarren esperimentuan ez zuten ilar kopuru bera jarri elikagailu guztietan, gertuen zeudenetan oso gutxi jarri zuten eta urrutiago zeudenetan gehiago. Usoak askatzean, haiek egindako hegaldiak aztertuz konturatu ziren hurbilen zegoen elikagailura joateak elikagailu guztiak bisitatu behar izatea eragiten zuen kasuetan, usoek haien jokaera aldatzen zutela. Horrela, usoek nora joan erabaki behar zutenean hurbil egoteak garrantzia bazuela ikusi zuten arren, haien hegaldia hainbat urratsetan planifikatzeko gai zirela ondorioztatu zuten eta batzuetan urrunago dagoen elikagailura joatea erabakitzen zutela. Hori horrela egiten zuten, batez ere beti hurbilenera joatea eraginkorra ez zenean (ilar gutxi zegoenean hurbilenekoetan). Emaitza horiek bat datoz primateak ez diren beste animalia batzuekin egindako esperimentuetako emaitzekin, eta frogatzen dute primateak ez diren animalia batzuek gai direla ibilbide konplexuak planifikatzeko. Hortaz, badirudi primate ez diren animaliek espazioa kudeatzeko trebetasun kognitibo sofistikatu samarra izan dezaketela.

Konputazio naturala

Badira naturan inspiratuta garatu izan diren ebazpen metodoak. Bidaiariaren problema euklidestarrerako hurbilpen soluzio bat aurkitzeko, adibidez, partikulen populazio bat difusio-sare batean zehar mugitzean materialaren portaera morfologikoa nola egokitzen den aztertu izan da. Ikerketa lan batean Physarum polycephalum motako ameba hainbat puntuz (elikadura-iturriz) osatutako sare batean kokatu zuten, eta ikusi zen ameba tamainaz txikitzen zela elikadura-puntuen konfiguraziora egokituz zioan neurrian. Eskuz amebaren perimetroa jarraituz gero, elikadura-puntuen arteko ibilbide bat aurkitu ahal izango litzateke. Ibilbide hori saltzaile ibiltariaren problemarako soluzio optimoaren hurbilpen moduan ikus daiteke.

Algoritmoen ebaluazioa

Bidaiariaren problema ebazteko algoritmoak ebaluatzeko, badira liburutegi estandarrak. . TSPLIB liburutegian hainbat adibideren instantziak eta erlazionatutako problemak aurki daitezke (ikus TSPLIB kanpo erreferentzien atalean) Instantzia horietako asko egungo hirien zerrendak eta gaur egungo zirkuitu inprimatuen diseinuak dira.

Kulturan eta zineman

• "Travelling Salesman" Timothy Lanzone-k 2012an zuzendutako filma da. Ameriketako Estatu Batuetako gobernuak kontratatutako lau matematikariren istorioa kontatzen da. Informatikaren historiako problemarik zailena ebazteko kontratatuak izan dira: P vs NP problema ebazteko

• Bob Bosch matematikariak eta Tom Wexler informatikariak bidaiariaren problemaren soluzioak erabiltzen dituzte artelanak puntuen eta haietatik pasatzen diren ibilbideen bidez adierazteko. "Optimization art" edo "opt-art" deitzen zaio teknika horri.

Ikus, gainera

• Postari txinatarraren ebazkizun
• Königsbergeko zazpi zubietako ebazkizuna

Kanpo estekak

• Datuak: Q322212
• Multimedia: Traveling salesman problem / Q322212