Toru

Torua

Geometrian, torua (latinezko torus hitzetik) biraketa-gainazal bat da, zirkunferentzia batek haren plano berean dagoen zuzen baten inguruan bira egitean sortzen duena. Hitz arruntagoetan, esan liteke pneumatiko baten aire-ganberaren forma duela toruak. Toroidearen kasu berezi bat da.

Zuzenak (errotazio-ardatza) zirkunferentzia ukitzen edo ebakitzen ez badu, toruak hutsune bat du erdian, eta eraztun baten antza du. Bestela, errotazio-ardatza zirkunferentziaren korda bat bada, esfera zapal baten antzeko zerbait sortzen da, kuxin biribil baten itxurakoa; are gehiago: esfera toruaren kasu berezi bat da, errotazio-ardatza zirkunferentziaren diametro bat denean.

Definizio orokorrago baten arabera, toruaren sortzailea, zirkunferentzia bat ez ezik, elipse bat edo beste kurba koniko bat ere izan daiteke.

Ekuazioak

Toru baten adierazpide diedrikoa

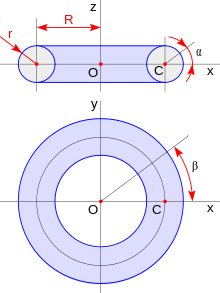
Toruaren ekuazio parametrikoak hauek dira:

$x(u,v)=(R+r\cos {v})\cos {u}\,$

$y(u,v)=(R+r\cos {v})\sin {u}\,$

$z(u,v)=r\sin {v}\,$

non

u, v ∈ [0, 2π],

R zirkunferentziaren zentrotik zuzenerainoko (toruaren zentroa) distantzia, eta

r zirkunferentziaren erradioa (hodiaren erradioa) diren.

(R eta r bi distantziek erradio handia eta erradio txikia izenak ere hartzen dituzte, hurrenez hurren)

OZ ardatzarekiko azimutalki simetrikoa den kasuan, toruak ekuazio hau du koordenatu kartesiarretan:

$\left(R-{\sqrt {x^{2}+y^{2}}}\right)^{2}+z^{2}=r^{2}$

Toruaren azalera eta barneko bolumena formula hauen bidez kalkulatzen dira:

$A=4\pi ^{2}Rr=\left(2\pi r\right)\left(2\pi R\right)\,$

$V=2\pi ^{2}Rr^{2}=\left(\pi r^{2}\right)\left(2\pi R\right).\,$

Kanpo estekak

• (Ingelesez) Weisstein, Eric W.: "Torus" MathWorld-en.
• (Ingelesez) More Torus Images

• Datuak: Q12510
• Multimedia: Torus / Q12510