Bektore (matematika)

Matematikan, bektoreak (v1, v2,...,vn) zenbakien n-kote bat da orokorrean, maiz bektore espazio bateko elementu gisa aztertzen dena. Geometrikoki ere defini daiteke: adiera sinplean, puntu batetik punturako zuzenki bideratua da, adierazten dena; hortik, era orokorrean, bektorea norma edo luzera, norabidea eta noranzkoa dituen v objektu geometriko bat dela esan daiteke, edo (azken hau letra lodiaz idatzirik).
Bektoreak zuzenki bideratu moduan: bektore finkoak eta bektore askeak[aldatu | aldatu iturburu kodea]

Bitez eta bi puntu, planoan do hiru edo dimentsio handiagoko espazio batean. tik (jatorri deituko den puntutik) ra (helmuga deituko den puntura) doan zuzenki bideratua edo bektore finkoa da. Kokapen-bektorea koordenatu-sistema bateko jatorria (esaterako, (0,0) puntua planoan) puntu batekin lotzen duena da; honela adierazten da: .
Bi zuzenki bideratu luzera, norabide eta noranzko berdinak dituztenean, ekipolenteak edo berdinak direla esaten da. Elkarrekin ekipolenteak diren bektoreen multzoa bektore aske bat dela esaten da, eta luzera, norabide eta noranzko berdinarekin definitzen den bektore bat da, jatorriko eta helmugako puntua gorabehera.
Bektore aske baten koordenatuak kalkulatzeko, helmugako puntuaren koordenatuak ken jatorriko puntuaren koordenatuak egin behar da. Adibidez, A(2,3) eta B(9,6) puntuak izanik, bektore finkoari dagokion bektore askearen koordenatuak honela kalkulatzen dira: . Noski, beste hainbat bektore finko (infinitu, zehatzago) daude bektore aske berdina sortzen dutenak; esaterako C(4,5) eta D(11,8) puntuak izanik, bektoreari dagokion bektore askearen koordenatuak dira. eta bektoreak ekipolenteak dira, beraz.
Koordenatuen arabera[aldatu | aldatu iturburu kodea]

Bektorea erreferentzia sistemaren arabera idatzi behar da, hau definitzen duten koordenatuen konbinazio lineal modura. Horretarako koordenatu horien norabideko bektore unitarioen (modulua bat baliokoa daukatenak) konbinazio lineal bezala idazten da.
Orokorrean, X,Y eta Zren koordenatu sistema kartesiarra erabiltzen bada ko edozein bektore idatz daiteke , eta bektoreen konbinazio lineal bezala. Hauen balioak , eta baitira hurrenez hurren. Adibidez, .
Ohikoena koordenatu kartesiarretan adieraztea den arren, bektoreak beste koordenatu sistema batzuen arabera ere idaz daitezke, zeinahi bektore independiente sorta oinarritzat dutenak. Bektorearen adierazpena erreferentzia sistema batetik bestera aldatzeko eragiketa algebraiko batzuk egitea nahikoa izan ohi da.
Horrez gain, badira beste zenbait adierazpen berezi ere, koordenatu zilindrikoak edo koordenatu esferikoak kasu. Hauetan bektorearen luzera eta angelua erabil daitezke, adibidez, bektorea adierazteko. Beste koordenatu mota batetan idazteko beharrezko aldaketa formulak baino ez dira aplikatu behar.
Bektoreekin eragiketak[aldatu | aldatu iturburu kodea]
Bektoreen arteko konbinazio lineala[aldatu | aldatu iturburu kodea]
Bektoreen artean konbinazio linealak eginez beste bektore batzuk sortzen dira.
Batuketa[aldatu | aldatu iturburu kodea]
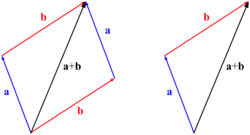
Bektoreen arteko batuketa grafikoki edo analitikoki egin daiteke. Batura beti izango da beste bektore bat, inoiz ez eskalarea.
Grafikoki eskumako marrazkian adierazten bezala egiten da, bigarren bektorearen jatorria lehenengoaren puntan kokatzen da. Batura definitzen duen bektorea lehenengoaren jatorritik doana bigarrenaren puntaraino doana izango da. Bi bektore hauek edozein izanda ordenak ez dauka garrantzirik grafikoan ikus daitekeenez. Era honetan, bi bektore baino gehiago ere batu daitezke hirugarrenaren jatorria bigarrenaren puntan kokatuz etab.
Analitikoki batu ahal izateko oinarri jakin batean bektoreen koordenatuak ezagutu behar ditugu. Ondoren, koordenatuen balioak banan batu baino ez dira egin behar. Hiru dimentsiotako oinarri kanonikoan 2 bektore batzen badira:
Era honetan ere bi bektore baino gehiago batu daitezke aldi berean. n bektore kontsideratzen badira:
Kenketa[aldatu | aldatu iturburu kodea]

Era grafikoan egiteko nahikoa da bi bektoreen jatorrian elkarrekin kokatzea eta hirugarren bektore bat sortzea lehenengoaren puntatik bigarrenaren puntaraino. Ordena, beraz aldaezina da eta kenketa bi angelurekin kalkulatu behar da.
Era analitikoan egiteko modurik egokiena adieraztea da, eta aurretik ikusitako garapena egitea..
Eskalar batekin biderkaketa[aldatu | aldatu iturburu kodea]
Eskalar eta bektoreen arteko biderkadurak ere bektoreak dira. Bektore berri hauek aurrekoaren paraleloak izango dira, baina norma eskalarearen balioarekin biderkatuko da. Adibidez:
Norma aldiz handituko dela frogatzeko:
Beraz,
Konbinazio lineala[aldatu | aldatu iturburu kodea]
Egia esan, aurreko bi kontzeptuak konbinazio linealaren kasu orokorrak dira, baina askotan agertzen dira bakarrik.
Bektore bat beste batzuen konbinazio lineala dela esaten da bektore hauek guztiak zero ez diren eskalar banarekiko biderkatzerakoan eta haien artean batzerakoan bektore hori emaitza daukatenean:
bada bektorea guztien konbinazio lineala da.
Konbinazio linealak, eragiketa bera egiteaz gain, bektore-sistema libreak topatzeko ere balio du. Bektore sistema libreek ez daukate konbinazio linealik bere baitan; hau da, sistemako bektore bat ere ezin da besteen konbinazio lineal bezala adierazi. Bektore-sistema ez libreei lotuak deitzen zaie.
Bektoreen arteko biderkadura[aldatu | aldatu iturburu kodea]
Biderkadura eskalarra[aldatu | aldatu iturburu kodea]
Biderkadura eskalarra bektore bat bere gain proiektaturiko beste bektore batekin biderkatzean datza, eta emaitza zenbaki eskalarra da. Bi bektoreen normak eta haien arteko angeluaren kosinua biderkatuz lor daieke:
Biderkadura bektoriala[aldatu | aldatu iturburu kodea]
Biderkadura bektorialaren emaitza beste bektore bat da, zeina biderkaturiko bi bektoreek sorturiko planoari perpendikularra den, eta bere normak bektoreek sorturiko paralelepipedoaren azaleraren balioa duen. Bektoreen normak eta haien arteko angeluaren sinua biderkatuz biderkaduraren norma lor daiteke:
Deribatuak[aldatu | aldatu iturburu kodea]
Deribatu arrunta[aldatu | aldatu iturburu kodea]
Funtzio bektorial baten deribatu arrunta, dimentsio bakoitzean funtzioa deribatuz lortzen da. Adibidez, a(t) funtzio bektoriala hartuz:
Deribatu arrunta honakoa litzateke:
Deribatu kobariantea[aldatu | aldatu iturburu kodea]
Erreferentzia sistema mugikor baten kasuan, deribatua kalkulatzeko funtzioaren aldaketaz gain erreferentzia sistemaren aldaketa ere kontuan hartu behar da. Kasu horietan erabiltzen da deribatu kobariantea, eta a(t) funtzio bektorial batentzat honako itxura du:
Normaren kalkulua[aldatu | aldatu iturburu kodea]
Bi bektoreen arteko angeluaren kalkulua[aldatu | aldatu iturburu kodea]
eta jakinda,bektore hauek sortzen duten angelua kalkulatu daiteke biderketa eskalarraren ekuaziotik abiatuz. Horrela geratuko zlitzateke:
Bektoreen biderketa eskalarra zati beraien moduloak eginez lortzen dugu eta arkokosinua (arcocoseno) eginez angelua lortuko dugu.






































