Banaketa uniforme jarraitu
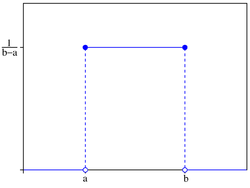
Probabilitate teorian eta estatistikan, banaketa uniforme jarraitua dentsitate-funtzio konstante bati jarraitzen dion X zorizko aldagairen probabilitate banaketa da:
Banakuntza uniforme jarraituak bi parametro ditu: a eta b. Labur, honela adierazten da X zorizko aldagaiak banaketa uniforme jarraituari jarraitzen diola, a eta b parametroak dituela:
Ezaugarriak[aldatu | aldatu iturburu kodea]
Banakuntza uniforme jarraituaren itxaropena eta bariantza hauek dira hurrenez hurren:
Erabilera[aldatu | aldatu iturburu kodea]
Banakuntza uniforme jarraituak probabilitate berdintasuna ezartzen du zorizko aldagaiak har ditzakeen balio guztietan, tarte osoan zehar. Horrela, zorizko aldagai bati buruz suertatu den balioari buruzko erabateko ziurgabetasuna dagoenean, tarte batean probabilitate handiagoz edo txikiagoz izango den ezarri ezin delarik, erabiltzen da.



![{\displaystyle \mu =E[X]={\frac {a+b}{2}}\ \ ;\ \ \sigma ^{2}=var[X]={\frac {(b-a)^{2}}{12}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b99f7d1e132dfce4a0ad4b785578178ca728ecb4)