Clarke eta Parken transformatuak

Clarke eta Parken transformatuak erreferentzi sistemeen aldaketetan oinarritzen diren eragiketa matematikoak dira. Transformatu hauek, gehienbat, potentziazko elektronikako kontrol arloan erabiltzen dira; abiadura zehatz batean aldatzen diren balioak, balio konstanteak bihurtu ditzaketelako.

Autoreak

Clarke

Edith Clarke 1883ko otsailaren 10ean jaio zen Ellicott izeneko herrian. John Ridgely Clarkek eta Susan Dorsey Owingsek izan zituzten bederatzi seme-alabetako bat izan zen. 1908. urtean Vassar Collegen matematika eta astronomiako ikasketak bukatu zituen, herentziako diruari esker. Ingeniaritza zibila eta elektrikoarekin jarraitu zituen bere ikasketak eta 1919an bihurtu zen MITeko ingeniari elektrikoa M.S.-a irabazten zuen lehenengo emakumean. Bere bizitzan lan matematiko desberdinak gauzatu zituen, baina haien arteko garrantzitsuenetako bat 1926an Clarkeren ekuazioak izenarekin garatutakoa da. Clarke 1959ko urriaren 29an hil zen, 76 urterekin.

Park

Robert H. Park 1902an jaio zen, Estrasburgon. Haren aita, Robert Ezra Park, soziologoa, ikertzailea eta irakaslea izan zen, Heidelbergeko Unibertsitatean. Roberthek 1923an Massachusettseko Institutu Teknologikoan graduatua lortu zuen. Alemaniako ingeniari elektriko ospetsu haren interesgune nagusia, nahiz eta pentsalari originala izan eta hainbat arlotan lan egin, elektronikan eta motorren diseinua izan zen beti. Robert H. Park gogoratua da potentziazko elektronikoen eta makinen diseinatzaileen artean, 1929an Amerikako ingeniaritza elektronikako institutuan idatzitako dokumentuagatik; hau da, Parken ekuazioengatik.

Aplikazio arloa

Transformatu hauei esker, PI erresonanteak PI arruntekin ordezka daitezke, sintonizazio arazoak ekiditeko; izan ere, aldagai konstanteak lortzen direnez, erregimen permanenteko errorea anula daiteke. PI erresonanteak sintonizatzeko arazoak uler daitezke kontrolaren bodea begiratuz, ikus daitekeen moduan oso frekuentzia tarte txikian ganantzia handia daukatelako, baina beste frekuentzientzat filtro edo iragazki gisa lan egiten dutelako. Hortaz, oso garrantzitsua da ganantzia handiko frekuentzia ondo zehaztea, eta hori askotan prozesu zaila izan daiteke.

PI erresonantearen Bodea

Transformatuen aplikazio tipiko bat motorren kontrola da.

Motor baten kontrola, transformatuak erabiliz

Transformatuak aplikatzeko metodoa

Clarkeren transformatua

Sistema trifasiko baten errepresentazioa bektore espazial baten bidez

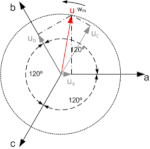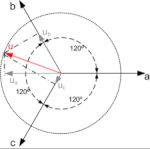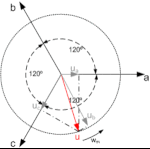
Sistema trifasiko baten fase bakoitzeko uneko balioak bektore espazial baten bidez irudika daitezke, bektoreak ardatz bakoitzean daukan proiekzioen bidez. Proiekzio horiek ondorengo matrize honen bidez irudika daitezke:

$U_{abc}=\mathbf {\begin{bmatrix}U_{a}\\U_{b}\\U_{c}\\\end{bmatrix}} =U_{abc}\cdot \mathbf {\begin{bmatrix}\cos(\theta )\\\cos(\theta +{\frac {2\pi }{3}})\\\cos(\theta -{\frac {2\pi }{3}})\\\end{bmatrix}}$

Clarkeren transformatuak proposatzen du aurreko matrizean agertzen diren ekuazioen sinplifikazioa; horretarako, hurrengo formulen bidez, sistema trifasikoaren errepresentazioa hiru ardatzeko (abc) proiekzioa daukan bektore espazial baten bidez egin beharrean, bi ardatzetan (αß) egiten da. Aldaketa horri esker, sistema elektrikoen analisia asko errazten da hiru ekuazio izan beharrean bi ditugulako.

Clarkeren trasnsformatua

$U_{\alpha \beta \gamma }=\mathbf {\begin{bmatrix}U_{\alpha }\\U_{\beta }\\U_{\gamma }\\\end{bmatrix}} ={\begin{bmatrix}T\\\end{bmatrix}}\cdot \mathbf {\begin{bmatrix}U_{a}\\U_{b}\\U_{c}\\\end{bmatrix}}$

Non

${\begin{bmatrix}T\\\end{bmatrix}}={\frac {2}{3}}\cdot \mathbf {\begin{bmatrix}1&-1/2&-1/2\\0&{\sqrt {3}}/2&-{\sqrt {3}}/2\\1/2&1/2&1/2\\\end{bmatrix}}$

Kalkuluak inbertitu ahal izateko, matrizearen antitransformatua behar da.

Clarkeren antitrasnsformatua

$U_{abc}=\mathbf {\begin{bmatrix}U_{a}\\U_{b}\\U_{c}\\\end{bmatrix}} ={\begin{bmatrix}T\\\end{bmatrix}}^{-1}\cdot \mathbf {\begin{bmatrix}U_{\alpha }\\U_{\beta }\\U_{\gamma }\\\end{bmatrix}}$

Non

${\begin{bmatrix}T\\\end{bmatrix}}^{-1}=\mathbf {\begin{bmatrix}1&0&1\\-1/2&{\sqrt {3}}/2&1\\-1/2&-{\sqrt {3}}/2&1\\\end{bmatrix}}$

Parken transformatua

Parken trasnsformatua

Clarkek garatutako ekuazioen aplikazioari esker, kontrola bi aldagaitara murritz daiteke, baina, oraindik, PI erresonanteen beharra dago (αß) ardatzak finkoak diren bitartean, ${\vec {u}}$ bektorea mugitzen delako. Arazo hau ekidin ahal izateko, Parkek ardatz finkoak ${\vec {u}}$ bektorearen abiaduran mugitzen diren ardatzetan bihurtzea planteatu zuen hurrengo matrizeei esker.

$U_{dq0}=\mathbf {\begin{bmatrix}U_{d}\\U_{q}\\U_{o}\\\end{bmatrix}} ={\begin{bmatrix}A\\\end{bmatrix}}\cdot \mathbf {\begin{bmatrix}U_{a}\\U_{b}\\U_{c}\\\end{bmatrix}}$

Non

${\begin{bmatrix}A\\\end{bmatrix}}={\frac {2}{3}}\cdot \mathbf {\begin{bmatrix}\cos(\theta )&\cos(\theta -{\frac {2\pi }{3}})&\cos(\theta +{\frac {2\pi }{3}})\\-\sin(\theta )&-\sin(\theta -{\frac {2\pi }{3}})&-\sin(\theta +{\frac {2\pi }{3}})\\1/2&1/2&1/2\\\end{bmatrix}}$

Aldagaiak hasierako sistema trifasikora bueltatzeko, hurrengo matrize hau erabili behar da:

$U_{abc}=\mathbf {\begin{bmatrix}U_{a}\\U_{b}\\U_{c}\\\end{bmatrix}} ={\begin{bmatrix}A\\\end{bmatrix}}^{-1}\cdot \mathbf {\begin{bmatrix}U_{d}\\U_{q}\\U_{o}\\\end{bmatrix}}$

Non

${\begin{bmatrix}A\\\end{bmatrix}}^{-1}=\mathbf {\begin{bmatrix}\cos(\theta )&-\sin(\theta )&1\\\cos(\theta -{\frac {2\pi }{3}})&-\sin(\theta -{\frac {2\pi }{3}})&1\\\cos(\theta +{\frac {2\pi }{3}})&-\sin(\theta +{\frac {2\pi }{3}})&1\\\end{bmatrix}}$

Bibliografia

• E. Clarke, “Circuit Analysis of AC Power Systems”. New York: Wiley, 1950, vol. I
• Gonzalo Abad; Jesús López; Miguel A. Rodríguez; Luis Marroyo; Grzegorz Iwanski. (2011).Doubly fed induction machine: modeling and control for wind energy generation applications. Mohamed E. El-Hawary. ISBN 978-0-470-76865-5

Kanpo estekak

• Francisco M. Gonzalez-Longatt-en artikulua, Parken transformatuei buruz
• Matlab-eko laguntza orria, Clarke eta Parken transformatuei buruz

• Datuak: Q30634
• Multimedia: Dqo transform / Q30634