Wheatstone zubia
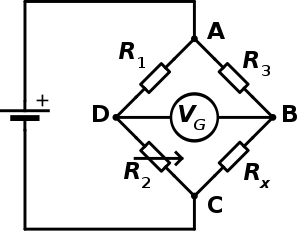
Wheatstone zubia, Samuel Hunter Chirstie 1833. urtean asmatu eta Sir Charles Wheatstone 1843. urtean hobetu eta sustatutako, neurtzeko gailu bat da. Erresistentzia ezezagunak neurtzeko erabiltzen da zubi zirkuitu baten bi adarrak orekatuz, non adar batek osagai ezezaguna duen.( Bere funtzionamendua jatorrizko potentziometroaren antzekoa da).
Funtzionamendua[aldatu | aldatu iturburu kodea]
neurtu behar den erresistentzia ezezaguna da; , eta balio ezaguneko erresistentziak dira eta aldakorra da. Ezagutzen den adarreko bi erresistentzien arteko erlazioa eta ezagutzen ez den adarreko erresistentzien arteko erlazioa berdina bada, orduan tarteko puntuen arteko (B eta D) tentsioa 0 izango da eta galvanometrotik ez da korronterik pasako. aldatu egiten da baldintza hau lortu arte. Korrontearen norantza altuegia edo baxuegia den adierazten du.
Zero balioko korrontea zehaztasun haundiarekin egin daiteke (galvanometroen bidez). Beraz, , eta zehaztasun haundiarekin ezagutzen baldin badira, zehaztasun haundiarekin neurtu daiteke. ko aldaketa oso txikiak ere oreka desgiten dute eta detektatu egiten dira.
Oreka puntuan, ratioak
Beraz,
Beste aldetik, , , eta ezagunak badira, baina ez da aldakorra, Kirchhoffen legeak erabiliz, tentsio diferentzia edo neurgailutik pasatzen den korrontea RXen balio kalkulatzeko erabil daitezke. Modu hau oso erabilia da galga extensiometriko eta erresistentzia termometroetan, azkarrago izaten baita normalean neurgailu bateko tentsio balio bat irakurtzea resistentzia bat 0 tentsioara mugitzea baino.
Kalkuluak[aldatu | aldatu iturburu kodea]
Hasteko, Kirchhoffen lehenengo legea erabiltzen da B eta D nodoetan korronteak aurkitzeko:
Gero, Kirchhoffen bigarren legea erabiltzen da ABD eta BCD mailetan tentsioa aurkitzeko.:
Zubia orekatua dago eta , beraz bigarren ekuazio taldea honela berridatz daiteke:
Gero, ekauazioak zatitzen dira eta birodenatu eta gero hurrengoa ematen dute:
Lehenengo legetik, eta . Orain balioa ezaguna da, honela adierazita:
Lau erresistentziak eta jatorrizko tentsioa ezagunak badira, zubian zeharko tentsioa aurki daiteke potentzial zatitzaile bakoitzeko tentsioa kalkulatuz eta bien arteko kenketa eginez. Honetarako ekuazioa:
Sinplifika daiteke:
Garrantzia[aldatu | aldatu iturburu kodea]
Wheatstone zubiak, oso zehatza izan daitekeen, diferentzia neurketaren kontzeptuak argitzen du. Wheatstone zubiaren eraldaketak kapazitantzia, induktantzia, inpedantzia eta bestelako kantitateak neurtzeko erabil daiteke, adibidez lagin batean dauden gas erretzaileak (eztandametroa). Kelvinen zubi bikoitza Wheatstone zubitik bereziki moldatu zen oso erresistentzia baxuak neurtzeko. Kasu askotan, erresistentzia ezezagunaren neurketaren garrantzia bestelako fenomeno fisiko baten eragina neurtzeko erabiltzean datza (tenperatura. Presioa, etab.), wheatstone zubiak elementu horiek modu ez zuzenean neurtzea ahalbidetzen duelarik.
Kontzeptua korronte alternorako neurketetara James Clerk Maxwellek hadatu zuen 1865ean eta gero Alan Blumleinek hobetua 1926. urtea inguru.
Jatorrizko zubiaren eraldaketak[aldatu | aldatu iturburu kodea]
Wheatstone zubia oinarrizko zubia da, baina badaude erresistentzia mota ezberdinak neurtzeko eraldaketak, zeinetarako oinarrizko wheatstone zubia ez da egokia. Eraldaketa batzuk hauek dira:
- Carey Foster zubia, erresistentzia txikiak neurtzeko
- Kelvin Varley Slide
- Kelvin zubi bikoitza
- Maxwell zubia























