Kirchhoffen zirkuituen legeak
Kirchhoffen legeak zirkuitu elektrikoetan karga eta energiaren kontserbazioarekin tratatzen duten bi berdinketa dira. Hauek leheneko aldiz 1845ean Gustav Kirchhoffek deskribatu zituen. Ingeniaritza elektrikoan oso erabilera zabala dute.
Zirkuituen bi legeak zuzenean Maxwellen ekuazioetatik lortu daitezke, baina Kirchhoffek Maxwell baino lehenago aurkitu zituen eta gero Georg Ohmek zabaldu zituen.
Korrontearen legea[aldatu | aldatu iturburu kodea]


Kirchhoffen korrontearen legea, (KCL - Kirchhoff's Current Law ingelesez), Kirchhoffen nodoen legea edo Kirchhoffen lehenengo legearen izenarekin ere ezagutzen da.
- Karga elektrikoaren kontserbazio printzipioak zera inplikatzen du:
Zirkuitu elektriko bateko edozein nodotan (elkarketa puntua) sartzen diren korronteen baturak eta irteten diren korronteen baturak balio berdina ematen dute.
Nodora sartzen diren korronteak positiboak eta nodotik ateratzen direnak negatiboak izatearen konbentzioa hartzen badugu (edo kontrakoa), printzipio hau honela adierazi daiteke:
Non n nodora sartu edo bertatik ateratzen diren adar guztien kopurua den.
Formula hau ere korronte konplexuentzat baliagarria da:
Lege hau kargaren kontserbazioan oinarritzen da, non karga (coulombetan neurtuta) korrontea (amperetan) eta denboraren (segundotan neurtuta) arteko biderkadura den.
Karga dentsitatea aldatzen[aldatu | aldatu iturburu kodea]
Fisikoki, kondentsadorearen gainazalekin murrizpenak Kirchhoffen korrontearen legea bakarrik aplikatzen den puntuan karga dentsitatea konstante denean baliagarria dela esan nahi du. Normalean hau ez da arazo bat indar elektrostatikoak direla eta: kargen handitzeak kargak bananduko lituzketen banantzen indarrak sortuko lituzke.
Hala eta guztiz ere, kargen handitzea kondentsadore batean gerta daiteke, zeinetan karga normalean bi gainazal paraleloetan hedatzen den eta bi hauen artean bi gainazaletako karga positibo eta negatiboen bilketa elkartu eta deuseztatzea eragozten duen hutsune fisiko bat dago. Kasu honetan, kondentsadorean sartzen den korronte elektrikoaren fluxua ez da zero, baina kargaren bilketaren ratioaren berdina da. Hala ere, dD/dt korrontearen desplazamendu hau kontutan hartzen bada, Kirchhoffen korrontearen legea berriz betetzen da. (Hau bakarrik beharrezkoa da baldin eta korrontearen legea kondentsadore baten gainazal batean aplikatu nahi badugu. Zirkuituen analisian, normalean, kondentsadore bat unitate bat bezala hartzen da, eta kasu honetan jatorrizko korrontearen legea betetzen da, kondentsadore baten alde batetik sartzen den korrontea eta bestetik ateratzen dena berdinak baitira.)
Modu teknikoago batean adierazita, Kirchhoffen korrontearen legea Ampereren legearen dibergentzia Maxwellen zuzenketarekin hartuta eta Gaussen legearekin konbinatuz lor daiteke, hurrengoa lortuz:
Hau kargaren kontserbazioaren ekuazioa besterik ez da (forma integralean zera dio, itxitako gainazal batean zehar ateratzen den korrontea eta bolumenaren barrualdeko kargaren galera ratioa berdinak direla (Dibergentziaren teorema)). Kirchhoffen korrontearen legea korrontearen dibergentzia zero izatea baieztapenarekiko baliokidea da, eta hau denborarekiko ρ aldaezinarentzat egia da, eta egia da beti baldin eta korrontearen desplazamendua Jn sartzen bada.
Erabilerak[aldatu | aldatu iturburu kodea]
Kirchhoffen korrontearen legeko bertsio matriziala, SPICE bezalako, zirkuitu simulatzaile programa gehienen oinarria da.
Tentsioaren legeak[aldatu | aldatu iturburu kodea]
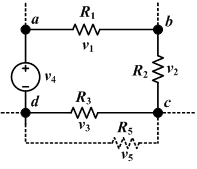
Kirchhoffen tentsioaren legeari (KVL - Kirchhoff's Voltage Law ingelesez), Kirchhoffen bigarren legearen izena ere ematen zaio.
Edozein saretan ematen den tentsio-erorketen baturak eta sorgailuen tentsioen baturak balio berdina eman behar duela.
- Edozein sare elektrikoetan, potentzial diferentzien baturak 0 (zero) izan behar du.
Hemen,n neurtutako tentsio guztien kopurua da. Tentsioak konplexuak ere izan daitezke:
Lege hau eremu potentzial batek emandako eta hartutako energiaren kontserbazioa oinarritzen da (disipazioa dela eta energia kontutan hartu gabe). Tentsio potentzial bat emanda, itxitako bide bat osatzen duen karga batek ez du energia galtzen ezta irabazten ere bere jatorrizko potentzial mailara iristen dean.
Lege hau betetzen da nahiz eta zirkuituan erresistentzia (energiaren disipazioa eragiten duena) agertu. Kasu honetan legearen baliagarritasuna uler daiteke, energia disipazioa dela eta, karga bere hasierako puntura itzultzen ez dela ohartuz gero. Karga batek terminal negatiboan bukatuko du positiboan ordez. Honek esan nahi du potentzial diferentziak emandako energia guztia erresistentziak kontsumitu duela eta honek energia galtzen duela beroa disipatuz.
Laburbilduz, Kirchhoffen tentsioaren legeak ez du osagai elektrikoen (erresistentzia, kondentsadore, etab) energiaren irabazi edo galerekin. Tentsio iturriak sortzen duten eremu potentzialaz arduratzen da legea. Eremu potentzial honetan, berdin dio ze osagai elektriko dauden, eremu potentzialak emandako energiaren irabazia zero izan behar da karga batek begizta itxi bat osatzen duenean.
Eremu eta potentzial elektrikoak[aldatu | aldatu iturburu kodea]
Kirchhoffen tentsioaren legea goian esan bezala hurrengo baieztapenaren baliokidea da: balio bakarreko potentzial elektrikoa zirkuituko puntu bakoitzari esleitu ahal zaio (eremu bektorial kontserbatibo bat potentzial eskalar baten gradientea bezala adieraz daitekeen bezala). Orduan zirkuituko edozein begizta itxiko irudizko ibilbidea egingo balu bezala gertatzen diren potentzial honetako aldaketen batuketa zero izan beharko luke.
Hau energiaren kontserbazio printzipioaren ondorio bezala ikus daiteke. Beste aldetik, posible izango zen zirkuituan zehar korrontea zirkulu batean pasatzen duen etengabeko mugimenduko makina bat eraikitzea.
Potentzial elektrikoa eremu elektriko baten gaineko integrala bezala definituta dagoela kontutan hartuz, Kirchhoffen tentsioaren legea hurrengo modu baliokidean adieraz daiteke:
eremu elektrikoaren integrala, C begizta itxitik zehar, zero dela baieztatzen du.
Forma bereziagora itzultzeko, integral hau zatitu daiteke osagai zehatzetako tentsioa lortzeko.
Hau Faraday-ren indukzio legearen sinplifikazio bat da, begizta itxia elkartuko zuen eremu magnetiko aldakorrik ez dagoeneko kasu berezirako. Beraz, praktikoki nahikoa da erresistentziak eta kondentsadoreak bakarrik dituzten zirkuituak azaltzeko.
Eremu magnetiko baten aurrean eremu elektrikoa ez da kontserbakorra eta beraz ezin du definitu potentziala eskalar hutsa bezala-zirkuituaren inguruko eremu elektrikoaren integrala ez da zero. Hau energia eremu magnetikotik korrontera (edo kontrakoa) transferitzen ari delako da. Induktoreak dituzten zirkuituetan Kirchhoffen tentsioaren legea "konpontzeko", zirkuituko induktantzia bakoitzarekin potentzial erorketa efektibo bat, edo indar elektroeragile bat elkartzen dira, hauen balioa eremu elektrikoaren integralaren zerotik aldentzen den balioa delarik Faradayren indukzioaren legeari jarraituz.
Erreferentziak[aldatu | aldatu iturburu kodea]
Ingelesezko bertsioko erreferentziak
Ikus, gainera[aldatu | aldatu iturburu kodea]
- Faraday-ren indukzio legea
- Gaussen legea
- Maxwellen ekuazioak
- Energiaren kontserbazioa
- Sareen korronteen analisia
- SPICE (Zirkuituak simulatzeko programa)







