Viviani-ren teorema

ℓ + m + n = h (h: garaiera)

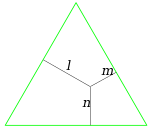
Vivianiren teoremak —Vincenzo Vivianiren omenez horrela izendatua— hau dio:

Triangelu aldeberdinaren barneko edozein puntutik triangeluaren aldeetarainoko distantzien batura eta triangeluaren garaiera berdinak dira.

Teorema hau poligono aldeberdinetarako eta poligono angeluberdinetarako ere heda daiteke: Poligono aldeberdinaren edo angeluberdinaren barneko edozein puntutik poligonoaren aldeetarainoko distantzien batura konstantea da.

Froga

Teorema oso erraz froga daiteke triangeluen azalerak alderatuz. Eman dezagun ABC triangelu aldeberdin bat, non h garaiera den eta aldeetako luzera a. Triangeluaren barneko edozein puntu P bada, eta ℓ, m, n distantziak P puntutik aldetarainokoak, ABC triangeluaren azalera hau da:

$Azalera(ABC)=Azalera(ABP)+Azalera(ACP)+Azalera(BCP)$

${\frac {a\cdot h}{2}}={\frac {a\cdot \ell }{2}}+{\frac {a\cdot m}{2}}+{\frac {a\cdot n}{2}}$

$h=\ell +m+n\,$

frogatu nahi genuen bezala.

Aplikazioak

Metanoaren sukoitasun-diagrama

Vivianiren teoremari esker, triangelu aldeberdinaren aldeekiko zuzen paraleloak koordenatu gisa erabil daitezke diagrama hirutarretarako; adibidez, sukoitasun-diagrametarako. Orokorrean, era berean, hala eraikitako koordenatuak simplex erregular batean ere erabil daitezke.

Kanpo estekak

• (Ingelesez) Weisstein, Eric W.: "Viviani's Theorem" MathWorld-en.
• (Ingelesez) Viviani's Theorem: What is it?, Cut the knot
• (Ingelesez) Viviani's Theorem, Jay Warendorff (Wolfram Demonstrations Project)

• Datuak: Q852183
• Multimedia: Viviani's theorem / Q852183