Simetria-talde
- Ez nahasi talde simetrikoarekin.
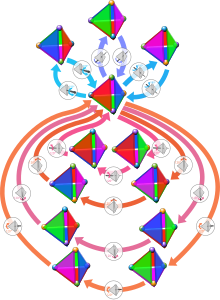
Simetria-taldea eragiketen edo transformazio geometrikoen talde bat da, ezaugarri geometriko edo fisiko jakin bat aldatzen ez duten transformazioen taldea, hain zuzen ere. Kontzeptua garrantzitsua da bai Geometrian bai Mekanika lagrangearrean, bai eta Eremu-teoria kuantikoan ere.
Simetria-taldea Geometrian[aldatu | aldatu iturburu kodea]
Geometrian, planoko puntuen multzo bat transformazio batekiko aldaezina dela esaten da, transformazio horren bidez multzo berbera lortzen denean. Esate baterako, triangelu aldeberdin bat 120°, 240° edo 360° biratuz, triangelu berbera lortzen da.
Puntuak hasierako posizio berberean uzten dituen transformaziori identitate-transformazio deritzo. Aurreko adibidean, 360°-ko bira da.
Hortaz, simetria-taldea da irudi lau bat aldatzen ez duten planoko transformazioen multzoa, eta gutxienez identitate-transformazioa hartzen du barnean. Adibidez, triangelu isoszelearen kasuan, bi baino ez dira triangelua aldatu gabe uzten duten transformazioak: Id identitate-transformazioa eta oinarriaren garaiarekiko s simetria. Beraz, triangelu isoszelearen simetria-taldea {Id,s} da.
Simetria-taldea beste arlotan[aldatu | aldatu iturburu kodea]

Mekanika kuantikoan eta Eremu-teoria kuantikoan, simetria-taldeak Lorentz-en transformazioen edo gauge transformazioen multzo bat da, sistema fisiko baten eboluzioa definitzen duen lagrangearra aldatu gabe uzten dutenena, hain zuzen ere.
Kristalografian, simetria-taldeak erabiltzen dituzte kristal batek dituen simetriak aztertzeko.
Ikus, gainera[aldatu | aldatu iturburu kodea]
Kanpo estekak[aldatu | aldatu iturburu kodea]
- (Ingelesez) Weisstein, Eric W.: "Symmetry Group" MathWorld-en.
- (Ingelesez) Weisstein, Eric W.: "Tetrahedral Group" MathWorld-en.
