Zirkunferentzia zirkunskribatu

Poligono zikliko (P) baten zirkunferentzia zirkunskribatua (C) eta zirkunzentroa (O).

Geometrian, poligono baten zirkunferentzia zirkunskribatua zirkunferentzia bat da, poligonoaren erpin guztiak ukituz inguratzen duena. Zirkunferentzia horren zentroa zirkunzentro deitzen da eta erradioa zirkunerradio.

Poligono inskribatuari poligono zikliko esaten zaio (batzuetan poligono ziklokide, erpinak ziklokideak direlako). Poligono sinple erregular guztiak, hiruki guztiak eta laukizuzen guztiak ziklikoak dira. Poligono ziklikoetan, zirkunzentroa poligonoaren aldeen erdibitzaileen ebaki-puntua da.

Hirukiak

Hirukietan, hiru aldeen erdibitzaileek puntu batean ebakitzen dute elkar; zirkunzentroan, hain zuzen ere. Zirkunzentroa hiru erpinetatik distantzia berera dago.

Hirukiaren erpinak, aldeen muturrak direnez gero, haien erdibitzaileen puntuetatik distantzia berera daude; beraz, horien ebaki-puntua hiru erpinetatik distantziakidea da: zirkunzentroa (zirkunferentzia zirkunskribatuaren zentroa).

Zirkunzentroaren kokagunea hirukiaren araberakoa da:

• 

  Triangelu zorrotzetan (angelu guztiak zorrotzak dira), zirkunzentroa hirukiaren barnealdean dago.

• 

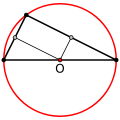
  Triangelu zuzenetan (angelu bat zuzena da), zirkunzentroa hipotenusaren erdigunean dago. Hori zirkuluaren Talesen teoremaren berezitasun bat da.

• 

  Triangelu kamutsetan (angelu bat kamutsa da), zirkunzentroa hirukiaren kanpoaldean dago.

Lauki ziklikoak

Lauki zikliko batzuk.

Artikulu nagusia: Lauki zikliko

Zirkunskribagarriak diren laukiek, lauki ziklikoek, propietate bereziak dituzte; esate baterako, aurkako angeluak betegarriak dira (haien batura 180° da, edo π radian).

Ikus, gainera

• Zirkunferentzia inskribatua
• Intzentroa
• Eszentroa
• Eulerren zuzena
• Simsonen zuzena
• Arku kapaza

Kanpo loturak

• (Ingelesez) Triángulo inscripto Webgune elkarreragilea
• (Ingelesez) Hirukiaren zirkunzentroa Webgune elkarreragilea

MathWorld

• (Ingelesez) Weisstein, Eric W., "Circumcircle" MathWorld-en.
• (Ingelesez) Weisstein, Eric W., "Cyclic Polygon" MathWorld-en.
• (Ingelesez) Weisstein, Eric W., "Steiner circumellipse" MathWorld-en.