Poligono erregular

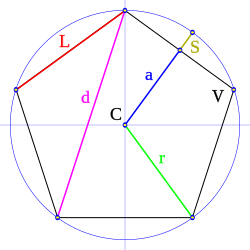
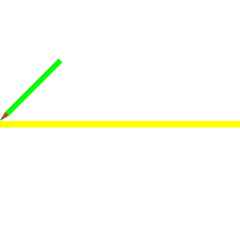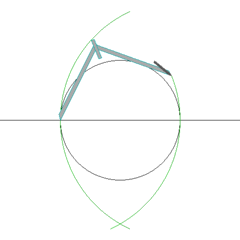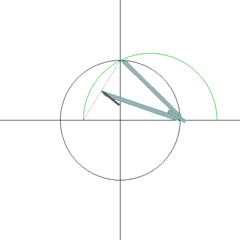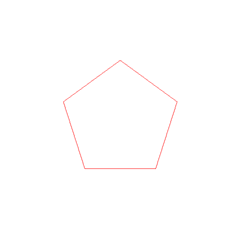
Zirkunferentzia batean inskribatutako pentagono erregularra:

• C = zirkunferentzia zirkunskribatuaren zentroa
• V = poligonoaren erpin bat
• L = poligonoaren alde bat
• d = poligonoaren diagonal bat
• r = zirkunferentzia zirkunskribatuaren erradioa
• a = poligonoaren apotema

Geometrian, poligono bat erregularra da, aldeberdina (alde guztiak luzera berekoak dira) eta angeluberdina (angelu guztiak neurri berekoak dira) bada.

Poligono erregularrak bi motatakoak izan daitezke: ganbilak eta ahurrak (izar itxurakoak azken horiek, izar-poligono izenekoak).

Hiru eta lau aldeko poligono erregularrak triangelu aldeberdina eta karratua dira, hurrenez hurren; alde gehiagoko poligono erregularrak izendatzeko, erregular terminoa gehitzen da (pentagono erregularra, hexagono erregularra...).

Poligono erregularren elementuak

• Aldea (L): poligonoa osatzen duten zuzenkietako bakoitza
• Erpina (V): poligono baten bi aldek elkar ebakitzen duten puntua
• Zentroa (C): erpinetatik distantziakidea den puntua
• Erradioa (r): poligonoaren zentroa eta erpin bat lotzen dituen zuzenkia
• Apotema (a): aldearekiko elkarzuta den eta poligonoaren zentroraino doan zuzenkia
• Diagonala (d): ondoz ondokoak ez diren bi erpin lotzen dituen zuzenkia
• Perimetroa (P): alde guztien luzeren batura

Poligono erregularren propietateak

• n aldeko poligono erregularrak n ordenako biraketa-simetria du.

• Erpin guztiak zirkunferentzia berean daude (zirkunferentzia zirkunskribatua); hau da, erpinak ziklokideak dira. Beraz, poligono erregularrak ziklikoak dira.

• Aurreko bi propietateetatik, eta kontuan hartuta aldeak berdinak direla, ondoriozta daiteke poligono erregular guztiek zirkunferentzia inskribatu bat daukatela, alde guztien erdiguneak barnetik ukitzen dituena. Hortaz, poligono erregularrak poligono ukitzaileak dira.

• Poligono erregularretan, angelu zentralak eta kanpo-angeluak berdinak dira.

Poligono erregularren angeluak

  α = angelu zentrala,
  β = barne-angelua,
  γ = kanpo-angelua

Angelu zentrala

• Poligono erregular baten angelu zentralak ($\alpha \,$) kongruenteak dira, eta haien neurria honela kalkula daiteke, poligonoaren alde kopuruaren (n) arabera:

$\alpha ={\frac {360^{\circ }}{n}}\;$ (gradu hirurogeitarretan)

$\alpha ={\frac {2\pi }{n}}\;$ (radianetan)

Barne-angelua

• Poligono erregular baten barne-angelua ($\beta \,$) honela kalkula daiteke:

$\beta =180^{\circ }\cdot {\frac {(n-2)}{n}}\;$ (gradu hirurogeitarretan)

$\beta =\pi \cdot {\frac {(n-2)}{n}}\;$ (radianetan)

• Poligono erregular baten barne-angeluen batura ($\sum \beta \;$), beraz:

$\sum \beta =180^{\circ }\cdot {(n-2)}\;$ (gradu hirurogeitarretan)

$\sum \beta =\pi \cdot {(n-2)}\;$ (radianetan)

Kanpo-angelua

• Poligono erregular baten kanpo-angelua ($\gamma \;$) honela kalkula daiteke:

$\gamma ={\frac {360^{\circ }}{n}}\;$ (gradu hirurogeitarretan)

$\gamma ={\frac {2\pi }{n}}\;$ (radianetan)

• Poligono erregular baten kanpo-angeluen batura ($\sum \gamma \,$), beraz:

$\sum \gamma =360^{\circ }\;$ (gradu hirurogeitarretan)

$\sum \gamma =2\pi \;$ (radianetan)

Poligono erregular batzuk

• 
  Triangelu aldeberdina (triangelu erregularra) (3)
• 
  Karratua (lauki erregularra) (4)
• 
  Pentagono erregularra (5)
• 
  Hexagono erregularra (6)
• 
  Heptagono erregularra (7)
• 
  Oktogono erregularra (8)
• 
  Eneagono erregularra (9)
• 
  Dekagono erregularra (10)
• 
  Endekagono erregularra (11)
• 
  Dodekagono erregularra (12)
• 
  Tridekagono erregularra (13)
• 
  Tetradekagono erregularra (14)

Oharra: Poligono erregularrak zenbat eta alde gehiago izan, orduan eta zirkunferentzia baten antz handiagoa izango du.

Poligono erregularraren azalera

Poligono erregular baten azalera kalkulatzeko, ezagunak ditugun elementuen arabera, hainbat formula daude:

Azalera: perimetroaren eta apotemaren arabera

$A={\frac {P\cdot a}{2}}$

Froga

Poligonoaren aldea L triangeluaren oinarria da, eta a apotema triangeluaren garaiera; beraz, triangeluaren azalera, $A_{h}$, hau da: $A_{h}={\frac {L\cdot a}{2}}\;$ n aldeko poligonoak n triangelu ditu, eta guztizko azalera hau da: $A={\frac {L\cdot a}{2}}\cdot n={\frac {L\cdot n\cdot a}{2}}\;$ L aldearen luzera bider n (alde kopurua) perimetroa denez gero, formula hau dugu: $A={\frac {P\cdot a}{2}}\;$

Azalera: alde kopuruaren eta apotemaren arabera

$A=a^{2}\cdot n\cdot \tan \left({\frac {\pi }{n}}\right)\$

Froga

Hau jakinda: $A={\frac {L\cdot n\cdot a}{2}}\$ eta $\delta ={\frac {\pi }{n}}\$ kontuan hartuta, angelu zentralaren erdia baita (radianetan). trigonometriako formulak erabiliz, hau ondoriozta daiteke: $L=2\cdot a\cdot \tan \left({\frac {\pi }{n}}\right)$ Aldea azalerarako formulan ordezkatuta: $A={\frac {(2\cdot a\cdot \tan \left({\frac {\pi }{n}}\right))\cdot n\cdot a}{2}}\$ Azkenik: $A=a^{2}\cdot n\cdot \tan \left({\frac {\pi }{n}}\right)\$

Azalera: alde kopuruaren eta erradioaren arabera

$A={\frac {nr^{2}\sin({\frac {2\pi }{n}})}{2}}\;$

Froga

Trigonometriako formulak erabiliz, hau ondoriozta daiteke: $L=2r\sin({\delta })\;$ $a=r\cos({\delta })\;$ non angelu zentrala hau den: $\alpha =2\delta ={\frac {2\pi }{n}}\;$ Poligonoaren azalera hau denez: $A={\frac {L\cdot n\cdot a}{2}}\;$ eta lehen kalkulatutako aldea eta apotemaren balioak ordezkatuz, hau dugu: $A={\frac {2r\sin({\delta })\cdot n\cdot r\cos({\delta })}{2}}\;$ Ordenatuta: $A={\frac {nr^{2}\cdot 2\sin({\delta })\cos({\delta })}{2}}\;$ Trigonometrian, ezaguna da berdintza hau: $2\sin({\delta })\cos({\delta })=\sin({2\delta })\;$ Emaitza hau da: $A={\frac {nr^{2}\sin({\alpha })}{2}}\;$ Edo beste era honetan: $A={\frac {nr^{2}\sin({\frac {2\pi }{n}})}{2}}\;$

Azalera: aldearen arabera

$A=n\cdot {\cfrac {L^{2}}{4}}\cdot \tan \left({\cfrac {\pi }{2}}{\cfrac {(n-2)}{n}}\right)$

Froga

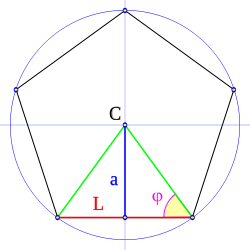
Poligonoaren azalera hau denez: $A=n\cdot {\frac {L\cdot a}{2}}\;$ Erabil dezagun $\varphi$ sinboloa "L" aldearen eta "r" erradioaren arteko angelua izendatzeko: $\varphi ={\frac {\pi -\alpha }{2}}\ ={\frac {\pi -{\frac {2\pi }{n}}}{2}}\ ={\frac {\pi }{2}}{\frac {(n-2)}{n}}\;$ Definizioz, tangentearen balioa hau da (apotemaren eta aldearen arabera): $\tan \varphi ={\frac {a}{\frac {L}{2}}}={\frac {2a}{L}}$ Apotema askatuz gero, hau dugu: $a={\frac {L\cdot \tan \varphi }{2}}$ Adierazpen hori azaleraren formulara eramanda: $\left.{\begin{array}{l}A=n\cdot {\cfrac {L\cdot a}{2}}\\\\a={\cfrac {L\cdot \tan \varphi }{2}}\\\\\varphi ={\cfrac {\pi }{2}}{\cfrac {(n-2)}{n}}\end{array}}\right\}\quad \longrightarrow \quad A=n\cdot {\cfrac {L^{2}}{4}}\cdot \tan \left({\cfrac {\pi }{2}}{\cfrac {(n-2)}{n}}\right)$

Laburpen-taula

Pentagono erregular bat eraikitzen

Oharra: alde kopuru oso handia duen poligonoaren kasuan, barne-angeluek lauak izatera joko dute, aldea nulua izatera eta azalera π zenbakiaren baliorantz.

Alde, angelu eta erpin kopurua	Poligonoa	Irudia	Barne-angelua	Aldea	Azalera	Animazioa: eraikitze grafikoa erregela eta konpasa erabiliz
3	Triangelu aldeberdina		60°	√3≅1,732	3/4·√3≅1,299	Eraikitze zehatza
4	Karratua		90°	√2≅1,414	2	Eraikitze zehatza
5	Pentagonoa		108°	≅1,176	≅2,378	Eraikitze zehatza
6	Hexagonoa		120°	1	3/2·√3≅2598	Eraikitze zehatza
7	Heptagonoa		≅128,57°	≅0,868	≅2,736	Gutxi gorabeherako eraikitzea
8	Oktogonoa		135°	≅0,765	2·√2≅2,828	Eraikitze zehatza
9	Eneagonoa		140°	≅0,684	≅2,893	Gutxi gorabeherako eraikitzea
10	Dekagonoa		144°	≅0,618	≅2,939	Eraikitze zehatza
11	Endekagonoa		≅147,27°	≅0,563	≅2,974	Gutxi gorabeherako eraikitzea
12	Dodekagonoa		150°	≅0,518	3	Eraikitze zehatza
13	Tridekagonoa		≅152,31°	≅0,479	≅3,021	Gutxi gorabeherako eraikitzea
14	Tetradekagonoa		≅154,29°	≅0,445	≅3,037	Gutxi gorabeherako eraikitzea
15	Pentadekagonoa		156°	≅0,416	≅3,051	Eraikitze zehatza
16	Hexadekagonoa		157,5°	≅0,390	≅3,061	Eraikitze zehatza
17	Heptadekagonoa		≅158,82°	≅0,367	≅3,071	Eraikitze zehatza 34-gonoa, 51-gonoa 85-gonoa, 255-gonoa
18	Oktodekagonoa		160°	≅0,347	≅3,078	Gutxi gorabeherako eraikitzea
19	Eneadekagonoa		≅161,05°	≅0,329	≅3,085	Gutxi gorabeherako eraikitzea
20	Ikosagonoa		162°	≅0,313	≅3,090	Eraikitze zehatza
257	257-gonoa		≅178,6°	≅0,024	≅3,141	Eraikitze zehatza
65.537	65.537-gonoa		≅179,9945°	≅0,000096	≅3,1416	Eraikitze partziala

Kanpo estekak

• Datuak: Q714886
• Multimedia: Regular polygons / Q714886