Gainezarmen printzipioa
Gainezarmen printzipioa matematikako tresna bat da, problema lineal bat bi zatitan banatzeko edo bi azpiproblema errazetan deskonposatzeko. Horrela, jatorrizko problema hau beste azpiproblemen batuketa edo gainezarmenaren bidez da.
Adibideak[aldatu | aldatu iturburu kodea]
Hooken legea[aldatu | aldatu iturburu kodea]
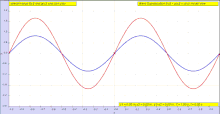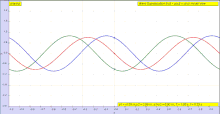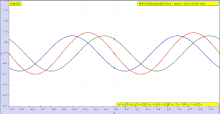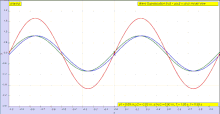
Periodo elastiko batean, deformazioak eragiten dituzten tentsioarekiko proportzionalak dira.
Y (deformazioak) = K·X (tentsioak)
Kausa tentsioak dira eta efektua deformazioak. Kasu honetan, X eta Y-ren arteko erlazioa lineala da, beraz, Gainezarmen Printzipioa erabili dezakegu. Honek tentsiopean dagoen gorputz baten problema hainbat azpiproblematan banatu dezakegula esan nahi du. Azpiproblema bakoitzean indar gutxi hartzen dira kontutan, beraz deformazio bakoitza kalkula daiteke, eta guztien batura deformazio totala izango litzateke.
Elektronika[aldatu | aldatu iturburu kodea]

Hau da, nodo batetik irteten den korrontearen intentsitatea nodo horretara heldu den intentsitate desberdinen batura da.
