Pertzeptroi

Ikasketa automatikoan, pertzeptroia (McCulloch-Pitts neurona) sailkapen bitarra egiteko ikasketa gainbegiratutako algoritmo bat da. Sailkapen bitarra funtzio bat da, zenbakien bektore batek irudikatzen duen sarrera bat mota zehatz batekoa den ala ez erabaki dezakeena. Sailkatzaile lineal mota bat da, hau da, sailkapen-algoritmo bat, bere iragarpenak funtzio lineal batean oinarrituz egiten dituena, pisu-bektore eta ezaugarri-bektore bat konbinatuz.

Definizioa

Pertzeptroia neurona bateko eredu matematiko sinpleena da. Sailkatzaile bitar bat da, eta datuak bi taldetan banatzen dituen ikasketa gainbegiraturiko sistema bat da. Atalase-funtzioa izeneko sailkatzaile bitar bat ikasteko algoritmo bat da: sarrera (balio errealeko bektore bat) $f(x)$ irteera-balioan (balio bitar bat) mapatzen duen funtzioa:

$f(x)=\theta (wx+b)$

non $\theta$ aktibazio funtzioa, $w$ pisu errealen bektorea, $b$ alborapena eta $w\cdot x$ biderkadura eskalarra den $\sum _{i=1}^{m}w_{i}x_{i}$. Batukariaren m zenbakia, pertzeptroiaren sarrera kopurua da. Alborapenak jatorritik erabaki-muga desplazatzen du, eta ez dago inolako sarrera-balioaren mende.

Era berean, $w\cdot x+b=(w,b)\cdot (x,1)$ ekuaziotik abiatuta, $b$ alborapen-terminoa beste pisu gisa gehitu dezakegu $w_{m+1}$ eta 1 koordenatua gehitu sarrera bakoitzari. Ondoren, jatorritik pasatzen den sailkatzaile lineal gisa idatz dezakegu:

$f(x)=\theta (w\cdot x)$

$f(x)$-ren balio bitarra (0 edo 1) sarrerako $x$ bektoreko instantzia positibo edo negatibo moduan sailkatzeko erabiltzen da. Espazioari dagokionez, alborapenak erabaki mugaren posizio aldatzen du baina ez honen orientazioa.

Geruza bakarreko pertzeptroi izenarekin ere ezaguna da, geruza anitzeko pertzeptroitik desberdintzeko. Sailkatzaile lineala denez, geruza bakarreko pertzeptroia aurreranzko neurona-sare sinpleena da.

Ikaskuntza

Pertzeptroian bi ikaskuntza mota daude: lehenengoak ikasketa-tasa bat erabiltzen du eta bigarrenak ez. Ikasketa-tasa horrek arindu egiten du pisuen balioen aldaketa.

Aldagaien definizioa

Ikasketa-algoritmoa berdina da neurona guztientzat, eta jarraian datorren guztia neurona bakar bati aplikatzen zaio isolamenduan. Lehenengo aldagai batzuk definitzen dira:

• $x(j)$ j. posizioan dagoen sarrerako bektoreari egiten dio erreferentzia
• $w(j)$ j. posizioan dagoen pisu-bektoreari egiten dio erreferentzia
• $y$ neurona sarearen irteera
• $\delta$ espero den irteera
• $\alpha$ konstante bat da non $0<\alpha <1$

Ikaskuntza algoritmoa

Bi ikaskuntza moten desberdintasuna urrats honetan dago. Lehenengo ikaskuntza motarako, ikaskuntza-tasa erabiliz, pisuak horrela eguneratuko ditugu:

• $w(j)'=w(j)+\alpha (\delta -y)x(j)$

Bigarren ikaskuntza motarako, ikaskuntza-tasa erabili gabe, pisuak horrela eguneratuko ditugu:

• $w(j)'=w(j)+(\delta -y)x(j)$

Beraz, iterazio bakoitzaren ondoren pisu-bektorea eguneratu egingo da $y$ irteera $\delta$ iragarpenarekin bat dator ez denean. Horrela, pausoka iragarpena fintzen joango da. Hainbat iterazio egiteko, aldagai gehiago definitu behar ditugu:

• $x_{i}$ $i$. iterazioaren sarrera-bektoreari egiten dio erreferentzia
• $w_{i}$ $i$.iterazioaren pisu-bektoreari egiten dio erreferentzia
• $y_{i}$ $i$.iterazioaren irteera balioari egiten dio erreferentzia
• $D_{m}=\{(x_{1},y_{1}),...,(x_{m},y_{m})\}$ m iterazioko ikaskuntza prozesuari egiten dio erreferentzia

Iterazio bakoitzean, honela eguneratzen da pisu-bektorea:

• $(x,y)$ sarrera-irteera pare bakoitzeko, $D_{m}=\{(x_{1},y_{1}),...,(x_{m},y_{m})\}$
• $(x_{i},y_{i},w_{i})$ hirukotea, eguneratze funtziotik pasako dugu: $w(j)'=w(j)+\alpha (\delta -y)x(j)$

Ikaskuntza prozesuan $D_{m}$ linealki bereizgarria dela esaten da baldin eta $\gamma$ balio positibo bat eta $w$ pisu-bektore bat existitzen badira non $y_{i}\cdot (\langle -w,x_{i}\rangle +u)>\gamma$ betetzen duten $i$ guztientzako.

Novikoff-ek (1962) frogatu zuen ikaskuntza-algoritmoak iterazio kopuru mugatu baten ondoren konbergitzen duela, baldin eta datuak linealki bereizgarriak badira eta errore kopurua honetara mugatuta badaude: $({\frac {2R}{\gamma }})^{2}$

Hala ere, datuak linealki bereizgarriak ez badira, aurreko algoritmo-lerroak ez du bermatzen konbergituko duenik.

Konbergentzia

Pertzeptroi bakarra sailkatzaile lineal bat da. Sarrera-bektore guztiak ongi sailkatuta dauden kasuan bakarrik irits daiteke egoera egonkor batera. $D$ entrenamendu datu multzoa ez bada linealki banagarria, hau da, kasu positiboak ezin badira kasu negatiboetatik banandu hiperplano baten bidez, orduan algoritmoak ez du konbergituko ez delako soluziorik existituko.

Banangarritasun linerrak denbora ordena honetan frogagarria da $min(O(n^{d/2}),O(d^{2n}),O(n^{d-1}\ln {n}))$ , non $n$ datu puntu kopurua den , eta $d$ puntu bakoitzaren dimentsio kopurua den.

Entrenamendu datu multzoa linealki banangarria bada, bermatuta dago pertzeptroiaren algoritmoak konbergituko duela errore kopuru finitu baten ondoren. Rosenblatt eta bestek (1989) emandako teorema:

Pertzeptroiaren konbergentziaren teorema: $D$ datu multzoa edukita, $max_{(x,y)\in D}||x||_{2}=R$ betetzen bada, linealki banangarria da $w^{*}$ unitate bektorearen bidez, $\gamma$ edukita: $\gamma :=min_{(x,y)\in D}y(w^{*}\cdot x)$ izanda. Asko bezala $(R/\gamma )^{2}$ akatsetara iristean, algoritmoa konbergitu egingo da edozein ikasketa tasarentzat, eta edozein datu multzorentzat.

Hurrengo froga (Novikoff 1962) sendoagoa da. Frogaren ideia hau da: pisu-bektorea mugatutako balio baten araberakoa izango da berarekin biderketa eskalar negatibo bat duen norabide batean. Horregatik $O({\sqrt {t}})$-ren gainetik mugatuta egon daiteke, non $t$ pisu bektorearen aldaketa kopurua den. Hala ere, $O(t)$-tik behera ere mugatuta egon daiteke, baliozko pisu-bektore ezezagun bat existitzen bada. Kasu horretan, aldaketa guztiek norabide ezezagun horretara mugituko dute emaitza, sarrera-bektorean oinarritutako balio positibo batean.

Froga Demagun $t$ pausuan, $w_{t}$ pisudun bektoreak akats bat egiten duela $(x,y)$ puntuan, eta eguneraketa hau egiten duela: $w_{t}=w_{t}+r(y-f_{w_{t}}(x))x$. $y=0$ bada, balioa simetrikoa da, eta beraz, ez dugu kontuan hartuko. Bestela, $y=1$ bada, orduan $f_{w_{t}}(x)=0$, $f_{w^{*}}(x)$, eta $w_{t+1}=w_{t}+rx$ Banaketa marjinak ditugu hau betezen dutena: $w^{*}\cdot x\geq \gamma$ Horregatik, $w^{*}\cdot w_{t+1}-w^{*}\cdot w_{t}=w^{*}\cdot rx>r\gamma$ Gainera, $||w_{t+1}||_{2}^{2}-||w_{t}||_{2}^{2}=||w_{t}+rx||_{2}^{2}-||w_{t}||_{2}^{2}=2r(w_{t}\cdot x)+r^{2}||x||_{2}^{2}$ eta pertzeptroiak akats bat egin duenez, $||w_{t+1}||_{2}^{2}-||w_{t}||_{2}^{2}\leq ||x||_{2}^{2}\leq r^{2}R^{2}$ $w_{0}=0$ edukita hasi garenez, $N$ akats egin ondoren, $||w||_{2}\leq {\sqrt {Nr^{2}R^{2}}}$ eta gainera, $||w||_{2}\geq w\cdot w^{*}\geq Nr\gamma$ Biak konbinatuz, $N\leq (R/\gamma )^{2}$daukagu.

Nahiz eta bermatuta dagoen pertzeptroairen algoritmoa emaitza batera konbergituko dela edozein entrenamendu multzo banangarrirako, honek edozein soluzio har dezake eta problema askok kalitate aldakorreko soluzio asko onartu ditzakete. Arazo hau konpontzeko, pertzeptroiaren bertsio bat sortu zen egonkortasun optimoa duena. Bertsio horri lineal euskarri bektoredun makina deritzo gaur egun (Krauth eta Mezard, 1987).

Adibidea

OR eta AND funtzioak linealki bereizgarriak direnez, pertzeptroi bat erabili dezakegu horiek ikasteko.

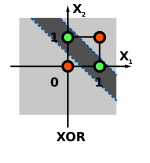
XOR funtzioa ezin da pertzeptroi bakar batekin ikasi klaseak bereizteko gutxienez bi lerro behar baitutu (0 eta 1). Geruza gehiagarri bat behar dugu pertzeptroi batekin ikaskuntza gauzatzeko.

Klase anitzeko pertzeptroia

Sailkatzaile linealen ikasketarako beste hainbat teknika bezala, pertzeptroia klase anitzeko sailkapenerako baliozkoa da. Kasu honetan, sarrera x eta irteera y, datu multzo arbitrario batetik hartuta daude.$f(x,y)$ ezaugarri errepresentazio bektoreak edozein sarrera-irteera pare mapatzen ditu dimentsio mugatuak dituen balio errealeko ezaugarri bektore batera. Aurreko kasuan bezala, ezaugarri bektorea w pisu bektorearekin biderkatzen da, baina orain, lortutako balioa hainbat irteera posibleen artean klase bat aukeratzeko erabiltzen da:

${\hat {y}}=argmax_{y}f(x,y)\cdot w$

Ikasketa adibideen gainean iteratzean datza aurreko kasuan bezala, bakoitzarentzat irteera bat iragarriz. Ideia nagusia da irteera eta benetako balioa berdinak ez direnean pisuen balioak aldatzea eta ezberdinak direnean pisuak eguneratzea. Eguneraketa honako hau izango litzake:

$w_{t+1}=w_{t}+f(x,y)-f(x,{\hat {y}})$

Klase anitzeko atzeraelikadura formulazio hau sailkapen bitarrerako pertzeptroiaren berdina izango da $x$ balio errealeko bektore bat denean, $y$-ren balioa $\{0,1\}$ multzokoa bada eta $f(x,y)=xy$ betetzen denean.

Problema zehatz batzuentzat, sarrera-irteeren errepresentazioak berariazkoak izan daitezke $argmax_{y}f(x,y)\cdot w$ efizienteki aurkitua izateko nahiz eta y multzo oso handi edo ia infinitu batetik lortu behar izan.

Kanpo estekak

• Neuronak programatzen: https://zientzia.eus/artikuluak/neuronak-programatzen/

• Datuak: Q690207