Jaiotza-heriotza prozesu
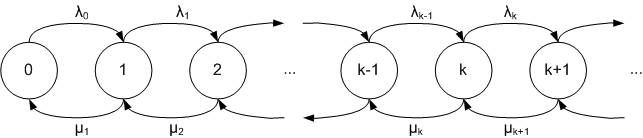
Jaiotza-heriotza prozesuak denbora jarraituko Markov kateen kasu berezi bat dira, non egoera trantsizioak bakarrik bi motakoak izan daitezkeen: jaiotzea, egoera aldagaiari bata gehitzen diona, eta heriotza, egoera batean gutxitzen duena. Ereduaren izena aplikazio arrunt batetik dator: populazioaren uneko tamaina adierazteko ereduetan erabiliak dira, non trantsizioak literalki jaiotzak eta heriotzak diren. Jaiotza-heriotza prozesuek aplikazio asko dituzte demografian, ilara-teorian, errendimendu ingeniaritzan, epidemiologian edo biologian. Adibidez, bakterioen eboluzioa, populazioko zenbat pertsonak duten gaixotasun bat edo supermerkatu bateko ilaran zenbat erosle egongo diren aztertzeko.
Jaiotze bat ematen denean prozesua egoeratik egoerara pasatzen da. Heriotza gertatzean berriz, prozesua egoeratik egoerara pasatzen da. Prozesua jaiotza tasa eta heriotza tasekin zehazten da.
Sarrera[aldatu | aldatu iturburu kodea]
Jaiotza-heriotza prozesu bat jaiotza prozesu purua da baldin eta guztietarako.
Jaiotza-heriotza prozesu bat heriotza prozesu purua izango da baldin eta guztietarako.
Poisson prozesu bat jaiotza prozesu purua izango da denean guztietarako.
M/M/1 eta M/M/C ereduak, biak ilara-teorian erabiliak, ilara infinitu bateko bezeroak deskribatzeko jaiotza-heriotza prozesuak dira.
denbora tarte txikian, hiru motako trantsizioak bakarrik dira posible: heriotza bat, jaiotza bat edo ez jaiotza ez heriotzarik. Jaiotza tasa (denbora unitatean) bada eta heriotza tasa , orduan trantsizio horien probabilitateak hauek dira, hurrenez hurren: , , eta .
Erabilera Ilara-teorian[aldatu | aldatu iturburu kodea]
Ilara-teorian jaiotza-heriotza prozesua da ilara ereduaren oinarrizko adibidea, M/M/C/K/∞/FIFO ilara Kendallen notazioan. Honek adierazten du ilararen etorrerak Poisson prozesuaren araberakoak direla, populazio infinitu batetik, bere zerbitzu denborek banaketa esponentziala jarraitzen duten C zerbitzari eta K toki daudela ilaran. Nahiz eta populazio infinitua izango dela onartu, eredu hau ona da telekomunikazio sistema hainbatentzat. Banaketa esponentzialean kopuruen arteko independentzia dagoenean, denborak infinituraino askeak izango dira trantsizioei buruz.
M/M/1 ilara[aldatu | aldatu iturburu kodea]

Zerbitzari bakarra egongo da tamaina infinituko bufferrarekin. Ausazkoa ez den ingurunean jaiotza-heriotza prozesuak ilara ereduan batezbeste epe luzekoak dira, beraz batezbesteko etorrera tasa moduan ematen da eta batezbesteko zerbitzu denbora bezala. Jaiotze-heriotza prozesu bat M/M/1 ilara da baldin eta,
Sistema t denboran k egoeran izateko probabilitatearen funtzio errekurtsiboa hau da:
M/M/C ilara[aldatu | aldatu iturburu kodea]

Zerbitzari anitzeko ilarak buffer infinitua du C zerbitzariekin. M/M/1 ilararekin alderatuz, desberdintza bakarra zerbitzu denbora da orain honelakoa izanik
eta
non
M/M/1/K ilara[aldatu | aldatu iturburu kodea]
Zerbitzari bakarra eta K tamainako bufferra (finitua) duen ilara da. Ilara mota hau telekomunikazioetan erabiltzen da, baita ere biologian populazioaren tamaina mugatuta dagoenean. Telekomunikazioetan berriro ere erabiltzen dira M/M/1 ilararen parametroak
Biologian, batez ere bakterioen hazkundearen analisian, populazioa zero denean ez dagoenez hazteko gaitasuna,
Gainera, K-k populazioaren limitea adierazten badu, non hortik aurrera bakterioen populazioaren soberakina hil egiten den
Probabilitatearen funtzio errekurtsiboa sistema k egoeran izateko t unean
Oreka[aldatu | aldatu iturburu kodea]
Ilara bat orekan dagoela esaten da baldin eta existitzen bada. Horretarako izan behar da.
M/M/1 ilara adibide moduan erabiliz, egoera egonkorraren ekuazioak hauek dira:
eta baldin badira guztietarako orduan ekuazioen kasu homogeneoan gaude eta honela laburtu daitezke:
Ikus, gainera[aldatu | aldatu iturburu kodea]
Bibliografia[aldatu | aldatu iturburu kodea]
- R. Jain. The Art Of Computer Systems Perfomance Analysis. 1. edizioa. 31. kapitulua: Analysis of a Single Queue; WILEY, 1991.
- G. Latouche, V. Ramaswami. Introduction to Matrix Analytic Methods in Stochastic Modelling, 1. edizioa. 1. kapitulua: Quasi-Birth-and-Death Processes; ASA SIAM, 1999.
- M. A. Nowak. Evolutionary Dynamics: Exploring the Equations of Life, Harvard University Press, 2006.
- K. S. Trivedi. Probability and Statistics with Reliability, Queuing and Computer Science Applications, 2. edizioa. 8. kapitulua: Continuous-Time Markov Chains; WILEY, 2002.
- J. Virtamo,"Birth-death processes"[1], 38.3143 Queueing Theory.








































