Superelipse

Superelipsea (edo Lamé-ren kurba) irudi geometriko bat da, koordenatu kartesiarretan honako ekuazio hau daukana:

$\left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1$

non n > 0 den, eta a eta b irudiaren ardatzen luzerak diren. Zenbatekoa den n, kasu hauek daude:

• n = 2 bada, ohiko elipse bat dugu (are gehiago: a = b bada, zirkunferentzia bat).
• n > 2 bada, hiperelipseak deitzen dira, erpinak kamutsak dituen laukizuzen itxurako irudiak. Muturreko kasuan, n infinitua (∞) balitz, ohiko laukizuzen bat genuke.
• n < 2 bada, hipoelipseak deitzen dira.

Adibide batzuk

• 
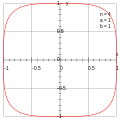
  Hiperelipsea (n = 4, a = b = 1)
• 
  Hipoelipsea (n = 3/2, a = b = 1)
• 
  Hipoelipsea (n = 1/2, a = b = 1)

Ekuazioa

Superelipsearen ekuazio parametrikoak hauek dira:

$\left.{\begin{aligned}x\left(\theta \right)&=\pm a\cos ^{\frac {2}{n}}\theta \\y\left(\theta \right)&=\pm b\sin ^{\frac {2}{n}}\theta \end{aligned}}\right\}\qquad 0\leq \theta <{\frac {\pi }{2}}$

Historia

Superelipsea aurkitzearen ospea Piet Hein daniar poeta eta zientzialariak hartu bazuen ere, berak ez zuen aurkitu superelipsea. Ostera, Gabriel Lamé frantziar matematikariak aurkitu zuen, elipsearen ekuazioa orokortzean.

Piet Heinek ezagutarazi egin zuen superelipsea, arkitekturan, hiri-diseinuan eta altzarigintzan; baita superarrautza aurkitu ere, superelipse honetatik abiatuta:

$\left|{\frac {x}{4}}\right|^{2.5}\!+\left|{\frac {y}{3}}\right|^{2.5}\!=1$

eta OX ardatzaren gainean birarazita.

Ikus, gainera

• Elipsea
• Elipsoidea
• Superelipsoidea
• Hiperbola
• Parabola
• Hipozikloidea
• Astroidea

Kanpo estekak

• Datuak: Q867058
• Multimedia: Superellipse / Q867058