Doppler efektua

Doppler efektua behatzailearen eta iturriaren arteko higidura erlatiboaren ondorioz gertatzen den itxurazko maiztasun-aldaketa da.
Efektu hau Christian Andreas Doppler fisikari austriarrak ikertu zuen. Doppler-ek bere efektua Über das farbige Licht der Doppelsterne und einige andere Gestirne des Himmels[1] (Izar bitar eta beste astroen argiaren koloreari buruz) tratatuan proposatu zuen 1842an, izar bitarren koloreak aztertzen ari zela. Hiru urte geroago, 1845ean Christoph Hendrik Diederik Buys Ballot[2] zientzialari nederlandarrak Doppler-ek proposatutako hipotesia ikertu zuen soinu-uhinen kasurako. Behatzailearengana hurbiltzen den iturri batek igorritako soinuaren tonua urruntzen denarena baino altuagoa dela ondorioztatu zuen.
Doppler efektua eguneroko bizitzan erabiltzen da, adibidez, ibilgailuen abiadura neurtzeko edo kiroletan piloten abiadura neurtzen duten gailuetan. Medikuntzan ere oso erabilgarria da; Izan ere, ultrasoinuen teknika Doppler efektuan oinarrituta dago.[3]
Doppler efektu klasikoa
[aldatu | aldatu iturburu kodea]Demagun ingurune batean uhin-iturri bat eta detektagailu bat higitzen ari direla eta abiaduraz hurrenez hurren. Kalkuluak errazteko, demagun bi abiadurak posizio erlatiboaren norabidean egongo direla, baina positiboak zein negatiboak izan daitezkeela. Soinuaren abiadura () ere kontuan hartuko dugu. Askotan, baina ez beti, soinu-uhinak interesatzen zaizkigu: iturria bozgorailu bat izan daiteke, detektagailua entzulearen belarria eta ingurunea airea.
Formula orokorra
[aldatu | aldatu iturburu kodea],[4]
non
.
Demagun anbulantzia bat guregana hurbiltzen ari dela. Kasu horretan, entzungo dugun sirenaren frekuentzia gero eta handiagoa izango da. Hori erraz ikus daiteke formulan. Iturria hurbiltzen denean, izendatzailea txikitu egingo da eta, beraz, entzungo dugun frekuentzia handiagoa izango da. Kontrako kasuan, izendatzailea handitu egingo da, eta entzungo dugun frekuentzia txikiagoa izango da.
Kasuak:
[aldatu | aldatu iturburu kodea]Demagun pertsona bat bere autoan dagoela. Urrunetik anbulantzia bat dator sirena piztuta daramala. Har dezagun anbulantzia iturritzat eta autoan dagoen pertsona hartzailetzat. Dauden kasuak ikusiko ditugu:
Hartzailea geldirik eta iturria mugimenduan
[aldatu | aldatu iturburu kodea]Kasu honetan, erraz ikus dezakegu hartzailearen abiadura nulua izango dela eta, beraz, entzungo den frekuentziaren aldaketa anbulantziaren abiaduraren eta noranzkoaren menpe egongo dela:
,
non ikurra iturria hartzailearengana hurbiltzen denean erabiliko dugun eta, ikurra, hartzailearengandik urruntzen denean.
Hartzailea mugimenduan eta iturria geldirik
[aldatu | aldatu iturburu kodea]Aurreko kasuaren antzekoa dugu hau baina, oraingoan, iturria da geldirik dagoena eta, hartzailea, mugimenduan dagoena. Beraz, iturriaren abiadura nulua izango da.
,
non ikurra hartzailea iturritik urruntzen denean erabiliko dugun eta, ikurra, iturrira hurbiltzen denean.
Biak mugimenduan
[aldatu | aldatu iturburu kodea]Azken kasuan, biak mugimenduan ditugu. Lau azpikasu bereiziko dira:
Hartzailea iturritik urrundu eta iturria hartzailearengana hurbiltzen denean
[aldatu | aldatu iturburu kodea].
Iturria hartzailearengandik urrundu eta hartzailea iturrira hurbiltzen denean
[aldatu | aldatu iturburu kodea].
Biak elkarrengana hurbiltzen direnean
[aldatu | aldatu iturburu kodea].
Biak elkarrengandik urruntzen direnean
[aldatu | aldatu iturburu kodea].
Adibidea
[aldatu | aldatu iturburu kodea]Demagun anbulantzia bat iparraldera doala 33.5 m/s-ko abiadurarekin; haren sirenaren soinuaren frekuentzia 400 Hz-koa da. Kalkulatu zenbatekoa izango den hegoalderantz doan pertsona batek entzungo duen frekuentzia, haren autoaren abiadura 24.6 m/s-koa bada:
a) Autoa eta anbulantzia elkarrengana hurbiltzen direnean
Kasu honetan, , eta . Hasierako frekuentzia ere datua da, . Beraz, 3.3 ataleko formula erabiliz,
.
Hori izango da hartzailearengana heltzen den frekuentzia.
b) Autoa anbulantziatik urruntzen denean
Oraingoan, 3.4 ataleko formula erabiliko dugu, eta aurreko ataleko datu berberak.
.
Doppler efektu erlatibista
[aldatu | aldatu iturburu kodea]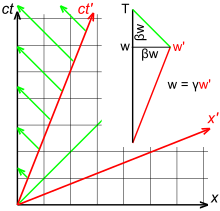
Erradiazio elektromagnetikoaren iturri baten maiztasun propioa (iturriaren sisteman neurtzen den maiztasuna) ν bada, iturriarekiko higitzen ari den behatzaileak beste maiztasun bat (ν′) neurtuko du. Fenomeno hori Doppler-ek aztertu zuen lehenengoz 1842an, eta Fizeau-k 1849an.[5]
OX ardatza higidura erlatiboaren norabidean aukeratzen badugu, iturriaren sisteman fotoiaren energia izango da eta, momentu linealaren osagai bakarra, . Era berean, behatzailearen sisteman, energia izango da eta, momentu lineala, . Beraz, honela idazten dira Lorentz-en transformazioak kasu honetan:
.
Ekuazio bietatik ondorio bera lortzen da:
.
Iturria eta behatzailea elkarrengandik urruntzen direnean, eta eta, beraz, behatzaileak neurtzen duen maiztasuna harena baino txikiagoa da: gorriranzko lerrakuntza dugu, zeren argi ikusgaiaren kasuan iturrian urdina den argia maiztasun txikiagoko argi gorri moduan ikusten baitu behatzaileak. Behatzailea eta iturria elkarrengana hurbiltzen direnean eta urdinerazko lerrakuntza gertatzen da: .
Erreferentziak
[aldatu | aldatu iturburu kodea]- ↑ 1935-, Eden, Alec,. (1992). The search for Christian Doppler. Springer-Verlag ISBN 0387823670. PMC 25833300..
- ↑ Nicolas., Witkowski,. (2007). Una historia sentimental de las ciencias. Siglo XXI ISBN 9789871220779. PMC 301796432..
- ↑ (Gaztelaniaz) «Efecto Doppler: en qué consiste y qué aplicaciones tiene» Factoría de Ingenieros 2016-04-11 (Noiz kontsultatua: 2018-03-22).[Betiko hautsitako esteka]
- ↑ D., Young, Hugh. (2009). Física universitaria. (12a ed. argitaraldia) Addison-Wesley ISBN 9786074422887. PMC 689254268..
- ↑ María., Aguirregabiria, Juan. (2004). Mekanika klasikoa. Universidad del País Vasco ISBN 8483736314. PMC 932541663..





























