K auzokide hurbilenak
| Ikasketa automatikoa eta Datu-meatzaritza |
|---|
 |
k auzokide hurbilenen metodoa (ingelesez: k-nearest neighbors edo K-NN) datu-meatzaritzan eta ikasketa automatikoan sailkapen gainbegiratua egiteko metodo bat da. Entrenamendurako kasuen artean, k auzokide hurbilenetan oinarritzen da kasu berrien sailkapena egiteko. Hurbileneko k auzokideen klase-aldagaiaren balioa aztertu eta sarrien agertzen den klasea esleitzen zaio kasu berriari.
k-NN algoritmoak ikasketa nagia edo alferra (lazy learning) egiten duela esaten da, ez duelako eredu bat induzitzen ikasketa-fasean; entrenamendurako datu-basetik eredu bat sortu beharrean, datu-base berarekin egiten da kasu berriaren klase-aldagaiaren iragarpena test-fasean.
Metodoa sinplea eta intuitiboa da; distantzien kalkuluan oinarritzen da. Algoritmoaren bertsiorik sinpleenean k auzokide hurbilenen klaseei tratamendu bera ematen zaie, baina badira algoritmoaren aldaera desberdinak auzokideen artean bereizketa egiteko, kasu berrira duten distantziaren arabera garrantzia maila desberdina emateko, adibidez[1].
Algoritmoa[aldatu | aldatu iturburu kodea]

Gainbegiratutako sailkapenerako algoritmo bat da k-NN[2]. Abiapuntua kasuz osatutako datu-base bat da, modukoa, non bektoreak kasua deskribatzen duen eta den klase-aldagairako haren etiketa edo balioa. Kasuei erreferentzia egiteko, adibide edo prototipo hitzak ere erabiltzen dira. Datu-basetik abiatuz, gainbegiratutako sailkapenerako algoritmoek normalean eredu bat induzitzen badute ere, k-NN algoritmoa berezia da, ez baitu halakorik egiten; horregatik esaten da ikasketa nagia edo alferra egiten duela, ez duelako berezko entrenamendu- edo ikasketa-faserik.
Sailkatze- edo test-fasean, bektorearen bidez deskribatutako kasu berri bat iristen denean, datu-baseko kasu guztietara duen distantzia kalkulatu behar da, distantzia euklidearra normalean, ondoren kasuak distantzia txikienetik handienera ordenatu eta erabiltzaileak definitutako k balioaren arabera hurbilen dauden k kasuak aurkitzeko. Auzokide hurbilenak diren k kasu horien klasea begiratu eta sarrien agertzen den klasea esleitzen zaio kasu berriari. Eredurik erabili gabe, test-fasean kalkulatutako distantzietan oinarritzen da k-NN algoritmoa kasu berriaren klase-aldagaiaren iragarpena egiteko.
Irudian k-NN algoritmoaren adibide bat ikus daiteke. Datu-base horretan kasu daude: horietako 6 "karratu urdin" klasekoak dira eta gainerako 5ak "triangelu gorri" klasekoak. Kasuak planoan adierazita daude, hau da, kasu bakoitza adierazten duen bektoreak bi osagai ditu. Zirkunferentzia berde batez adierazita dator sailkatu behar den kasu berria, bektorearen bidez deskribatuta datorrena. Hura "karratu urdin" klasekoa edo "triangelu gorri" klasekoa den erabakitzeko, datu-baseko 11 kasuetarako distantzia kalkulatu behar da. Irudiko zirkunferentziaren erradioak distantzia hori erakusten du. Erabiltzaileak k=3 balioa aukeratzen badu, 3-NN algoritmoak 3 auzokide hurbilenen klaseak erabiliko ditu iragarpena egiteko; "karratu urdin" klaseko bakarra eta "triangelu gorri" klaseko bi daudenez, sarrien agertzen den klasea esleituko dio kasu berriari: "triangelu gorri" klasea. k=5 balioa aukeratzen badu, "triangelu gorri" klaseko 2 eta "karratu urdin" klaseko 3 daudenez 5 auzokide hurbilenak biltzen dituen kanpoko zirkuluan, "karratu urdin" klasea esleituko zaio kasu berriari.
k-NN algoritmoa erabiltzean, batzuetan "berdinketa" kasuak gertatzen dira: datu-baseko hainbat kasu distantzia berera egotea kasu berritik, hurbileneko auzokideen artean sarrien agertzen diren klaseetan kasu kopuru bera egotea, etab. Halakoak ebazteko estrategia desberdinak proposatu izan dira. Oinarrizko k-NN algoritmoaren aldaerak lortzen dira horrela.
Distantzia euklidearra[aldatu | aldatu iturburu kodea]
k-NN algoritmoak prototipoen edo kasuen arteko distantziak kalkulatu behar ditu. Normalean distantzia euklidearra erabiltzen da. n-dimentsioko espazio euklidear batean, eta bi punturen arteko distantzia euklidearra horrela definitzen da:
Hortaz, bektoreak deskribatutako kasu berri bat k-NN algoritmoaren bidez sailkatzeko, haren eta datu-baseko kasu guztien arteko distantziak kalkulatu behar dira, .
Kasuaren deskribapena bi aldagai iragarlez ematen denean, eta bi puntuan planoan adieraz daitezke, eta distantzia euklidearraren kalkulua horrela geratzen da:
emateko.
Distantziaren definizio hori Pitagorasek emandako teorematik eta gerora Euklidesek egindako formalizazio lanetik eratorriak dira: geometria euklidearra.
k parametroa[aldatu | aldatu iturburu kodea]
k-NN algoritmoa erabiltzeko, k parametroaren balioa finkatu behar da. Oro har, ez dago k-ren baliorik egokiena aukeratzeko metodorik eta ez da egia zenbat eta balio altuagoa aukeratu orduan eta sailkapen hobea lortuko denik. Datu-basearen arabera, k-ren balio desberdinetarako algoritmoaren eraginkortasuna aldatu egiten dela ikusi da. Gehienetan, k-ren balio handiek sailkapenaren zarata txikiagotzen dute, baina klaseen arteko mugak ez dira hain argiak izaten. Hori dela eta, modu esperimentalean aukeratu behar izaten da k-ren balioa. Normalean, 3 eta 7 arteko balio bakoitiak aukeratzea gomendatzen da. k=1 aukeratzen denean, algoritmoak "auzokide hurbilenaren algoritmo" izena hartzen du.
Algoritmoaren aldaerak[aldatu | aldatu iturburu kodea]
Algoritmoaren oinarrizko ideiatik abiatuz, posible da k-NN algoritmoaren aldaera desberdinak sortzea. Arrazoi desberdinak egon daitezke algoritmoaren hainbat xehetasun aldatuz aldaera desberdinak sortzeko. Atal honetan aldaera horietako batzuk azaltzen dira.
Bermerik gabekoak baztertuz[aldatu | aldatu iturburu kodea]
k-NN algoritmo orokorraren arabera, k auzokideen artean sarrien agertzen den klasea esleitzen zaio kasu berriari. Baina sailkatze-problema batzuetan horrek ez du nahikoa berme eskaintzen kasu berriaren iragarpena egiteko. Hori dela eta, atalase bat finka daiteke eta auzokide hurbilenen artean sarrien agertzen den klasea atalaseak adierazitako kopurua adina aldiz agertu beharko da, gutxienez, iragarpena egiteko. Hala ez den kasuetan, kasu berria sailkatu gabe uzten da. Atalaseari k parametroaren balio bera ematen zaionean, hau da, gertuko auzokide guztiak klase berekoak (guztien adostasuna) izatea eskatzen denean, bermearen maila maximoa lortzen da.
Adibidez, izan bedi bi klase ezberdinetan banatutako 100 kasuz osatutako entrenamendurako datu-base bat eta k=5 parametroa. Erabiltzaileak atalase desberdinak finka ditzake, lortu nahi duen bermearen arabera: atalasea 4 balioan finkatzen badu, 5 auzokide hurbilenen artetik gutxienez 4 klase berekoak badira egingo du klasearen iragarpena 5-NN algoritmoak. Atalasea 3 balioan finkatzen badu, lortu beharreko bermearen maila jaitsiko du, nahikoa izango baita 5etik 3 klase berekoak izatea iragarpena egiteko. Bermerik altuena atalasea 5 balioarekin finkatuz lortuko du: auzokide guztien adostasuna.
Auzokide hurbilenen arteko bereizketa[aldatu | aldatu iturburu kodea]
k-NN algoritmo orokorraren arabera, k auzokide hurbilenen artean sarrien agertzen den klasea esleitzen zaio kasu berriari, auzokide horien artean inolako bereizketarik egin gabe. Gerta daiteke kasu berritik hurbilen dauden auzokide horien artean sarrien agertzen den klasekoak urrutien daudenak izatea. Irudiko adibidean, k=5 aukeratzen den kasuan argi ikusten da "triangelu gorri" klaseko 2 eta "karratu urdin" klaseko 3 daudenez 5 auzokide hurbilenen artean, algoritmo orokorrak "karratu urdin" klasearen iragarpena egiten duela kasu berriarentzat, nahiz eta "karratu urdin" klaseko hiruak "triangelu gorri" klasekoak baino urrutiago egon.
k auzokide hurbilenak distantziaren arabera bereizi nahi badira, estrategia desberdinak erabil daitezke:
- Batez besteko distantzia erabiltzea. Auzokideak klaseka multzokatu eta batez bestean kasu berrira zein distantziara dauden kalkulatzen da. k-NN algoritmoak batez bestean distantzia txikienera dagoen klasea esleituko dio kasu berriari.
- Klaseen ordezkariak erabiltzea. Auzokideak klaseka multzokatu eta klase bakoitzerako ordezkari bat aukeratzen da. Gehienetan klase bakoitzeko barizentrotik (klase bereko kasuen "zentrotik") hurbilen dagoen kasua hautatzen da ordezkari moduan. k-NN algoritmoak distantzia minimora dagoen ordezkariaren klasea esleituko dio kasu berriari.
- Auzokideak haztatzea edo "Weighted k-NN"[3][4]. auzokideak distantziaren arabera haztatu egiten dira, . Haztapenak garrantzia maila desberdina ematen die kasuei, kasu berritik gertuen daudenek haztapen altuagoa jasoko dutelarik. Distantziaren araberako haztapena modu desberdinean defini daiteke:
Auzokide hurbilenak klaseka elkartu eta haien haztapenen batura egiten da. Batura handieneko klasea esleitzen zaio kasu berriari.
Aldagai iragarleak haztatzea[aldatu | aldatu iturburu kodea]
Sailkapen-problemetan, prototipoak osagaiko bektoreen bidez deskribatzen dira. Osagai horietako bakoitza ezaugarri bati buruzko informazioa ematen duen aldagai iragarle baten balioa da. aldagai iragarle horiek ematen duten informazioa ez da garrantzia maila berekoa izaten, klase-aldagaiaren iragarpenean.
Adibide bat jartzearren, datu-baseko kasuak osasun-zentro bateko pazienteak badira, bektoreek pazienteei buruzko informazioa emango dute: adina, egindako probaren baten emaitza, etab. Medikuak gaixotasunei buruz duen ezagutza erabiltzen du pazientearen sintomak aztertuz diagnostikoa egiteko; klase-aldagaia da diagnostikoa gordetzen duena. Antzeko egoeran dauden pazienteen (auzokide hurbilenen) diagnostikoan oinarritzen da k-NN algoritmoa -ren iragarpena egiteko.
Antzeko egoeran dauden pazienteak aurkitzeko, garrantzitsua gertatzen da aldagai iragarle bakoitzak ematen duen informazioa neurtzea. Izan ere, sintoma batzuk oso erlazionatuta baitaude gaixotasunarekin baina datu-baseko beste datu batzuk ez dira esanguratsuak. Aldagai iragarleak haztatzeko beharra sortzen da, klase-aldagaiaren iragarpenean duten garrantziaren arabera.
Ezaugarri edo aldagai iragarle bakoitzaren garrantzia adierazten duen haztapena kalkulatu behar da. Kalkulatzeko modu bat aldagai iragarlearen eta klase-aldagaiaren elkarrekiko informazioaren neurria erabiltzea da:
izanik aldagaiaren balio posibleak eta izanik -ren etiketa posible guztiak.
Distantzia euklidear haztatuaren kalkulua bi aldagai iragarleren kasurako horrela geratzen da:
kasu berria izanik eta datu-baseko kasuak, .
Datu-baseko kasu kopurua murriztea[aldatu | aldatu iturburu kodea]
k-NN algoritmoa sailkapen gainbegiraturako metodo bat izateaz gain, aurre-prozesaketa fasean datu-baseko prototipo kopurua murrizteko erabil daiteke. Izan ere, ikasketa automatikorako erabili ohi diren datu-baseak oso handiak izaten dira, horrek dakarren konputazio-kostua altua izanik. Datu-basea arindu nahi izaten da, soberan egon litezkeen kasuak ezabatuz. Noski, ez dira datu-basetik ezabatu nahi klaseen definizioan garrantzitsuak diren kasuak. Horrela, datu-basetik zein prototipo ezabatuko diren erabaki behar da.
k-NN algoritmoan oinarritutako bi metodo daude: Hart-en kondentsazioa eta Wilson-en edizioa.
Hart-en kondentsazioa[aldatu | aldatu iturburu kodea]
Hart-ek 1968. urtean argitaratu zuen "The condensed nearest neighbor rule"[5] izenburua duen artikulu zientifikoa. Datu-base bat izanik, prototipo batzuk ezabatuz datu-base murriztua lortzea da helburua, jatorrizko datu-baseko kasuek islatutako klaseen banaketa ahalik eta ondoen mantenduz. Proposatzen den algoritmoak bi zerrenda erabiltzen ditu: STORE zerrenda, datu-basean mantenduko diren prototipoak gordeko dituena eta GRABBAG zerrenda, ezabatuak izateko aukeratutako prototipoak dituena. Kasuak ezabatuz arindu nahi den datu-basea entrenamendurako erabiliko dena denez, prototipo guztien klasea ezaguna da.
Honakoak dira algoritmoaren urratsak:
- Datu-baseko lehenengo kasua STORE zerrendan sartu.
- Datu-baseko bigarren kasuaren klasearen iragarpena egin k-NN erabiliz STOREko kasuetan oinarrituz. Sailkapena zuzena bada, kasua GRABBAG zerrendan sartu, bestela STOREn sartu.
- Modu berean segi datu-baseko kasu guztiekin.
- Datu-baseko kasu guztiak aztertu ondoren, GRABBAG zerrendakoekin prozedura errepikatu behin eta berriz. Prozesuaren amaiera bi modutara lor daiteke:
- GRABBAG zerrenda hutsa dago, denak STOREn daude.
- Iterazioren batean GRABBAG zerrendako kasu guztiak aztertu ondoren, bat bera ere ez da STORE zerrendara pasa; zerrendak egonkortu dira.
- GRABBAG zerrendako kasuak datu-basetik ezabatuko dira.
Metodo honen arabera, k-NN algoritmoak egindako iragarpena eta kasuaren klase erreala berdinak badira, prototipoa GRABBAG zerrendan sartzen da ezabatua izateko. Izan ere, gertuko bi auzokideak klase berekoak izanik, biak gorde beharrik ez dagoela interpretatzen da. Hart-en kondentsazioarekin klase desberdinekoak diren eta haien artean gertu dauden prototipoak gordetzen dira, horiek daudelako klaseen arteko mugan. STORE zerrendan hasieran prototipo bakarra dago, datu-baseko lehenengoa, eta iterazioak aurrera doazen moduan kasuak sartuko dira bertan. Horregatik errepikatu behar da prozesua behin eta berriz, k-NN algoritmoak STORE zerrenda desberdinetan bilatuko dituelako auzokide hurbilenak eta horien arabera iragarpenak alda daitezkeelako.
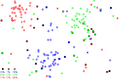
1.Irudian hasierako datu-basea osatzen duten 180 kasuak ikusten dira, bi aldagai iragarleren bidez deskribatuta datozenak. Prototipoak hiru klasetakoak dira, "gorri", "urdin" eta "berde", eta klase bakoitzetik 60 daude. 2. eta 3 irudietan hasierako datu-basean klaseak nola banatzen diren ikusten da, iragarpenak 1-NN eta 5-NN erabilita egin dira, datu-base osoaren gainean. 4.irudian Hart-en kondentsazioa egin ondoren geratu den datu-base murriztua ikusten da eta 5.irudian adierazten da datu-base murriztuan nola geratu den klaseen banaketa, 1-NN aplikatuta.
-
1.Irudia: Datu-basea
-
2.Irudia: Klaseen banaketa (1-NN-rekin)
-
3.Irudia: Klaseen banaketa (5-NN-rekin)
-
4.Irudia: Datu-base murriztua
-
5.Irudia: Klaseen banaketa datu-base murriztuan (1-NN-rekin)
Ikus daiteke 2. eta 5.irudien artean ez dagoela ezberdintasun handirik. Hortaz, datu-basea kasuz arintzea lortu da, beti ere klaseen arteko banaketa oso antzekoa mantenduz. Horri esker, gainbegiratutako sailkapeneko test-fasea azkarragoa izango da, datu-basea arindu denez distantzia kopuru txikiagoa kalkulatu beharko delako; asmatze-tasa antzera mantenduko da.
Wilson-en edizioa[aldatu | aldatu iturburu kodea]
Metodo honek Hart-en kondentsazioaren metodoaren helburu bera du: datu-base bat izanik, prototipo batzuk ezabatuz datu-base murriztua lortzea, jatorrizko datu-baseko kasuek islatutako klaseen banaketa ahalik eta ondoen mantenduz. Wilson-ek argitaratu zuen 1972an artikulu zientifiko batean "Asymptotic Properties of Nearest Neighbor Rules Using Edited Data" izenburupean[6]. Honakoak dira urratsak:
- Errepikatu guztietarako:
- Datu-baseko kasuen artean k auzokide hurbilenak aurkitu.
- kasuari bere auzokide hurbilenen artean sarrien agertzen den klasea esleitu.
- Esleitutako klasea eta klase erreala bat ez datozen kasu guztiak datu-basetik ezabatu.
Kasu honetan, Hart-en kondentsazioaren metodoan ez bezala, gertueneko direnen klaseak desberdinak direnean ezabatzen dira kasuak datu-basetik. Horrela lortu nahi da klaseak haien artean ondo bereiztea, hain zuzen ere klaseen arteko mugetan dauden kasuak ezabatuz.
Erreferentziak[aldatu | aldatu iturburu kodea]
- ↑ (gazteleraz) Sierra Araujo, B. Aprendizaje automático : conceptos básicos y avanzados : aspectos prácticos utilizando el software WEKA. Pearson 2006 ISBN 84-8322-318-X. PMC 629686982. (Noiz kontsultatua: 2019-12-23).
- ↑ (ingelesez) Dasarathy, Belur V. Nearest neighbor (NN) norms : nn pattern classification techniques. IEEE Computer Society Press 1991 ISBN 0-8186-8930-7. PMC 22272787. (Noiz kontsultatua: 2019-12-23).
- ↑ (Ingelesez) «Weighted K-NN» GeeksforGeeks 2019-06-14 (Noiz kontsultatua: 2019-12-26).
- ↑ (Ingelesez) «Weighted k-nearest neighbors - Nearest Neighbors & Kernel Regression» Coursera (Noiz kontsultatua: 2019-12-26).
- ↑ (Ingelesez) Hart, P.. (1968-05). «The condensed nearest neighbor rule (Corresp.)» IEEE Transactions on Information Theory 14 (3): 515–516. doi:. ISSN 0018-9448. (Noiz kontsultatua: 2019-12-26).
- ↑ Wilson, Dennis L.. (1972-07). «Asymptotic Properties of Nearest Neighbor Rules Using Edited Data» IEEE Transactions on Systems, Man, and Cybernetics SMC-2 (3): 408–421. doi:. ISSN 0018-9472. (Noiz kontsultatua: 2019-12-26).
Ikus, gainera[aldatu | aldatu iturburu kodea]
Kanpo estekak[aldatu | aldatu iturburu kodea]
- (ingelesez) "A Simple Introduction to K-Nearest Neighbors Algorithm"
- (ingelesez) "Model Selection, Tuning and Evaluation in K-Nearest Neighbors"
- (ingelesez) "Introduction to k-Nearest Neighbors: A powerful Machine Learning Algorithm (with implementation in Python & R)"