Bilketa (multzo-teoria)

A eta B bi multzoen bilketatik A ∪ B beste multzo bat sortzen da, bildura deiturikoa, A eta B multzoetako elementu guztiak dituena.

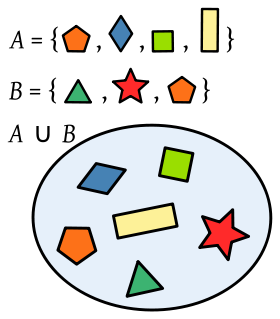
Matematikan, multzo-teoriaren barruan, bilketa multzoen artean definitzen den eragiketa bat da. Eragiketa horrek multzo bat sortuko du, bildura multzoa deiturikoa, zeinek multzoetako elementu guztiak biltzen dituen. Bilketa adierazteko, $\cup$ ikurra erabiltzen da, eta bil irakurtzen da. Adibidez, A eta B multzoetako elementuen bilketa honela adierazten da:

$A\cup B$ , (A bil B irakurtzen da).

Sinboloa	Izena	Esanahia	Adibideak
	Ahoskera
	Adarra
∪	Bilketa	$A\cup B$ (A eta B multzoen bildura, hots, A-koak edo B-koak edo bietakoak diren elementuen multzoa) «a bil be»	$A\subseteq B\iff A\cup B=B$
	«... bil ...»
	Multzo-teoria

Multzoen bilketaren propietateak

Propietate idenpotentea

$A\cup A=A$

Elementu neutroa

$A\cup \phi =A$

Trukatze-legea

$A\cup B=B \cup A$

elkartze-legea

$A\cup B \cup C=(A\cup B )\cup C=A\cup (B \cup C)$

Multzo osagarrien batuketa

$A$ multzo bat eta $\overline{A}$ bere osagarria $R$ multzoarekiko baditugu, $A$ eta $\overline{A}$ multzoen bildura $R$ da.

$A \cup \overline{A} = R$

Azpimultzoen bilketa

A eta B multzoak baditugu, non $A\supset B$ (A-k parte du B), orduan $A \cup B=A$

Ikus, gainera

• Bilketa (probabilitatea)