Lauki
| Laukia | |
|---|---|
 Sei lauki mota | |
| Aldeak | 4 |
| Schläfli sinboloa | {4} (karratua) |
| Azalera | hainbat metodo; begiratu ondoan |
| Barne-angelua | 90° (karratua) |
Geometrian, laukia irudi lau bat da, lau alde zuzen, lau erpin eta bi diagonal dituena eta barne-angeluen batura 360º osatzen dute:
Lauki guztiak lauangeluarrak dira eta definizioa hau lau angelu dituzten poligonoetara aplikatzen da.
Laukiaren elementuak[aldatu | aldatu iturburu kodea]
Laukia osatzen duten elementuak honako hauek dira:
- 4 erpin: laukia osatzen duten aldeen elkargune puntuak dira.
- 4 alde: Jarraian dauden bi erpinek mugatzen duten zuzenkia da.
- 2 diagonal: Jarraian ez dauden bi erpin elkartzean sortzen den zuzenkia da.
- 4 barne angelu: Bi aldeek eta erpin komun batek osatzen dituzte.
- 4 kanpo angelu: Aldeen luzapenak osatzen dituzte.
Lauki-motak[aldatu | aldatu iturburu kodea]

- Lauki ganbilak: barne angelu guztiak 180º baino txikiagoak dira (erpin guztiak kanpora).
- Paralelogramoa: aurrez aurreko aldeak paraleloak dituena. Horren ondorioz, aurrez aurreko aldeak eta angeluak ere berdinak dira. Haien adibide batzuk:
- Karratua: lau aldeak berdinak eta lau angeluak zuzenak dituena.
- Laukizuzena: lau angelu zuzen eta aurrez aurreko aldeak berdinak dituena.
- Erronboa: lau aldeak berdinak dituen baina angelu zuzenik ez duena.
- Erronboidea: aurrez aurreko aldeak soilik berdinak dituen eta angelu zuzenik ez duena.
- Trapezioa: soilik bi alde paralelo dituena. Hiru mota daude:
- Trapezio zuzena: bi angelu zuzen ditu.
- Trapezio isoszelea: paraleloak ez diren aldeak luzera berdinekoak dira.
- Trapezio eskalenoa: paraleloak ez diren aldeak luzera desberdinekoak dira.
- Trapezoide: elkarren arteko alde paralelorik ez duena.
- Paralelogramoa: aurrez aurreko aldeak paraleloak dituena. Horren ondorioz, aurrez aurreko aldeak eta angeluak ere berdinak dira. Haien adibide batzuk:
- Lauki ahurrak: angelu bat 180º baino handiagoa da.
Taxonomia[aldatu | aldatu iturburu kodea]
Laukien taxonomiaren adierazgarri den grafikoan definizio orokorretatik definizio zehatzetara gezien norabidea jarraitzen da.
Horrela laukia definitu egiten da lau aldek mugatzen duten poligonoan, zehaztasunik gabe, lauki konposatu eta sinpleak ezberdintzeko.
Lauki konplexu batean bere bi alde moztu egiten dira. Lauki sinple batean aldeak ez dira gurutzatzen.
Lauki sinpleak bi motatakoak izan daitezke:
- Ahurra: Lauki ahur batean gutxienez barne angelu batek 180º baino gehiago neurtzen du.
- Ganbila: Lauki ganbil batean ez ditu barne angelurik 180º baino gehiago neurtzen dutenik. Ganbilak honela bereizten dira:
1. Lauki ziklikoa: Erpinetik zirkunferentzia bat pasatzen baldin bada egin daiteke.
2. Lauki ukitzailea: Alde guztietan zirkunferentzia ukitzaile bat pasatzen bada egin daiteke.
3. Trapezioak: Bi alde paralelo baldin badituzte. Ezberdintzen dira:
3.1. Erronboide: Paralelogramoen kasu orokorrena izanda, bi aldek paraleloak badira bi eta bi.
3.2. Trapezio angeluzuzena: Alde perpendikular bat dute oinarriarekiko.
3.3. Trapezio isoszelea: Bere alde ez paraleloak berdinak dira. Trapezio hau ere ziklikoa da.
Lauki bat ziklikoa eta ukitzailea denean lauki bizentroduna dela esaten da. Deltoidea ukitzailea da bi alde pare berdinekin.
Trapezio isoszele baten kasu berezi bat sortzen da oinarri baten luzera eta aldeen luzera berdina denean, beraz hiru alde berdinen trapezioa osatzen da.
Laukizuzena propietate hauek betetzen ditu:
· 1. Paralelogramoa: bere kontrako aldeak paraleloak dira.
· 2. Trapezio angeluzuzena: bi aldeak perpendikularrak dira oinarriarekiko.
· 3. Trapezio isoszelea: Luzera berdinak dituzten oinarri ez eratzaileak diren aldeak dira.
Era berean, egiaztatu daiteke erronboa deltoide paralelogramo bat dela, bien propietateak betetzen dituelako.
Azkenik, kontuan hartu daiteke laukia; erronboa , laukizuzena, bi alde berdin eta bizentroduna dela.
Formulak[aldatu | aldatu iturburu kodea]
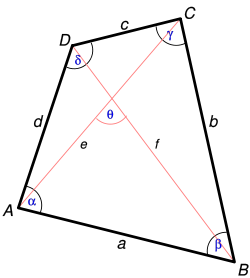
lau erpinak (A, B, C, D) eta bi diagonalak (e, f).
- Barne angeluen batura 360° da (gradu sexagesimal) edo 2π radian.
- Lauki baten azalera hainbat modutan kalkula daiteke:

![thumb[Betiko hautsitako esteka]](http://upload.wikimedia.org/wikipedia/commons/0/09/Tangentenviereck.png)






