Goldbachen aieru
Zenbakien teorian Goldbachen aierua matematikako problema ireki eta aieru antzinakoenetako bat da. Batzuetan, zientzia honen historian problemarik zailenentzat hartzen da. Honakoa da bere formulazioa:
| « | "2 baino handiagoa den zenbaki bikoiti oro bi zenbaki lehenen arteko batuketa bezala idatz daiteke. Christian Goldbach (1742 | » |
Zenbaki lehen bera bi aldiz erabil daitekeela ere aipatu behar da.
Adibidez: 4 = 2+2, 6 = 3+3, 8 = 3+5, 10 = 3+7, 12 = 5+7, 14 = 3+11
Historia
[aldatu | aldatu iturburu kodea]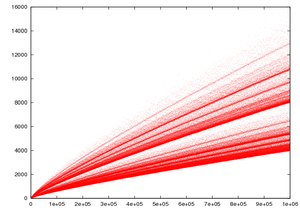
Descartesek ezagutzen zuen aierua. Jarraian agertzen den baieztapena aurrekoaren baliokidea da, eta jatorrian Goldbachek Leonhard Eulerri zuzendutako gutun batean aipatu ziona da.
| « | 5 baino handiagoa den zenbaki oso oro hiru zenbaki lehenen batuketa bezala idatz daiteke. | » |
Aieru hau zenbakien teoriko askok ikertu dute, eta ordenagailuek 1018 baino txikiagoak diren zenbaki bikoiti guztientzat frogatu dute. Matematikari gehienek aieruak egia dioela uste dute, eta, nagusiki zenbaki naturalen artean zenbaki lehenen banaketa probabilistikoaren kontsiderazio estatistikoetan oinarritzen dira: zenbaki bikoitia zenbat eta handiagoa izan "probableago" bihurtzen da bi zenbaki lehenen arteko batuketa bezala idatzi ahal izatea.
Zenbaki bikoiti oro modu minimoan gehienez ere sei zenbaki lehenen arteko batuketa bezala idatz daitekeela ezagutzen da. Ivan Vinogradoven lan baten ondorio bezala, behar bezain handia den zenbaki bikoiti oro, gehienez ere lau zenbaki lehenen arteko batuketa bezala idatz daiteke. Gainera, Vinogradovek ia zenbaki bikoiti guztiak bi zenbaki lehenen arteko batuketa bezala idatz daitezkeela frogatu zuen (modu horretan idatz daitezkeen zenbaki bikoitien proportzioak 1erako joera izatearen zentzuan). 1966an Chen Jing-runek behar bezain handia den zenbaki bikoiti oro zenbaki lehen bat eta gehienez ere bi faktore lehen dituen zenbaki baten arteko batuketa bezala idatz daitekeela frogatu zuen.
Apostolos Doxiadisen Petros osaba eta Goldbachen aierua liburuarentzako publizitatea egiteko asmoz, Tony Faber britainiar editoreak 2000n aieru hau 2002ko apirila baino lehenago frogatzen zuen ingeles-hiztun orori milioi bat dolarreko saria eskaini zion. Baina inork ez zuen saria aldarrikatu.
Goldbachek zenbaki lehenen batuketari buruzko elkarren artean lotutako bi aieru formulatu zituen: Goldbachen aieru "indartsua" eta Goldbachen aieru ahula. Hemen eztabaidatzen dena aieru indartsua da, eta soilik Goldbachen aieru bezala aipatzen dena.
Aieru honen eragina izan duten lanak
[aldatu | aldatu iturburu kodea]Zinean
- Goldbachen aierua 2007ko espainiar filma den La habitación de Fermaten istorioko zati da.
- 2005eko Proof filmean ere agertzen da.
- Futuramaren bigarren filma den 2008ko Milioi Bat Bizkardun Piztian Hubert Fansworth irakasleak aieru hau aipatzen du.
Literaturan
- Petros osaba eta Goldbachen aierua bere osabak bere bizitza guztia aieru hau argitzen saiatzen eman zuen gazte baten bizitzari buruzko Apostolos Doxiadisen eleberri bat da.
Kanpo estekak
[aldatu | aldatu iturburu kodea]| Autoritate kontrola |
|
|---|
Datuak: Q485520
Multimedia: Goldbach's conjecture / Q485520