Matrize
- Artikulu hau matematikako adierari buruzkoa da, beste adierei buruz jakiteko, ikus Matrize (argipena).

Matematikan, matrizea zenbakiz osaturiko errenkada (edo zutabe) multzo laukizuzen bat da, beste matrize batekin batera batu eta biderkatu egin daitekeena. Adibidez, honakoa 2 errenkada eta 3 zutabe dituen matrizea da[1]:
Askotan, matrizeak ekuazio linealetako sistemak planteatu eta ebazteko erabiltzen dira. Halaber, aljebra linealaren funtsezko tresna dira eta horrela, aplikazio zabalak dituzte zientziaren arlo anitzetan, ekonomiatik (non errenkadaz errenkada herrialde ezberdinetan izandako gai andana baten ekoizpenak adieraz ditzaketen, esaterako) fisikara (hiru dimentsiotako kokapenak islatzen denean, adibidez).
Notazioa eta definizioak[aldatu | aldatu iturburu kodea]
m errenkada eta n zutabe dituen matrizea m × n matrizea dela esaten da. m eta n matrizearen dimentsioak dira. m eta n dimentsiotako matrize guztien multzoa M(m,n) idazten da.
Bi dimentsioetako bat, m edo n, 1 bada, matrizea bektore bat dela ere esan daiteke. m=1 denean, matrizea errenkada-bektore dela esaten da. n=1 denean, matrizea zutabe-bektorea dela esaten da.
i-garren errenkada eta j-garren zutabeko A matrize bateko elementua (i,j) elementua da eta ai,j adierazten da.
Horrela, m × n matrize bat honela adieraz daiteke: A = [ai,j]m×n, non (i=1, 2, ..., m; j=1, 2, ..., n).
Adibide gisa hartutako goiko matrizea honela adieraz daiteke, beraz:
Eta esate baterako,
Horrela, A matrize bateko elementuen kokapen orokorra hau izango da:
Matrize-eragiketak[aldatu | aldatu iturburu kodea]
Matrizeen artean eragiketa anitz defini daitezke. Matrizeak elkarren artean batu eta biderkatu egin daiteke. Eskalar batez biderkatu ere egin daitezke. Matrize bat irauli egin daiteke. Matrize baten alderantzizko matrizea ere definitzen da.
Oinarrizko eragiketak[aldatu | aldatu iturburu kodea]
| Eragiketa | Definizioa | Adibidea |
|---|---|---|
| Batuketa | Dimentsio bereko A eta B matrizeen batuketa egiteko euren elementuen batuketa egiten da, elementuz elementu. |
|
| Biderketa eskalarra | k zenbaki baten (aljebran, k zenbakia eskalar bat dela esaten da) eta A matrize baten biderketa A matrizeko elementu guztiak k eskalarraz biderkatuz egiten da. |
Matrizeen biderketa[aldatu | aldatu iturburu kodea]
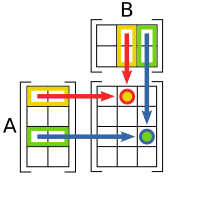
Bi matrizeen biderketa lehenengo biderkagai den matrizearen zutabe kopurua bigarren biderkagaia den matrizearen errenkada kopuruarekin bat badator bakarrik definitzen da. Horrela A m × n dimentsioko matrizea bada, eta B n × p matrizea bada, AB biderkadura-matrizea m × p dimentsiokoa da eta bere ab elementuak honela kalkulatzen dira, A eta B matrizeetako a eta b elementuak harturik:
Adibidez,
Esate baterako, azpimaratutako 1 elementua honela kalkulatzen da:
- .
Matrizeen biderketen propietateak[aldatu | aldatu iturburu kodea]
Izan bedi A,B,C matrizeak, gorputzean oinarrituak. Orduan, hurrengoko propietateak betetzen dira (matrizeen arteko biderketa existitzen bada)
- Elkartze-propietatea:
- Banatze-propietatea (eskuinetik, matrizeen gehiketarekiko):
- Banatze-propietatea (eskuinetik, matrizeen gehiketarekiko):
Matrizeen arteko biderketa ez da trukakorra, izan ere, horrek ondorioztatuko luke bi aplikazio linealen arteko konposaketa ere trukakorra izatea eta hori ez da orokorrean egia. Hala ere, existitzen dira kasu partikular batzuk non propietate trukakorra betetzen den, baina, esan bezala, ez da orokorrean betetzen.
Matrizeen determinantea[aldatu | aldatu iturburu kodea]
matrize karratuen gainean definitutako eragiketa berezi bat da, honela definitzen dena:
Bat ordenako matrize baten determinantea da.
Bi ordenako matrize baten determinantea
Hiru ordenako matrize baten determinantea Sarrusen erregelaren bitartez kalkulatzen da:
Ordena altuagoko determinantea kalkulatzeko, Laplaceren teoremak metodo bat aurkezten du, eragiketa ordena txikiagoko determinanteen arteko batuketa eta kenketetara sinplifikatzen duena (goian ikusi dugu hauek nola kalkulatu). Prozesu hau behar bezain beste errepikatuz, nahi bezain beste ordena txikiko determinante askoren kalkulura murriztu dezakegu problema.
Matrizeei lotutako beste hainbat kontzeptu[aldatu | aldatu iturburu kodea]
Matrize baten heina[aldatu | aldatu iturburu kodea]
Matrize baten heina, matrize hori osatzen duten zutabe edo errenkada linealki-independiente edo askeen kopuru maximoa da eta rg(A) adierazten da (A matrize bat izanik). Zutabe-heina (linealki-askeak diren zutabe kopurua) eta errenkada-heina (linealki-askeak diren errenkada kopurua) beti datoz bat.
Gainera, matrize baten heina bat dator matrize horren zutabe edo errenkadek sortzen dituzten espazio bektorialen dimentsioarekin. Beraz, A n zutabe eta m errenkadadun matrizearen heina zenbaki positibo bat izango da, m eta n-ren minimoaren txikiagoa edo berdina:
Matrize iraulia edo transposatua[aldatu | aldatu iturburu kodea]
matrize baten iraulia (non ez da zertan gorputz bat izan), matrize bat izango da non . Modu informalago batean, esan genezake matrize iraulia lortzen dugula matrize baten errenkadak eta zutabeak elkarrekin trukatuz. Adibide zehatz bat ikus dezagun:
Izan bedi orduan, matrize horren iraulia izango litzateke.
Matrizeen transposizioak hurrengoko propietate hauek betetzen ditu (orain bai, gutxienez eraztun trukakorra izan beharko da gutxienez):
matrizea aplikazio lineal baten errepresentazioa bada, orduan matrizeak aplikazio lineal horren iraulia errepresentatzen du.
Antzeko matrizeak[aldatu | aldatu iturburu kodea]
Bi matrize antzekoak diran ikusteko, eta izanik:
- endomorfismo diagonalgarria bada, orduan: -ri elkartura dago eta diagonalgarria bada .
- matrizea diagonalgarria bada, orduan: eta matrizeak antzekoak dira eta diagonalgarria bada.
Erreferentziak[aldatu | aldatu iturburu kodea]
- ↑ Matrizeko zenbakiak biltzeko, parentesi zabalak erabili daitezke kortxeteen ordez.


![{\displaystyle A=[a_{i,j}]_{3\times 2}={\begin{bmatrix}1&2&3\\6&5&4\end{bmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e07b9939a95543a4bea25bc6d7f747df2dad5b4)





































