Koadrika
Geometrian, koadrika, edo gainazal koadrika, bigarren mailako ekuazio batek eragiten duen gainazala da, hots, itxura honetakoa:
non P bigarren mailako polinomio bat den koordenatuetan.
Zehazten ez bada, ohiko espazio tridimentsional errealeko gainazala da, koordenatu-sistema ortogonal eta unitario, eta koordenatuak hauek dira: x, y, z.

Historia[aldatu | aldatu iturburu kodea]
Antzineko Greziako matematikariak izan ziren lehenengoak koadrikak ikasten, konoa (koadrika bat) eta bere ebakidurak, plano bidimentsionaleko koadrikak direnak, baina, ez zuten erabili ekuaziorik.
Definizio aljebraikoa[aldatu | aldatu iturburu kodea]
koadrika edo gainazal koadrika bat, hipergainazal D-dimentsional bat da, espazio-aldagai (koordenatuak) dituen bigarren mailako ekuazio batek adierazita. Koordenatu horiek badira, orduan espazio horretako ohiko koadrikak ekuazio aljebraiko hau dauka:
non Q (D) dimentsioko matrize karratu bat den , P (D) dimentsioko bektore bat eta R konstante bat. Q, P eta R, orokorrean, errealak edo konplexuak izan arren, koadrika bat defini daiteke edozein eraztunaren gainean.
Ekuazio kartesiarra[aldatu | aldatu iturburu kodea]
Gainazal koadrikaren ekuazio kartesiarra honela da:
non A-tik J-rako koefizienteak errealak diren, eta A,B,C,D,E,F ez dira guztiak nuluak.
Ekuazio normalizatua[aldatu | aldatu iturburu kodea]
Koadrika tridimentsional (D = 3) baten ekuazio normalizatua, espazio tridimentsionaleko (0, 0, 0) jatorrian zentratua, hau da:
Koadrika motak[aldatu | aldatu iturburu kodea]
| Gainazal koadrika propioak | ||
|---|---|---|
| Elipsoidea | 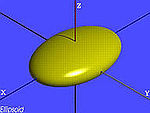
| |
| Esferoidea (elipsoidearen kasu berezia) | ||
| Esfera (esferoidearen kasu berezia) | ||
| Paraboloide eliptikoa | 
| |
| Paraboloide zirkularra (paraboloide eliptikoaren kasu berezia) | ||
| paraboloide hiperbolikoa | 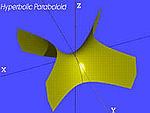
| |
| Hiperboloide azalbakarra edo hiperbolikoa | 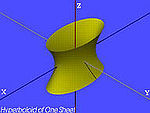
| |
| Azal biko hiperboloidea edo hiperboloide eliptikoa | 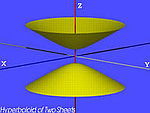
| |
| Gainazal koadrika endekatuak | ||
| Kono eliptikoa | 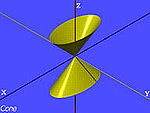
| |
| Kono Zirkularra (kono eliptikoaren kasu berezia) | ||
| Zilindro eliptikoa | 
| |
| Zilindro zirkularra (zilindro eliptikoaren kasu berezia) | ||
| Zilindro hiperbolikoa | 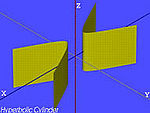
| |
| Zilindro parabolikoa | 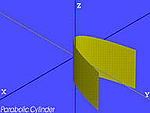
| |
Ikus, gainera[aldatu | aldatu iturburu kodea]
Kanpo estekak[aldatu | aldatu iturburu kodea]
- (Gaztelaniaz) Koadrikak, wmatem.eis.uva.es




















