Izar-poligono
| |||||||||
| Schläfli-sinboloa 2<2q<p zkh(p,q)=1 |
{p/q} | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Erpinak eta aldeak | p | ||||||||
| CDD |     
| ||||||||
| Simetria-taldea | Dp | ||||||||
| Poligono duala | Autoduala | ||||||||
| Barne-angelua | [1] | ||||||||
Izar-poligonoa izar itxurako poligono ahurra da. Gaur arte, erregularrak baino ez dira sakon aztertu; orokorrean, izar-poligonoak oraindik ez dituzte formalki definitu. Ez ditugu nahasi behar izar-multzoekin.
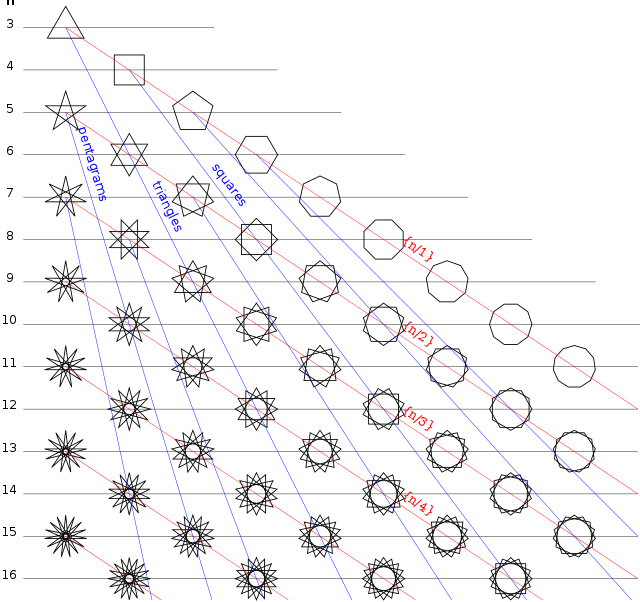
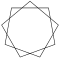
Izar-poligono erregularrak[aldatu | aldatu iturburu kodea]
Geometrian, "izar-poligono erregularra" elkar ebakitzen duten aldeak dituen poligono aldeberdin eta angeluberdina da, poligono ganbil baten erpinak ondoz ondokoak ez direnekin hainbestetik behin konektatuz sortua[2].
Adibideak[aldatu | aldatu iturburu kodea]
 Pentagrama |
 Hexagrama |
 Heptagrama |
 Oktograma |
 Eneagrama |
 Eneagrama |
 Dekagrama |
| ||||||
 {8/3} izar-poligono bat (oktograma) oktogono baten barruan eraikia |
.svg) |
Ikus, gainera[aldatu | aldatu iturburu kodea]
Erreferentziak eta oharrak[aldatu | aldatu iturburu kodea]
- ↑ Kappraff, Jay. (2002). Beyond measure: a guided tour through nature, myth, and number. World Scientific, 258 or. ISBN 978-981-02-4702-7.
- ↑ Elhuyar Zientzia eta Teknologiaren Hiztegi Entziklopedikoa. Izar-poligonoa. .
Kanpo estekak[aldatu | aldatu iturburu kodea]
- (Ingelesez) Weisstein, Eric W.: "Izar-poligono" MathWorld-en.
- {en} Star Polygons – java applet
| Autoritate kontrola |
|
|---|
Datuak: Q836708
Multimedia: Star polygons
| |||||||||||||||||||
