Triangelu: berrikuspenen arteko aldeak
t Robota: Testu aldaketa automatikoa (-{{HezkuntzaPrograma}} +{{HezkuntzaPrograma|Matematika}}) |
t Robota: Aldaketa kosmetikoak |
||
| 77. lerroa: | 77. lerroa: | ||
Hiruki baten [[azalera (poligono)|azalera]] zenbait eratara kalkula daiteke: |
Hiruki baten [[azalera (poligono)|azalera]] zenbait eratara kalkula daiteke: |
||
* hirukiaren altueraren bitartez, |
* hirukiaren altueraren bitartez, |
||
* hirukiko aldeen luzeraren bitartez, |
* hirukiko aldeen luzeraren bitartez, |
||
* erpinen [[koordenatu sistema|koordenatuen]] bitartez. |
* erpinen [[koordenatu sistema|koordenatuen]] bitartez. |
||
| 83. lerroa: | 83. lerroa: | ||
=== Azalera altueraren bitartez === |
=== Azalera altueraren bitartez === |
||
[[Fitxategi:Triangle aire.png| |
[[Fitxategi:Triangle aire.png|eskuinera|frame|Altuera marraztuz hirukia bi hiruki zuzenetan zatitzen da. Eta hiruki zuzen hauetako bakoitza laukizuzen baten erdia da.]] |
||
Hiruki baten altuera alde batetik aurkako erpinerainoko elkarzuta da. Altuera marrazten denean, hirukia bi hiruki zuzenetan zatitzen da. |
Hiruki baten altuera alde batetik aurkako erpinerainoko elkarzuta da. Altuera marrazten denean, hirukia bi hiruki zuzenetan zatitzen da. |
||
Hiruki zuzen baten azalera berehalakoa da: [[angelu zuzen]]a osatzen duten bi aldeen luzerak biderkatzen dira eta emaitza zati 2 egiten da, hiruki zuzena berak osatzen duen [[laukizuzen]]aren erdia baita. |
Hiruki zuzen baten azalera berehalakoa da: [[angelu zuzen]]a osatzen duten bi aldeen luzerak biderkatzen dira eta emaitza zati 2 egiten da, hiruki zuzena berak osatzen duen [[laukizuzen]]aren erdia baita. |
||
Hiruki bat osatzen duten bi hiruki zuzenen azaleren [[batuketa]] eginez, argi dago honela kalkulatzen dela hiruki baten azalera, ''a'' alde bat eta ''h'' alde horri dagokion altueraren luzera izanik: |
Hiruki bat osatzen duten bi hiruki zuzenen azaleren [[batuketa]] eginez, argi dago honela kalkulatzen dela hiruki baten azalera, ''a'' alde bat eta ''h'' alde horri dagokion altueraren luzera izanik: |
||
| 101. lerroa: | 101. lerroa: | ||
non ''p'' triangeluaren ''erdiperimetroa'' den: |
non ''p'' triangeluaren ''erdiperimetroa'' den: |
||
:<math>p=\dfrac{a+b+c}{2}.</math> |
:<math>p=\dfrac{a+b+c}{2}.</math> |
||
=== Erpinen koordenatuen bitartez === |
=== Erpinen koordenatuen bitartez === |
||
| 107. lerroa: | 107. lerroa: | ||
Erpinak bi dimentsioko plano batean badaude, ''A'', ''B'' eta ''C'' erpinen koordenatuak <math>A(x_A, y_A)</math>, <math>B(x_B, y_B)</math> eta <math>C(x_C, y_C)</math> izanik, [[determinante]]a erabiliz, hau izango da hirukiaren azalera: |
Erpinak bi dimentsioko plano batean badaude, ''A'', ''B'' eta ''C'' erpinen koordenatuak <math>A(x_A, y_A)</math>, <math>B(x_B, y_B)</math> eta <math>C(x_C, y_C)</math> izanik, [[determinante]]a erabiliz, hau izango da hirukiaren azalera: |
||
<math>S=\dfrac{1}{2} \left| \det\begin{pmatrix}x_A & x_B & x_C \\ y_A & y_B & y_C \\ 1 & 1 & 1\end{pmatrix} \right| = \dfrac{1}{2} \big| x_A y_C - x_A y_B + x_B y_A - x_B y_C + x_C y_B - x_C y_A \big|. </math> |
<math>S=\dfrac{1}{2} \left| \det\begin{pmatrix}x_A & x_B & x_C \\ y_A & y_B & y_C \\ 1 & 1 & 1\end{pmatrix} \right| = \dfrac{1}{2} \big| x_A y_C - x_A y_B + x_B y_A - x_B y_C + x_C y_B - x_C y_A \big|. </math> |
||
Hiru dimentsiotan, ''ABC'' hirukiaren erpinen koordenatuak <math>A = (x_A, y_A, z_A)</math>, <math>B = (x_B, y_B, z_B)</math> eta <math>C = (x_C, y_C, z_C)</math> izanik, honela kalkulatzen da hirukiaren azalera: |
Hiru dimentsiotan, ''ABC'' hirukiaren erpinen koordenatuak <math>A = (x_A, y_A, z_A)</math>, <math>B = (x_B, y_B, z_B)</math> eta <math>C = (x_C, y_C, z_C)</math> izanik, honela kalkulatzen da hirukiaren azalera: |
||
13:56, 22 otsaila 2019ko berrikusketa
| Hirukia | |
|---|---|
 Hiruki edo triangelu bat | |
| Aldeak | 3 |
| Schläfli sinboloa | {3} (aldeberdina) |
| Azalera | hainbat metodo |
| Barne-angelua | ° (aldeberdina) |
Geometrian, hirukia hiru alde eta hiru erpin dituen poligono bat da. Triangelu hitza ere erabiltzen da hirukia izendatzeko, poligonoaren barrutia osatzen duten hiru angeluak direla eta. Geometriako funtsezko irudietako bat da eta antzinatik ebazkizun eta teorema anitz asmatu da berari buruz. Aplikazio zabalak ditu: trigonometria hirukian oinarritzen den matematika-alorra da, besteak beste geodesian erabiltzen dena.
Notazioa
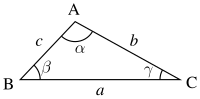
Beste irudi geometrikoetan bezala, triangeluaren erpinak letra maiuskulaz izendatu ohi dira: A, B eta C edo bestelako letra erabiliz. Horrela, triangelua bere erpinak aipatuz izen daiteke: ABC. Zuzenkiak bezalaxe, triangeluko aldeek bere muturrak aipatuz izendatzen dira: AB (edo BA) aldea, BC aldea, AC aldea. Alde hauen luzera adierazi nahi denean, letra minuskulak erabiltzen dira: a aldea A erpinaren aurkako BC aldearen luzera izango da.
Propietate geometrikoak
- A, B eta C plano bateko hiru puntu ez-lerrokatuk hiruki bat osatzen dute. Hiru dimentsioko espazioko hiru puntu ez lerrokatuz ere hiruki bat sortzen dute.
- Diagonalik ez duen poligono bakarra da.
- Poligono oro hirukietan zati daitezke, ondokoak ez diren erpinak lotuz. n aldeko poligono bat zatitzeko n-2 hiruki behar dira gutxienez (adibidez, karratua (4 alde) 2 hirukitan zatitzen da diagonal bat marraztuz).
Aldeen arteko erlazioa
Hiruki batean alde bakoitzaren luzera beste bi aldeen luzeren batura baino txikiagoa da:
Angeluen batura
Hiruki bateko barneko hiru angeluen neurrien batura 180º da.
Hiruki motak
Aldeei buruz
- Hiruki aldekidea (edo aldeberdina): hiruki bat non alde guztiek luzera bera duten eta angelu guztiek 60º duten.
- Hiruki isoszelea: hiruki bat non bi alde berdinak diren.
- Hiruki eskalenoa: hiruki bat non hiru aldeak desberdinak diren.
 |
 |
 |
| Aldekidea | Isoszelea | Eskalenoa |
Angeluei buruz
Angeluei buruz hiru mota bereizten dira:
- Hiruki zuzena: bere angelurik handienak 90º dituen hirukia da.
- Hiruki kamutsa: bere angelurik handienak 90º baino gehiago dituen hirukia da.
- Hiruki zorrotza: bere angelurik handienak 90º baino gutxiago dituen hirukia da.
 |
 |
 |
| Zuzena | Kamutsa | Zorrotza |
Hiruki baten azalera
Hiruki baten azalera zenbait eratara kalkula daiteke:
- hirukiaren altueraren bitartez,
- hirukiko aldeen luzeraren bitartez,
- erpinen koordenatuen bitartez.
Azalera altueraren bitartez

Hiruki baten altuera alde batetik aurkako erpinerainoko elkarzuta da. Altuera marrazten denean, hirukia bi hiruki zuzenetan zatitzen da.
Hiruki zuzen baten azalera berehalakoa da: angelu zuzena osatzen duten bi aldeen luzerak biderkatzen dira eta emaitza zati 2 egiten da, hiruki zuzena berak osatzen duen laukizuzenaren erdia baita.
Hiruki bat osatzen duten bi hiruki zuzenen azaleren batuketa eginez, argi dago honela kalkulatzen dela hiruki baten azalera, a alde bat eta h alde horri dagokion altueraren luzera izanik:
Aldeen luzeraren bitartez
a, b, c hirukiko aldeen luzerak izanik, honela kalkula daiteke hiruki baten azalera, Heronen formulari esker:
non p triangeluaren erdiperimetroa den:
Erpinen koordenatuen bitartez
Erpinak bi dimentsioko plano batean badaude, A, B eta C erpinen koordenatuak , eta izanik, determinantea erabiliz, hau izango da hirukiaren azalera:
Hiru dimentsiotan, ABC hirukiaren erpinen koordenatuak , eta izanik, honela kalkulatzen da hirukiaren azalera:
Hirukiaren zuzenki eta puntu nabariak
Erdikariak eta intzentroa

Hiruki bateko erdikariak bertako hiru barne-angeluen erdikariak dira. Hiruki bateko erdikariek bat egiten dute puntu batean, intzentro izenekoa. Intzentroa hirukian inskribatutako zirkunferentziaren erdiko puntua da.
Altuerak eta ortozentroa

Triangelu batean erpinetik pasatzen diren eta aurkako aldearekiko elkarzutak diren hiru zuzenei altuerak deritze. Altueraren eta aurkako aldearen ebaki-puntuari oina deritzo.
Hiru altuerak elkartzen diren puntu bakarrari H, triangeluaren ortozentroa, deitzen zaio.
Ikus, gainera
| Wikimedia Commonsen badira fitxategi gehiago, gai hau dutenak: Triangelu |














