Erlazio bitar
Matematikan, erlazio bitar bat eta multzoen elementuen artean definitutako matematika-erlazio bat da.
eta multzoen arteko erlazio bat propietatea betetzen duten bikote ordenaturen bidez adierazi ahal da, biderkadura cartesiarraren bikote ordenatuen azpimultzo batekoak. Notazio matematikoa erabiliz
egiazkoa
idatz daitekeena eta mintzatuz
' erlazio bitarra haietan propietatea betetzen den multzoaren elementuak multzoaren elementuekin lotzen dituzten bikote ordenatuen multzoa da'
adierazi.
Notazio matematiko ohikoenetan eta elementuen arteko erlazio bitarra hurrengo eratan adierazten da:
- edo edo
edo baita ere
- edo.
poloniar notazioa edo alderantzizko poloniar notazioa erabiltzen badira.
Adibidea
[aldatu | aldatu iturburu kodea]- zenbaki errealen multzoa emanda, planoko abzisen eta ordenatuen arteko erlazio bitar bat definitu ahal dugu, funtzio koadratikoa betetzen duten puntuak aukeratuz.
Notazio matematikoaz adierazten dena.
Erlazio bitarren taxonomia, sailkapen orokorra
[aldatu | aldatu iturburu kodea]Erlazio bitarren taxonomia erakusteko grafikoan, definizio orokorragoetatik espezifikoagoetara joateko jarrai gezien noranzkoa.

Erlazio bitarren garrantzia matematikan, multzoren zenbakidun eta ez zenbakidun elementuen arteko elkartze asko eta asko sarritan binaka egitetik dator; eta hori elementuak bai multzo berekoak direnean eta baita ere multzo ezberdinekoak direnean.
Goiko eskeman egitura aljebraiko edo erlazio bitarren azpimota batzuk agertzen dira. Eskema hori lagungarri izango dugu aurrerago erlazio mota horiek aztertzerakoan.
Lehenengo eta behin erlazio homogeneo eta heterogeneoak bereizi behar dira; lehenengoetan erlazio bitarrak multzo bereko elementuen artekoak dira eta, horren ondorioz, multzo horren barne egitura bati lotuta daude; bigarrenetan erlazioak bi multzo ezberdinen elementuen artekoak dira eta kalkulu-eragiketa edo funtzioei lotuta izaten ohi dira. Erlazio homogeneo bat erlazio heterogeneoen moduan ere sailkatu ahal da, baina ez alderantziz.
Erlazio homogeneoak
[aldatu | aldatu iturburu kodea]Multzo biren arteko erlazio bitar bat homogeneoa da multzo biak multzo bera direnean:
A eta B multzoak multzo bera direnez,
idatzi ohi da, edo
Erlazio heterogeneoak
[aldatu | aldatu iturburu kodea]A eta B multzo biren arteko erlazioa heterogeneoa da A eta B multzoak multzo bera ez direnean:
multzoari erlazioaren abiaburu-multzoa deitzen zaio eta multzoari erlazioaren helburu-multzoa. Erlazio batean partaideak diren multzoko elementuek erlazioaren aurreirudi-multzoa edo erlazioaren izate-eremua (ingelesez domain) osatzen dute eta multzokoek erlazioaren irudi-multzoa[1] (ingelesez range).
Aurrez ikusi beharreko kontzeptuak
[aldatu | aldatu iturburu kodea]Erlazio bitarrak aztertu baino lehen badaude ezagutzea komeni den kontzeptu batzuk; garrantzitsuenak hurrengoak dira:
Bikote ordenatuak
[aldatu | aldatu iturburu kodea]bikote ordenatu bat lehenengo elementu bat eta bigarren elementu bat dituen objektu matematikoen bikote bat da. Lehenengo elementua a eta bigarren elementua b dituen bikote ordenatua irudikatzeko (a,b) idazten da.
(a,b) bikote ordenatua ez da {a,b} idazten den a eta b elementuez osatuta dagoen multzoa. Multzo bat bera osatzen duten elementuez baino ez dago definitua, bikote ordenatu bat definitzerakoan, aldiz, elementuen ordena ere kontuan hartu behar da. Adibidez, {0, 1} eta {1, 0} multzoak multzo bera dira baina (0, 1) eta (1, 0) bikote ordenatuak bi bikote ezberdinak dira.
Bikote ordenatuak 2-tuplak edo 2 dimentsioko bektoreak ere izendatzen dira. Ordenatuta dauden objekturen bilduma finituaren nozioa objektu pare bat baino gehiagorako zabaldu ahal da eta n-koteren kontzeptua sortu.
(a, b) bikote ordenatu baten osagaiak hurrengoak dira:
- Lehenengo multzoari dagokion a lehenengo osagaia
- Bigarren multzoari dagokion b bigarren osagaia
Biderkadura cartesiarra
[aldatu | aldatu iturburu kodea]A eta B multzoen AxB biderkadura cartesiarra lehenengo osagaia A multzoko elementuez eta bigarrena B multzoko elementuez osatutako bikote ordenatu guztien multzoa da.
Eta notazio matematikoan
idazten da.
Hurrengo bi multzoak baditugu:
AxB biderkadura cartesiarra lortzeko A multzoaren elementuak taula baten ardatz horizontalean eta B multzoarenak ardatz bertikalean jartzen dira eta gurutzaketa gelaxketan gagozkien bikote ordenatuak; kontuan izanda bikote ordenatuetan lehenengo tokian ardatz horizontaleko A multzoaren elementuak jarri behar direla eta bigarren tokian ardatz bertikaleko B multzoarenak.
Bikote ordenatuen multzoaren elementuak hurrengoak lirateke:
Erlazio bitarrak: biderkadura cartesiarraren azpimultzoak
[aldatu | aldatu iturburu kodea]AxB biderkadura cartesiarra ikusita, erlazio bitar bat, adibidez baino txikiagoa erlazioa, biderkadura cartesiar horren azpimultzo baten bidez adierazi ahal da.
- Oharra: a>b adierazpen matematikoaren esangura hurrengoa da:
- ingelesez 'a (is) greater than b', frantsesez 'a (est) plus grand que b', espainieraz 'a (es) mayor que b'
- eta euskaraz 'a handiagoa (da) b baino' edo, gauza bera dena, 'a baino txikiagoa (da) b'
- eta irakurtzen denean, aditza ezabatuz, hurrengoa esan ohi dute matematikariek:
- ingelesez 'a greater than b', frantsesez 'a plus grand que b', espainieraz 'a mayor que b'
- eta euskaraz, jende arruntarentzat ulergarria izateko inguruko hizkuntzen formari hurbilegi jarraituz, 'a handiago b'
- baina hau jende arruntarentzat ia ulertu ezina da, konparaketa nolakoa den jakiteko funtsezkoa den bainoa ere, ezabatzen delako;
- hori dela eta, jende arruntarentzat ulergarriagoa gerta dadin
- artikulu honetan a>b adierazpena 'a baino txikiagoa b' irakurriko da.
eta parte hartzen duten bikote ordenatu guztiak banan banan idatziz:
Erlazio bitarra definitzen duten bikote ordenatuak multzoen biderkadura cartesiarraren azpimultzo bat direla.[2]
|
Hori dela eta, multzo biren artean izan litezkeen erlazio bitarren kopurua estimatu ahal da.
badira
A eta B multzoen artean izan litezkeen erlazio bitarren kopurua hurrengoa da:
Multzoren bat infinitua izanez gero aurreko kopurua zenbaki transfinitua legez hartu behar da.
Erlazio bitar homogeneoak
[aldatu | aldatu iturburu kodea]Aurrerago esan den legez, erlazio bitar homogeneo bat multzo bakar baten elementuen artekoa da; multzo hori A multzoa bada notazio matematikoz honela adierazten da:

Erlazio bitarrak multzo bakar baten elementuen artekoak direnean, erlazio horiek multzoak modu ezberdinetan egituratu ahal dituzte, egitura bat ematen diete multzoei eta multzoak sortutako egitura horien arabera sailka daitezke. Eredu baten bidez ikusiko dugu nola irudikatu horrelako erlazioak:
Alboko irudian geziez irudikatzen den multzoaren elementuen arteko erlazioan multzo bakar bat dagoela eta erlazionatuta duden elementu guztiak haren barnekoak direla ikusten da.
Erlazio berbera erlazionatuta dauden elementuen eralzio zerrenda batez irudikatu ahal da:
edo bikote ordenaturen multzo baten bidez:
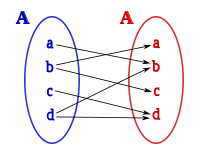
Erlazio bitar homogeneo bat Atik Arako korrespondentzia bat bezala ere, irudikatu ahal da:
A multzoa abiaburu-multzo legez hartuz eta, baita ere, helburu-multzo bezala.
Kasu honen erlazio bitarra aztertzeko erlazio bitar heterogeneoak aztertzerakoan erabiltzen diren irizpideak erabili ahal dira, eta haien arabera sailkatu erlazioa.
Erlazio bitar baten irudikapena biderkadura cartesiarraren azpimultzo batez:
| d | (a, d) | (b, d) | (c, d) | (d, d) |
| c | (a, c) | (b, c) | (c, c) | (d, c) |
| b | (a, b) | (b, b) | (c, b) | (d, b) |
| a | (a, a) | (b, a) | (c, a) | (d, a) |
| A×A | a | b | c | d |
Alboko taulan biderkadura cartesiarraren bikote ordenatu guztiak agertzen dira; ereduaren erlazioa irudikatzeko balio dutenak letra lodiz nabarmenduta daudela.
Beraz, hurrengoa da erlazioa irudikatzeko erabili ahal den biderkadura cartesiarraren azpimultzoa:
Kontuan hartu ardatz horizontalean abiaburu-multzoa irudikatzen dela eta bertikalean helburu-multzoa.
Erlazio bitar homogeneoen propietateak
[aldatu | aldatu iturburu kodea]Bera osatzen duten bikote ordenatuen arabera, erlazio bitar batek propietate ezberdin batzuk izan ditzake. Ikus ditzagun euretariko batzuk:
Propietate erreflexiboa
[aldatu | aldatu iturburu kodea]multzoaren elementuen arteko erlazio bitar homogeneo batek propietate erreflexiboa du multzoaren elementu guztiak euren buruekin erlazionatuta daudenean.
multzoaren elementu guztientzako biderkadura cartesiarraren bikote ordenatua erlazio bitarrarena da.
Kontuan izan multzoaren elementu guztiak egon behar direla erlazionatuta euren buruekin, euretariko batzuk ez badaude erlazionatuta euren buruekin erlazioa erlazio ez-erreflexiboa dela esaten da.
Goiko adierazpen matematikoaren baliokidea da hurrengoa:
Ez dago multzoaren elementurik erlazio bitarrean bikote ordenatua ez duenik.
Propietate irreflexiboa
[aldatu | aldatu iturburu kodea]Erlazio bitar batek propietate irreflexiboa du ez dagonean berberarekin erlazionatuta dagoen ezein elementurik:
Propietate honi propietate antierreflexiboa ere, esaten zaio batzuetan, eta beste era honetara ere, irudikatu ahal da notazio matematikoaz:
Ez dago berberarekin erlazionatuta dagoen multzoaren ezein elementurik.
Propietate simetrikoa
[aldatu | aldatu iturburu kodea]Erlazio bitar batek propietate simetrikoa du bikote ordenatu bat erlaziokoa izateak halabeharrez bikote ordenatua ere, erlaziokoa izatera behartzen duenean:
Gorago esandakoa kontuan izanda, bikote ordenatua erlazioarena ez bada bikotea ere, ezin da izan erlazioarena. Hori argi ikusten da goiko adierazpen matematikoaren baliokidea den hurrengo adierazpenean:
Ezin da egon ko ezein bikote ordenaturik bikote ordenatua ere koa ez bada.
Propietate antisimetrikoa
[aldatu | aldatu iturburu kodea]Erlazio bitar batek propietate antisimetrikoa du eta bikote ordenatuak aldi berean erlaziokoak izateak izatera behartzen duenean, hau da eta elementuak elementu berbera izatera behartzen duenean:
Beste era batera esanda, ez daude lehengoa bigarrenarekin eta aldi berean bigarrena lehenengoarekin erlazionatuta dauden eta elementu ezberdin bi:
Adibidez, (baino txikiago edo berdin) erlazioa antisimetrikoa da, eta baita (baino txikiago) erlazioa, baina bigarren kasu honetan definizioaren baldintza inoiz betetzen ez delako, hau da inoiz ez delako egia.
Propietate asimetrikoa
[aldatu | aldatu iturburu kodea]Erlazio bitar batek propietate asimetrikoa du eta bikote ordenatuak ezin direnean aldi berean erlaziokoak izan.
Erlazio bitar batek bakarrik du propietate asimetrikoa aldi berean propietate antisimetrikoa eta irreflexiboa dituenean.[3] Esate baterako, (baino txikiago) erlazioa asimetrikoa da, baina (baino txikiago edo berdin) erlazioa ez.
Propietate iragankorra
[aldatu | aldatu iturburu kodea]Erlazio bitar batek propietate iragankorra du multzoaren elementu bat elementuarekin eta elementua elementu batekin erlazionatuak egoteak elementua halabeharrez elementuarekin erlazionatuta egotera behartzen duenean:
Osotasun-propietatea
[aldatu | aldatu iturburu kodea]Erlazio bitar batek osotasun propietatea du eta, beraz, erlazio osoa da elementu guztiak euren artean erlazionatuta daudenean; hau da multzoaren eta edozein elementu beti daudenean erlazionatuta lehenengoa bigarrenarekin edo/eta bigarrena lehenengoarekin:
Erlazio ondo sortuak
[aldatu | aldatu iturburu kodea]multzo baten elementuen arteko erlazioa erlazio ondo sortua da multzoaren azpimultzo guztietan ez den azpimultzoaren edozein elementua bikotea erlazioarena ez izatea egiten duen elementua badago.
Hau da multzoaren azpimultzo guztietan azpimultzo horien elementu txikiena den elementu bat dago.
Erlazio bitar homogeneoen motak
[aldatu | aldatu iturburu kodea]Erlazio bitar homogeneoek izan ditzaketen propietateen arabera sailka daitezke; sailkapena egiteko propietate bakar bat kontuan hatuz gero hurrengo motak dira gehien erabilitakoak:
| Erlazio simetrikoa | |
| Erlazio antisimetrikoa | |
| Erlazio asimetrikoa | |
| Erlazio erreflexiboa | |
| Erlazio irreflexiboa | |
| Erlazio iragankorra | |
| Erlazio iragangaitza | |
| Erlazio zirkularra | |
| Erlazio osoa |
Propietate bat baino gehiago kontuan hartuz gero sailkapen zehatzagoa egin daiteke, beste mota batzuk ere erabiliz.
Jarraian sailkapen zabalagoaren edo zehatzagoaren nahiko interesgarriak diren erlazio mota batzuei buruzko informazio gehigarria a agertzen da:
Erlazio erreflexiboak
[aldatu | aldatu iturburu kodea]Propietate erreflexiboa duten erlazioei erlazio erreflexiboak deitzen zaie eta beste erlazio mota konplexuago batzuk aztertzeko abiaburu dira. Kontuan izan erlazio bitar ez-erreflexiboak eta irreflexiboak oso kasu berezietan agertzen direla eta, kasu arruntenetan daukaten garrantzi txikiagatik, gutxi ikertuak direla.
Erlazio erreflexiboen definizioa hurrengoa da:
multzoaren elementuen arteko erlazio bitar homogeneoa erlazio erreflexiboa da hurrengo propietatea duenean:
1.- Propietate erreflexiboa:
Propietate erreflexiboa duen erlazio baten eredurik argiena berdintza matematikoarena da; zenbaki multzo batean, zenbaki arrunten multzoan adibidez, edozein zenbakia berdina da berberarekin.

multzoaren elementuen arteko erlazioak propietate erreflexiboa du eta, beraz, erlazio erreflexiboa da, multzoaren elementu guztiak euren buruekin erlazionatuta daude eta.
Multzoaren elementu guztiak agertzen dira termino biak berdinak dituzten erlazioaren bikote ordenatuetan.

erlazioa koordenatu cartesiarren bidez ere, irudikatu ahal da.
Horretarako, ardatz horizontalean (abszisena) ezkerretik eskuinera abiaburu-multzoaren elementuak, ardatz bertikalean (ordenatuena) behetik gora helburu-multzoenak (kontuan izan erlazio homogeneotan abiaburu-multzoa eta helburu-multzoa multzo berbera direla) eta bikote ordenatu bat erlazioarena bada koordenatu biak gurutzatzen diren gelaxkan gurutze bat jarriz (kontuan izanda bikotearen lehengo terminoa ardatz horizontalari dagokiola eta bigarrena ardatz bertikalari).
Beheko ezker muturretik goiko eskuin muturrera doan diagonal nagusiko gelaxkak elementu biak berdinak dituzten bikote ordenatuei dagozkienak dira eta erlazioa erreflexiboa izan dadin diagonal horren gelaxka guztietan gurutze bat egon behar da.
Diagraman ikus dezakegu, ereduko erlazioa erreflexiboa dela.
Hiru irudikapen moduetako edozein (bikote ordenaturen zerrendakoa, gezi-diagramakoa edo koordenatu cartesiarrekoa) erabili ahal dugu erlazio bat erreflexiboa den ala ez ikusteko.
Erlazio ez-erreflexibo
[aldatu | aldatu iturburu kodea]Gehien aztertu diren erlazio bitar homogeneoak erlazio erreflexiboak dira, baina erlazio guztiak ez dira erreflexiboak. Propietate erreflexiboa ez duten erlazioak erlazio ez-erreflexibo deitzen dira eta erlazio hauen kasu berezia da inongo elementurik berberarekin erlazionatuta ez duten erlazio irreflexiborena. Orain arte ikusitakoaren arabera erlazio bitar homogeneoak beheko diagraman adierazten den moduan sailka daitezke.
Erlazio ez-erreflexiboen kasu berezia diren erlazio irreflexiboak honela definitzen dira:
multzoaren elementuen arteko erlazio bitar homogeneoa erlazio irreflexiboa da hurrengo propietatea duenean:
1.- Propietate irreflexiboa:
Gorago ikusi den moduan propietate irreflexiboa horrela ere irudikatu ahal da:
multzoan ez dago bere buruarekin erlazionatuta dagoen edozein elementurik.
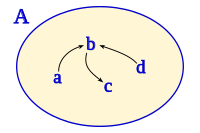
Alboan gezi-grafo baten bidez irudikatuta dagoen multzoaren elementuen arteko erlazioan
eta erlazioa irreflexiboa da.
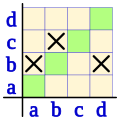
Erlazioa koordenatu cartesiarren bidez irudikatuz gero diagonal nagusian inolako gurutzerik agertzen ez dela ikusten da, erlazioa irreflexiboa izateko baldintza dena.
Propietate erreflexiboa eta irreflexiboa ezin dira batera bete; propietate erreflexiboa duen erlazio batean:
eta propietate irreflexiboa duen batean:
baina baldintza biak batera betetzea ezinezkoa da. Kontrako argudioa ez da zuzena, erlazio bitar bat batera izan daiteke EZ-erreflexiboa eta EZ-irreflexiboa. Ez-erreflexiboa den erlazio batean:
Eta ez-irreflexiboa den batean:
Eta baldintza horiek batera bete ahal dira, erlazioa aldi berean ez-erreflexiboa eta ez-irreflexiboa izanik.

Alboan gezi-grafo baten bidez irudikatuta dagoen multzoaren elementuen arteko erlazioan
Eta horren ondorioz, erlazioa ez da ez erreflexiboa ez irreflexiboa.

Koordenatu cartesiarrak erabiliz erlazioa irudikatzeko, diagonal nagusiko gelaxka guztietan gurutze bat ez dagoenez erlazioa erreflexiboa ez dela eta gelaxka horiek guztiak hutsik ez daudenez erlazioa irreflexiboa ez dela ikusten da; hau da erlazioa aldi berean da ez-erreflexiboa eta ez-irreflexiboa.
Laburbilduz, hiru motako erlazioak izan ditzakegu:
- Erlazio erreflexiboak
- Erlazio irreflexiboak
- Aldi berean ez-erreflexiboak eta ez-irreflexiboak diren erlazioak
Lotura erlazioak
[aldatu | aldatu iturburu kodea]Erlazio bitar homogeneo bat lotura-erlazioa da propietate erreflexiboa eta simetrikoa baditu:
multzoaren elementuen arteko erlazio bitar homogeneoa lotura-erlazioa da hurrengo propietateak dituenean:
1.- Propietate erreflexiboa:2.- Propietate simetrikoa:
Adibidez, zenbaki arrunten multzoa hartzen badugu eta bertan zenbaki biren arteko distantzia zenbaki horien arteko kenduraren balio absolutua dela definitu.
esaten badugu eta zenbaki arrunt bi hurbil daudela haien arteko distantzia balio finko bat baino handiagoa ez denean, hurbiltasun-erlazio bitarra hurrengoa da:
erlazio hori lotura-erlazioa da, propietate erreflexiboa:
eta simetrikoa:
dituelako. Hala ere hurbiltasun-erlazio bitarra ez da iragankorra
ez da betetzen eta.
Aldi berean eta -ren arteko distantzia eta eta -ren arteko distantzia baino handiagoak ez izateak ez du ziurtatzen eta -ren arteko distantzia baino handiagoak ez izatea. Distantzien araberako zenbakiren arteko lotura-erlazio honek ez du ezartzen euren artean inolako baliokidetasunik baina, euren arteko lotura bat bai.
Multzo aurreordenatuak
[aldatu | aldatu iturburu kodea]Erlazio bitar homogeneo batek multzo bati multzo aurreordenatuko egitura ematen dio propietate erreflexiboa eta iragankorra dituenean.
multzoaren elementuen arteko erlazio bitar homogeneoak multzoari multzo aurreordenatuko egitura ematen dio hurrengo propietateak dituenean:
1.- Propietate erreflexiboa:
2.- Propietate iragankorra:
Baliokidetasun-erlazioak
[aldatu | aldatu iturburu kodea]Erlazio bitar homogeneo bat baliokidetasun-erlazioa da propietate erreflexibo, simetriko eta iragankorra dituenean:[4]
multzoaren elementuen arteko erlazio bitar homogeneoa baliokidetasun-erlazioa da hurrengo propietateak dituenean:
1.- Propietate erreflexiboa:2.- Propietate simetrikoa:
3.- Propietate iragankorra:
Baliokidetasun-erlazio batek multzoa baliokidetasun-klasetan zatitzen du; haien elementu guztiak elkarrekin erlazionatuta dauden eta beste klase batzuetako elementuekin erlazionatuta ez dauden elementuz osatutako azpimultzotan. Azpimultzo horiek elkarrekin disjuntuak dira eta haien bilkura da. Ikus dezagun adibide bat:
Aritmetika modularrean zenbaki arrunten arteko kongruentzia-erlazioa definitzen da, zenbaki bi modulu batentzat kongruenteak direla definituz zenbaki biak modulu horrekin zatitzean hondar bera geratzen denean.
8 eta 17 kongruenteak dira 3 moduluarentzat, hiruz zatikatzean kasu bietan hondarra 2 delako.
Zenbaki arrunten n graduko modulu-kongruentzia baliokidetasun-erlazioa da, erreflexiboa:
simetrikoa:
eta iragankorra:
baita.
Multzo partzialki ordenatuak
[aldatu | aldatu iturburu kodea]Multzo bat erlazio bitar homogeneo batez partzialki ordenatua dago erlazio horrek propietate erreflexiboa, iragankorra eta antisimetrikoa baditu.
multzoaren elementuen arteko erlazio bitar homogeneoak multzoari multzo partzialki ordenatuko egitura ematen dio hurrengo propietateak dituenean:
1.- Propietate erreflexiboa:
2.- Propietate iragankorra:
3.- Propietate antisimetrikoa:
Ordena osoak
[aldatu | aldatu iturburu kodea]erlazio batek multzo batean ordena-osoa sortzen du erlazioa erreflexibo, iragankor, antisimetriko eta osoa bada:
multzoaren elementuen arteko erlazio bitar homogeneoak multzoari ordena osokoko egitura ematen dio hurrengo propietateak dituenean:
1.- Propietate erreflexiboa:
2.- Propietate iragankorra:
3.- Propietate antisimetrikoa:
4.- Osotasun-propietatea:
Esate baterako, zenbaki osoen multzoan baino handiagoa edo berdina erlazio bitarra ordena osoko erlazioa da, hurrengo baldintzak betetzen direlako
- (propietate erreflexiboa)
- (propietate iragankorra)
- (propietate antisimetrikoa)
- (osotasun-propietatea)
Multzo ondo ordenatuak
[aldatu | aldatu iturburu kodea]Ordena osoko multzo bat multzo ondo ordenatua da haren elementuen arteko erlazioa propietate erreflexibo, iragankor, antisimetriko eta osotasunekoaz hornitua izateaz gain, erlazio ondo sortua denean.
Haren elementuen artean erlazio bitarra duen multzo bat multzo ondo ordenatua da erlazioak hurrengo propietateak dituenean:1.- Propietate erreflexiboa:
2.- Propietate iragankorra:
3.- Propietate antisimetrikoa:
4.- Osotasun-propietatea:
5.- Erlazioa ondo sortua da:
Erlazio bitar heterogeneoak
[aldatu | aldatu iturburu kodea]
eta multzoen arteko erlazio bitar bat heterogeneo dela esaten da eta multzoak ezberdinak direnean:
Korrespondentzia (matematiko) ere, deitzen zaio.[5][6]
Eskuinaldeko irudia erlazio bitar heterogeneo baten gezi-diagrama da, bertan haien elementuek erlazionatuta dituzten bi multzoak agertzen dira, erlazionatuta dauden elementuak aurreirudietatik irudietara doazen geziez lotuta daudela. multzoan margo batzuekin hornitutako pintzelak agertzen dira eta multzoan margo horiekin margotutako aurpegiak, eta aurpegi bakoitza bera margotzeko erabili daitezkeen pintzelekin lotuta dago.
Baliteke margo bereko pintzelak edo aurpegiak egotea, baina multzoaren elementu desberdintzat hartu behar dira; pintzel edo aurpegi batzuk margo berekoak badira ezaugarri bera duten pintzel edo aurpegia ezberdinak dira.
Diagraman erlazioa definituta dagoen pintzelen abiaburu-multzoa ikus dezakegu:
Abiaburu-multzoko elementu guztiak ez daude erlazionatuta aurpegien multzoaren elementurekin. Erlazionatuta dauden elementuez osatuta dagoen multzoari aurreirudi-multzo deitzen zaio:
eta margotuta dauden aurpegien helburu-multzoa:
Erlazioan partaideak diren helburu-multzoko elementuez osatutako multzoari irudi-multzo deitzen zaio.
Erlazio bitarra hurrengo bikote ordenatuek osatzen dute:
- bezalako erlazio bitar homogeneo bat erlazio heterogeneo baten moduan ere aztertu ahal da, abiaburu-multzoa eta helburu-multzoa ezberdinak izango balira legez. Beraz, erlazio homogeneoak bi modutara azter daitezke.
Erlazio bitar heterogeneoen propietateak
[aldatu | aldatu iturburu kodea]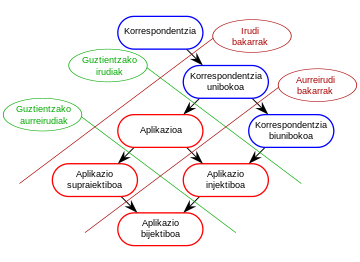
- erako erlazio bitar heterogeneo edo korrespondentzien azpimota batzuk aztertzeko daukaten garrantziagatik komeni da aurretik hurrengo propietateak (edo baldintzak) ikustea:
Irudien existentziaren baldintza
[aldatu | aldatu iturburu kodea]
Irudien existentziaren baldintza betetzen da multzoaren elementu guztiek multzoan irudi bat behintzat dutenean. Ez da nahikoa multzoan irudi batzuk egotea, beharrezkoa multzoaren elementu guztiek irudi bat gutxienez izatea:
Eskuineko irudian irudikatu den korrespondentzian baldintza betetzen da, multzoaren pintzel guztiek irudi bat gutxienez daukatelako aurpegien multzoan.
Aurreirudien existentziaren baldintza
[aldatu | aldatu iturburu kodea]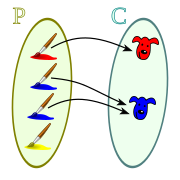
Aurreirudien existentziaren baldintza betetzen da multzoaren elementu guztiek multzoan aurreirudi bat behintzat dutenean. Ez da nahikoa multzoan aurreirudi batzuk egotea, beharrezkoa multzoaren elementu guztiek aurreirudi bat gutxienez izatea.:
Eskuineko irudian irudikatu den korrespondentzian baldintza betetzen da, multzoaren aurpegi guztiek aurreirudi bat gutxienez daukatelako pintzelen multzoan.
Irudi bakarreko baldintza
[aldatu | aldatu iturburu kodea]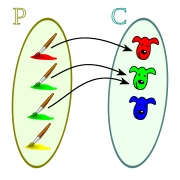
Irudi bakarreko baldintza betetzen da multzoan irudia duten multzoaren elementu guztiek irudi bakar bat dutenean. Baldintza ez da irudi bakar bat egotea, irudia duten aurreirudiek irudi bakar bat edukitzea baino:
Irudi bakarreko baldintzak irudia duten multzoaren elementuek irudi bakarra dutela ziurtatzen du, baina ez multzoaren elementu guztiek irudia dutenik.
Eskuineko irudian irudikatu den korrespondentzian baldintza betetzen da, irudia duten multzoaren pintzel guztiek irudi bakarra dutelako aurpegien multzoan.
Aurreirudi bakarreko baldintza
[aldatu | aldatu iturburu kodea]
Aurreirudi bakarreko baldintza betetzen da multzoan aurreirudia duten multzoaren elementu guztiek aurreirudi bakar bat dutenean. Baldintza ez da aurreirudi bakar bat egotea, aurreirudia duten irudiek aurreirudi bakar bat edukitzea baino:
Aurreirudi bakarreko baldintzak aurreirudia duten multzoaren elementuek aurreirudi bakarra dutela ziurtatzen du, baina ez multzoaren elementu guztiek aurreirudia dutenik.
Eskuineko irudian irudikatu den korrespondentzian baldintza betetzen da, aurreirudia duten multzoaren aurpegi guztiek aurreiirudi bakarra dutelako pintzelen multzoan.
Eredu-galeria
[aldatu | aldatu iturburu kodea]Elkarrengandik independenteak diren lau baldintza horien arabera agertu ahal diren kasuen eredu batzuk ikusiko ditugu.
Abiaburu-multzoak margo-tuturen multzoak izango dira, helburu-multzoak pintzelen multzoak; eta erlazioak margoak bat etortzean oinarrituta egongo dira.
Erlazio bitar heterogeneoen motak
[aldatu | aldatu iturburu kodea]
Erlazio bitar heterogeneoen artean hurrengo motak bereiz ditzakegu:
Korrespondentzia uníbokoak
[aldatu | aldatu iturburu kodea]Korrespondentzia bat unibokoa da irudi bakarreko baldintza betetzen denean:
erlazio bitar heterogeneoa korrespondentzia unibokoa da hurrengo baldintza betetzen bada:1.- Irudi bakarreko baldintza:
Baldintza hau beharrezkoa eta nahikoa da korrespondentzia unibokoa izan dadin.
Korrespondentzia biuníbokoak
[aldatu | aldatu iturburu kodea]Korrespondentzia bat biuníbokoa da (edo bana-banakoa) irudi bakarreko eta aurreirudi bakarreko baldintzak betetzen direnean:
erlazio bitar heterogeneoa korrespondentzia biunibokoa da hurrengo baldintzak betetzen badira:1.- Irudi bakarreko baldintza:
2.- Aurreirudi bakarreko baldintza:
Aplikazioak
[aldatu | aldatu iturburu kodea]eta multzoen arteko korrespondentzia bati aplikazioa deitzen zaio ren elementu guztiek irudi bakar bat badute irudi-multzoan,[7][8][6][9][10][11] hau da irudi bakarreko baldintza eta irudien existentziaren baldintza betetzen badira.
Aurreko lerro bietan agertzen den moduan irudikatuta dagoen erlazio bat aplikazio bat izan dadin multzoaren elementu guztiak multzoaren elementu bakar batekin egon behar dira erlazionatuta; eta notazioa matematikoa erabiliz honela adierazi ahal da:
- Abiaburu-multzoa eta helburu-multzoa zenbakidunak direnean aplikazioei aplikazio deitu ordez askotan funtzio izena ematen zaie.[12]
- Kopuru bi edo gehiagoren arteko erlazio edo korrespondentzia bati normalean funtzioa esaten zaio [13]
- Ingelesez aplikazio bati mapping deitzen zaio, normalean map-era laburbilduta.[14]
erlazio bitar heterogeneoa aplikazio bat da hurrengo baldintzak betetzen badira:1.- Irudi bakarreko baldintza:
2.- Irudien existentziaren baldintza:
Aplikazio injektiboak
[aldatu | aldatu iturburu kodea]Aplikazio bat injektiboa da aurreirudi bakarreko baldintza betetzen duen aplikazioa bada; beraz Aplikazio injektiboak irudi bakarreko, irudien existentziaren eta aurreirudi bakarreko baldintzak betetzen dituzten korrespondentziak dira.
erlazio bitar heterogeneo bat aplikazio injektiboa da hurrengo baldintzak betetzen badira:1.- Irudi bakarreko baldintza:
2.- Irudien existentziaren baldintza:
3.- Aurreirudi bakarreko baldintza:
Beraz, Aplikazio injektiboa aurreirudi bakarreko baldintza betetzen duen aplikazioa dela esan dezakegu; baina, baita ere, irudien existentziaren baldintza betetzen duen korrespondentzia biunibokoa.
Aplikazio supraiektiboak
[aldatu | aldatu iturburu kodea]Aplikazio bat supraiektiboa da aurreirudien existentziaren baldintza betetzen duen aplikazioa bada; beraz Aplikazio injektiboak irudi bakarreko, irudien existentziaren eta aurreirudien existentziaren baldintzak betetzen dituzten korrespondentziak dira.
erlazio bitar heterogeneo bat aplikazio supraiektiboa da hurrengo baldintzak betetzen badira:1.- Irudi bakarreko baldintza:
2.- irudien existentziaren baldintza:
3.- Aurreirudien existentziaren baldintza:
Aplikazio bijektiboak
[aldatu | aldatu iturburu kodea]Aplikazio bat bijektiboa da aldi berean aplikazio injektiboa eta supraiektiboa denean. Beraz, aplikazio bijektiboa irudi bakarreko, irudien existentziaren, aurreirudi bakarreko eta aurreirudien existentziaren baldintzak betetzen dituen korrespondentzia da.
eta multzoen arteko erlazio bitar heterogeneo bat aplikazio bijektiboa da, hurrengo baldintzak betetzen direnean:
1.- Irudi bakarreko baldintza:
2.- Irudien existentziaren baldintza:
3.- Aurreirudi bakarreko baldintza:
4.- Aurreirudien existentziaren baldintza:
Erreferentziak
[aldatu | aldatu iturburu kodea]- ↑ Zurutuza, Iñaki. (2000). Oinarrizko aljebra. Elhuyar ISBN 84-95338-18-1..
- ↑ ISBN 978-84-368-0174-3..
- ↑ (Ingelesez) Nievergelt, Yves. (2002). Foundations of Logic and Mathematics: Applications to Computer Science and Cryptography. Springer-Verlag, 158 or...
- ↑ (Gaztelaniaz) Gutiérrez Gómez, Andrés. (1981). Álgebra lineal. (1. argitaraldia) Ediciones Pirámide, S.A. ISBN 978-84-368-0174-3..
- ↑ (Gaztelaniaz) José Juan Carreño Carreño. (2008). (pdf) ÁLGEBRA Curso 2008/09. , 12 or..
- ↑ a b (Gaztelaniaz) Notas de álgebra. Universidad Politécnica de Valencia. Servicio de Publicaciones, 18 or. ISBN 978-84-9705-623-6..
- ↑ .
- ↑ (Gaztelaniaz) Mario López Gómez. (2005). (pdf) Algebra I. , 5 or..
- ↑ (Gaztelaniaz) Gregori Gregori, Valentín; Ferrando, J. C.. (2011). Matemática discreta. (8. argitaraldia) Editorial Reverté, S.A., 48 or. ISBN 978-84-291-5179-4..
- ↑ (Gaztelaniaz) Alegre Gil, Carmen. (1997). Problemas de matemática discreta. (1. argitaraldia) Universidad Politécnica de Valencia. Servicio de Publicaciones., 189 or. ISBN 978-84-7721-495-3..
- ↑ (Gaztelaniaz) Ayres, Frank. (1992). Álgebra moderna. (1. argitaraldia) McGraw-Hill ISBN 968-422-917-8..
- ↑ (Gaztelaniaz) Gutiérrez Gómez, Andrés. (1981). Álgebra lineal. Ediciones Pirámide, S.A., 131 or. ISBN 978-84-368-0174-3..
- ↑ (Gaztelaniaz) Alejandro Carreiras. Monografias.com: Ayuda Matemáticas ESO.. , 2. Funciones or..
- ↑ Txantiloi:Esisbn=84-276-1235-4 Maravall Casesnoves, Dario. (1982). Diccionario de matematicas modernas. Editorial nacional.
Bibliografia
[aldatu | aldatu iturburu kodea]liburuak[1] [2] [3] [4] [5] [6]
- ↑ (Gaztelaniaz) González Gómez, Antonia. (2009). Álgebra lineal. Fundación Conde del Valle de Salazar ISBN 978-84-96442-28-3..
- ↑ (Gaztelaniaz) Baquerizo Azofra, Clara. (2008). Matemática discreta y álgebra lineal. (1. argitaraldia) Martín Gómez, Emilia ISBN 978-84-612-3787-6..
- ↑ (Gaztelaniaz) Climent Coloma, Joan Josep. (2001). Álgebra. Teoría de conjuntos y estructuras algebraicas. (1. argitaraldia) Editorial Club Universitario ISBN 978-84-8454-081-6..
- ↑ (Gaztelaniaz) Gutiérrez Gómez, Andrés. (1981). Álgebra lineal. Ediciones Pirámide, S.A. ISBN 978-84-368-0174-3..
- ↑ (Gaztelaniaz) Losada Rodríguez, Ramón. (1978). Análisis matemático. Ediciones Pirámide, S.A. ISBN 978-84-368-0096-8..
- ↑ (Gaztelaniaz) Losada Rodríguez, Ramón. (1973). Conjuntos Álgebra Lineal. ISBN 978-84-400-6592-6..




















































































































































