Multzo

Matematikan, multzo bat objektu ezberdinen bilduma da.^[1]^[2]^[3] Elementu deritzen objektu hauek edozein eratakoak izan daitezke, besteak beste, zenbakiak, letrak, pertsonak eta koloreak. Elementu horiek multzo baten parte direla esaten da nolabait bertan definiturik baldin badaude.

Multzo bat hura osatzen duten elementu guztiek betetzen duten propietate baten bitartez definitu ohi da. Zenbaki arrunten kasuan, esate baterako, zenbaki lehen izatearen propietatea kontuan hartuz gero, multzoa honela adierazi ahal izango litzateke:

{P}=\{2,3,5,7,11,13\,...\}

edo

{P}=\{n\in \mathbb {N} \mid {\text{n zenbaki lehena}}\}

Adierazpena[aldatu | aldatu iturburu kodea]

Notazioa[aldatu | aldatu iturburu kodea]

Multzoak hizki larriz: A, B, X, M...
Multzoko elementuak hizki xehez: a, b, c, x...
Zenbaki arruntak ( $\mathbb {N}$ ) zenbaki osoen ( $\mathbb {Z}$ ) barne daude eta hauek zenbaki arrazionalen ( $\mathbb {Q}$ ) barne. Era berean zenbaki arrazionalak ( $\mathbb {Q}$ ) zenbaki errealen ( $\mathbb {R}$ ) barnean daude, eta azken hauen zenbaki konplexuen ( $\mathbb {C}$ ) barne.
x elementua A multzokoa dela adierazteko: $x\in A$ (x barne A). Edo ez dela adierazteko: $x\not \in A$

Notazio berezia duten multzo batzuk[aldatu | aldatu iturburu kodea]

$\emptyset$ : Multzo hutsa, elementurik ez duen multzoa. $\emptyset$ = { }
$\cup$ : Unibertsoa, testuinguru bateko elementu guztien multzoa.
$\mathbb {Z} =\{...,-1,0,1\,...\}$ zenbaki osoen multzoa.
$\mathbb {Z} ^{+}=\{1,2,3\,...\}$ zenbaki oso positiboen multzoa.
$\mathbb {N} =\{0,1,2\,...\}$ zenbaki arrunten multzoa.
$\mathbb {R}$ : zenbaki errealen multzoa.
$\mathbb {C} =\{x+yi|x,y\in \mathbb {R} \}$ zenbaki konplexuen multzoa.

Multzo bat definitzeko moduak[aldatu | aldatu iturburu kodea]

Hedaduraz: bere elementu guztiak zerrendatuz edo infinitu elementu dituzten multzoen kasuan hasierakoak aipatuz argi gera dadin nola jarraitu daitekeen zerrenda. Adibidez, zenbaki arrunt bikoitien multzoa $\{2,4,6,8,...\}$ adieraz daiteke.

Ezaupidez: multzoko elementuek betetzen duten popietatea, edo propietateak, emanez. Adibidez, zenbaki arrunt bikoitien multzoa $\{n\in \mathbb {N} :\exists k\in \mathbb {N} ,n=2k\}$ moduan adieraz daiteke.

Multzo batean elementuen ordena ez da kontuan hartzen, eta multzoko elementuak zehaztean ez ditugu errepikatuko.

Adibidez: {a,b}={b,a}={a,a,b,a,b}

Multzoen historia[aldatu | aldatu iturburu kodea]

Matematikan, multzoaren kontzeptua, objektu abstraktu gisa, ez zen hasi erabiltzen XIX.mendera arte, infinituaren nozioari buruzko zalantzak argitzen hasi ziren arte, hain zuzen. Bernard Bolzano eta Bernhard Riemannen lanek jadanik ikuspegi konjuntistari lotutako ideiak zituzten. Richard Dedekindek aljebrari egindako ekarpenak termino argi eta garbian ezarri ziren, zeinak matematika modernoan gaur gun ere oraindik nagusia diren, besteak beste, baliokidetasun erlazioak, partizioak eta homomorfismoak. Horretarako behar izan zituen multzoekin lotutako hipotesi eta eragiketak ere hark landu zituen.

Multzoen teoria diziplina independente gisa Georg Cantori egotzi ohi zaio. Izan ere, zenbaki multzoen inguruko ikerketekin hasi, eta multzo infinituen nahiz haien propietateen inguruko ikerketa garatu zuen. Dedekind eta Cantorren eragina XIX.mendearen amaieran hasi zen erabakigarria izaten, matematikaren "axiomatizazio" prozesuan. Prozesu horretan, objektu matematiko guztiak, hala nola zenbakiak eta funtzioak, multzoak oinarritzat hartuta eraiki ziren.

Oinarrizko kontzeptuak[aldatu | aldatu iturburu kodea]

Multzoko elementuak[aldatu | aldatu iturburu kodea]

a elementu A multzo baten baitan dagoela honela adierazten da: $a\in A$ eta "a A multzoaren baitan dago" esaten da. Elementu bat multzo baitan ez dagoela honela adierazten da, berriz: $x\notin A\,$ .

Barnekotasuna eta azpimultzoak[aldatu | aldatu iturburu kodea]

Multzoak bata bestearen barnean ere izan daitezke. Adibidez, {0} multzoa {0,1,2} multzoaren barnean dago edo {0} {0,1,2} multzoaren azpimultzo bat dela esaten da. Barnekotasun-erlazioa honela adierazten da : $A\subseteq B$ (A multzoa B multzoaren barnean)^[4].

Multzo teorian bada multzo berezi bat: multzo hutsa edo $\emptyset$ multzoa da. Multzo hutsak badu propietate jakingarri bat: multzo hutsa multzo guztien barnean dago, hau da, A multzo guztietarako hau betetzen da: $\emptyset \subseteq A$ . Multzo oro beraren azpimultzo da: $A\subseteq A$

Multzo baten kardinala[aldatu | aldatu iturburu kodea]

Multzo batek elementu-kopuruari multzoren kardinala deritzo.^[5] X multzoaren kardinala $|X|\,$ adierazten da. Adibidez, $|\{0,1,2\}|=3\,$ . Kardinala ere infinitua izan daiteke, $\mathbb {N}$ zenbaki arrunten multzoaren kasuan bezala. ^[6]Orduan multzoa infinitua dela esaten da. Kardinal infinituak batzuk besteak baino handiagoak izan daitezke; $\mathbb {R}$ zenbaki errealen kardinala zenbaki arruntena baino handiagoa da, adibidez.

Azpimultzoak[aldatu | aldatu iturburu kodea]

Definizioa:[aldatu | aldatu iturburu kodea]

A multzoa B multzoaren azpimultzo dela esango dugu (A parte B), $A\subseteq B$ , baldin $\forall x\in A\Longrightarrow x\in B$ .

Adibideak:

$\{1,3\}\subset \{1,2,3,4\}$

$\{1,2,3,4\}\subseteq \{1,2,3,4\}$

Venn diagramak[aldatu | aldatu iturburu kodea]

Multzoen arteko erlazioak adierazeko Venn diagramak erabiltzen dira. A multzoa izanik, $\emptyset \subseteq A$ , $A\subseteq \cup$ , $A\subseteq A$

Multzo berdinak[aldatu | aldatu iturburu kodea]

Bi multzo A eta B berdinak dira, A=B, baldin elementu berberak badituzte, hau da, $A\subseteq B\,\,eta\,\,B\subseteq A.$

Azpimultzo propioa[aldatu | aldatu iturburu kodea]

A multzoa eta B multzoaren azpimultzo propioa da baldin $A\subseteq B$ , hau da, $A\subseteq B\,\,eta\,\,A\neq B$ .

Potentzia-multzoa[aldatu | aldatu iturburu kodea]

A multzo baten azpimultzo guztiek osatzen duten multzoari potentzia-multzo deritzo, eta P(A), ℘(A) edo 2^A adierazten da. Adibidez, S = {x, y, z} izanik, bere azpimultzoak ∅, {x}, {y}, {z}, {x, y}, {x, z}, {y, z} eta {x, y, z} dira, eta potentzia-multzoa ℘(S) = {{x, y, z}, {x, y}, {x, z}, {y, z}, {x}, {y}, {z}, ∅}. Potentzia-multzoaren kardinala multzoarena baino handiagoa da beti. Multzo baten kardinala n izanez gero, bere potentzia-multzoaren kardinala 2ⁿ da. Multzoa infinitua baldin bada, bai zenbakarria bai zenbakaitza, potentzia-multzoa infinitu zenbakaitza izango da. Zenbaki arrunten potentzia-multzoa bijekzio bidez zenbaki errealen multzoarekin lotu daiteke, esaterako.

Partizioa[aldatu | aldatu iturburu kodea]

A multzoaren partizioa A-ren azpimultzo ez-hutsen familia bat da, non azpimultzo hauek elkarren artean disjuntuak diren eta guztien bildura A den.

\mathrm {P} =\{A_{i}:i\in I\}\,\,\,{\bigl (}I:indize\,\,multzoa{\bigr )}

${\bigl (}\forall i\in I{\bigr )}\,\,\emptyset \neq A_{i}\subseteq A$ azpimultzo ez-hutsak.
${\bigl (}\forall i,j\in I{\bigr )}\,\,A_{i}\neq A_{j}\Rightarrow A_{i}\,\cap \,A_{j}=\emptyset$ $\cap$ :(Disjuntua)
$\cup _{i\in I}\,A_{i}=A$ (Hainbat multzoren bildura).

$A_{i}$ : partizioaren klaseak.

Eragiketak[aldatu | aldatu iturburu kodea]

Bilketa[aldatu | aldatu iturburu kodea]

A eta B bi multzok osatzen duten bildura A-renak diren edota B-renak diren elementuek osatzen duten multzoa da, A ∪ B bezala adierazten dena.

$A\cup B=\{a\,/\,a\in A\,\mathrm {edo} \,a\in B\}$

Adibideak:

{1, 2} ∪ {1, 2} = {1, 2}.
{1, 2} ∪ {2, 3} = {1, 2, 3}.
{1, 2, 3} ∪ {3, 4, 5} = {1, 2, 3, 4, 5}.

Bilketa ez da bi multzotara mugatzen, edozein multzo kopurutan definitu baitaiteke. Hurrengo propietateak betetzen ditu:

A ∪ B = B ∪ A
A ∪ (B ∪ C) = (A ∪ B) ∪ C
A ⊆ A ∪ B
A ∪ A = A
A ∪ ∅ = A
Baldin eta soilik baldin A ∪ B = B, orduan A ⊆ B

Ebakidura[aldatu | aldatu iturburu kodea]

A eta B bi multzoren ebakidura aldi berean A-renak eta B-renak diren elementuek osatzen duten multzoa da, A ∩ B bezala adierazten dena.

$A\cap B=\{a\,/\,a\in A\,\mathrm {eta} \,a\in B\}$

Adibideak:

{1, 2} ∩ {1, 2} = {1, 2}.
{1, 2} ∩ {2, 3} = {2}.
{1, 2} ∩ {3, 4} = ∅.

Bilketan bezala, ebakidura edozein multzo kopurutan defini daiteke. Hurrengo propietateak betetzen dira

A ∩ B = B ∩ A
A ∩ (B ∩ C) = (A ∩ B) ∩ C
A ∩ B ⊆ A
A ∩ A = A
A ∩ ∅ = ∅
A ⊆ B baldin eta soilik baldin A ∩ B = A

Bi multzoren ebakidura multzo hutsa denean, hau da, ez bada existitzen elementurik aldi berean bi multzoetan dagoena, multzo horiek disjuntoak direla esaten da.

Gainera, bilketa eta ebakiduraren artean propietate distributiboa betetzen da:

A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

Multzo osagarria[aldatu | aldatu iturburu kodea]

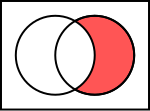
Bi multzoren arteko kenketa edo multzo osagarri erlatiboa B - A moduan idazten da (edota B ∖ A) eta A-renak ez diren B-ren elementuek osatutako multzoa da:

$B\setminus A=B-A=\{x\in B\,/\,x\notin A\}$

Adibideak:

{1, 2} \ {1, 2} = ∅.
{1, 2, 3, 4} \ {1, 3} = {2, 4}.

A, B eta C hiru multzoren artean hurrengo erlazioak betetzen dira:

C ∖ (A ∩ B) = (C ∖ A)∪(C ∖ B)
C ∖ (A ∪ B) = (C ∖ A)∩(C ∖ B)
C ∖ (B \ A) = (A ∩ C)∪(C ∖ B)
(B ∖ A) ∩ C = (B ∩ C) ∖ A = B∩(C ∖ A)
(B ∖ A) ∪ C = (B ∪ C) ∖ (A ∖ C)
A ∖ A = ∅
∅ ∖ A = ∅
A ∖ ∅ = A

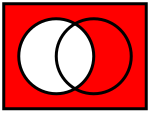
Batzuetan, multzoak multzo unibertsal baten barnean har daitezke. Multzo unibertsal horren eta bere azpimultzo baten arteko multzo osagarri erlatiboari multzo osagarria deitzen zaio. Idazkerari dagokionez, U multzo unibertsala baldin bada eta A azpimultzo bat, A-ren osagarria U - A, U ∖ A, ∁_UA, A^∁ edo A' idazten da. Multzo osagarrien hainbat propietate honakoak dira:

A ∪ A' = U
A ∩ A' = ∅
(A')' = A
U' = ∅
A ⊆ B baldin bada, orduan B ' ⊆ A'
De Morganen legeak
- (A ∪ B)' = A ' ∩ B'
- (A ∩ B)' = A ' ∪ B'

Multzo osagarrien eta osagarri erlatiboen artean hurrengoak betetzen dira:

A ∖ B = A ∩ B'
(A ∖ B)' = A' ∪ B

Ondokoa beti betetzen da:

A ∪ B = (A \ B) ∪ (A ∩ B) ∪ (B \ A)

Biderkadura kartesiarra[aldatu | aldatu iturburu kodea]

A eta B bi multzoren arteko biderkadura kartesiarra, A × B, a eta b elementuek osatzen dituzten (a, b) bikote ordenatuen multzoa da, non a ∈ A eta b ∈ B:

$A\times B=\{(a,b)\,/\,a\in A\,,\,b\in B\}$

Adibideak:

{1, 2} × {gorria, zuria, berdea} = {(1, gorria), (1, zuria), (1, berdea), (2, gorria), (2, zuria), (2, berdea)}.
{1, 2} × {1, 2} = {(1, 1), (1, 2), (2, 1), (2, 2)}.
{a, b, c} × {d, e, f} = {(a, d), (a, e), (a, f), (b, d), (b, e), (b, f), (c, d), (c, e), (c, f)}.

Multzoak finituak badira (kardinala finitua baldin bada), biderkadura kartesiarraren kardinala bi kardinalen biderkadura da:

$|A\times B|=|A||B|$

Biderkadura kartesiarrak propietate hauek betetzen ditu: (Izan bitez A,B,C,D $\subset$ X)

A × ∅ = ∅
$A\times (B\cap C)=(A\times B)\cap (A\times C)$
A × (B ∪ C) = (A × B) ∪ (A × C)
Baldin $c\neq \emptyset$ eta $A\times C=B\times C$ badira, orduan $A=B$
$A\times (B-C)=(A\times B)-(A\times C)$
$(A\times B)\cap (C\times D)=(A\cap C)\times (B\cap D)$
baldin $B\subset C$ bada, orduan $A\times B\supset A\times C$
$(A\times B)\cap (C\times D)=(A\times D)\cap (C\times B)$
Baldin A,B,C eta D multzo ez hutsak badira, orduan $A\times B\subset C\times D$ da baldin eta soilik eta baldin $A\subset C$ eta $B\subset D$ badira.

De Morganen Legeak[aldatu | aldatu iturburu kodea]

A eta B bi multzo edozein izanik

(A ∪ B)′ = A′ ∩ B′

A eta B-ren bilduraren osagarria A-ren osagarriaren eta B-ren osagarriaren bilduraren berdina da.

(A ∩ B)′ = A′ ∪ B′

A eta B-ren ebakidurarenosagarria A-ren osagarriaren eta B-ren osagarriaren ebakiduraren berdina da.

Multzo-teoria eskolan[aldatu | aldatu iturburu kodea]

Multzo hitzak objektu bilduma moduan grafikoki edo fisikoki ilustratu daitekeen zein formalki adieraz daitekeen eraikuntza mental bat da. Eskola-matematiketan, multzo kontzeptua mailaka-mailaka sortzen eta eraikitzen joan behar da, hasieran ahozko hizkuntza eta aurrerago hizkuntza sinboliko berezia erabiliz.

Zenbaki natural kontzeptua elementu kopurua edo kardinal berdina duten multzoen propietatearen balio partikularra adierazteko erabiliko da. Horrela kontaketarako ezinbestekoa da zenbakien izenen segida ezagutzea eta zenbaki naturalaren eta multzo partikular baten arteko bijekzioa egiteko gaitasuna izatea.

Erreferentziak[aldatu | aldatu iturburu kodea]

↑ Jain, P. K.. (1995). Functional analysis. New Age International ISBN 81-224-0801-X. PMC 896658402. (Noiz kontsultatua: 2021-11-07).
↑ Goldberg, Samuel. (1986). Probability : an introduction. (Dover ed. argitaraldia) Dover Publications ISBN 0-486-65252-1. PMC 14356858. (Noiz kontsultatua: 2021-11-07).
↑ Introduction to algorithms. (2nd ed. argitaraldia) MIT Press 2001 ISBN 0-262-03293-7. PMC 46792720. (Noiz kontsultatua: 2021-11-07).
↑ Inklusioak erlazio erreflexiboa, antisimetrikoa eta trantsitiboa betetzen dituenez, ordena partzialeko erlazioa da.
↑ Moschovakis, Yiannis N.. (1994). Notes on set theory. Springer-Verlag ISBN 0-387-94180-0. PMC 28926242. (Noiz kontsultatua: 2021-11-07).
↑ Lucas, John F.. (1990). Introduction to abstract mathematics. (2nd ed. argitaraldia) Ardsley House ISBN 0-912675-73-X. PMC 22951554. (Noiz kontsultatua: 2021-11-07).