Eszentrikotasun orbital

Objektu astronomiko baten eszentrikotasun orbitala da, hain zuzen, beste gorputz baten inguruan duen orbita zenbat desbideratzen den zirkunferentzia perfektu batetik kuantifikatzen duen parametroa. Horrela, 0 balioa orbita zirkular bati dagokio; 0 eta 1en arteko balioak orbita eliptikoei dagozkie; 1 orbita parabolikoa edo ihes orbita da, eta 1 baino balio handiagoak orbita hiperbolikoak dira.

Terminoak sekzio konikoen parametroen terminologiatik hartzen du izena, zeren Kepler orbita bakoitza sekzio konikoa baita. Normalean, bi gorputzen arazo isolatuetarako erabiltzen da, baina galaxian zehar Klemperer-en erroseta itxurako orbita bat jarraitzen duten objektuetarako luzapenak daude.

Definizioa

Distantziaren araberako alderantzizko lege koadratiko baten arabera, indar zentral batek gobernatzen duen bi gorputzeko problema batean, gorputzek Kepler orbitei dagozkien ibilbideak deskribatzen dituzte. Orbita horien eszentrikotasuna haien forma definitzen duen zenbaki ez negatiboa da.

Eszentrikotasunak balio hauek har ditzake:

Orbita zirkularra : e = 0
Orbita eliptikoa : 0 < e < 1 (ikus elipsea )
Bide parabolikoa : e = 1 (ikus parabola )
Bide hiperbolikoa : e > 1 (ikus hiperbola )

E eszentrikotasun orbitala honek ematen du:

e={\sqrt {1+{\frac {2EL^{2}}{m_{\text{red}}\alpha ^{2}}}}}

non E energia orbital osoa den, L momentu angeluarra, m_gorria masa murriztua eta α fisika klasikoko grabitatearen edo elektrostatika bezalako indar zentral baten alderantzizko lege karratuaren koefizientea:

F={\frac {\alpha }{r^{2}}}

(α negatiboa da indar erakargarri baterako, eta positiboa, indar aldaratzaile baterako; ikus Keplerren problema ere)

edo grabitate-indar baten kasuan:

e={\sqrt {1+{\frac {2\varepsilon h^{2}}{\mu ^{2}}}}}

non ε energia orbital espezifikoa den (energia osoa masa murriztutik zatitua); μ masa osoan oinarritutako grabitazio-parametro estandarra da, eta h momentu angeluar erlatibo espezifikoa (momentu angeluarra masa murriztutik zatitua).

0tik 1era bitarteko e balioetarako, orbitaren forma gero eta elipse luzeagoa (edo zapalduagoa) da; 1etik infinitura bitarteko e balioetarako, orbita $2\operatorname {arccsc} e$ bira osoa egiten duen hiperbolaren adar bat da, 180 gradutik 0 gradura jaisten dena. e 1en berdina denean, elipse baten eta hiperbolaren arteko kasu mugatzailea parabola da.

Bide erradialak eliptiko, paraboliko edo hiperboliko gisa sailkatzen dira orbitaren energiaren arabera, ez eszentrikotasunaren arabera. Orbita erradialek momentu angeluar nulua dute, eta, beraz, eszentrikotasun bera dute. Energia konstante mantenduz eta momentu angeluarra murriztuz, orbita eliptiko, paraboliko eta hiperbolikoek dagokion bide erradial motara jotzen dute, e 1era jotzen duen bitartean (edo, parabolikoaren kasuan, 1 izaten jarraitzen du).

Indar aldaratzaile baterako, bide hiperbolikoa baino ez da aplikagarria, bertsio erradiala barne.

Orbita eliptikoetarako, proba sinple batek erakusten du ( $\arcsin e$ ) zirkulu perfektu baten proiekzio-angelua ematen duela e eszentrizikotasuna duen elipse baten gainean. Adibidez, Merkurio planetaren orbitaren eszentrikotasuna ikusteko (e = 0,2056), $\arcsin$ kalkulatu besterik ez dago 11,86 graduko proiekzio-angelua aurkitzeko. Ondoren, edozein objektu zirkularra (adibidez, goitik ikusitako kafe-kikara) angelu horretara okertuz, itxurazko elipseari eszentrikotasun bera emango zaio begiz.

Etimologia

Eszentrikotasun hitza Erdi Aroko latinezko excentricus-etik dator, antzinako grezieratik eratorria ἔκκεντρος ekktros zentrotik kanpo; ἐκ- ek-tik «kanpotik» + κέντρον kentron «zentroa». Eszentrikotasun terminoa Euskaltzaindiak 2003an onartu zuen^[1]

Kalkulua

Orbita baten eszentrikotasuna egoera orbitaleko bektoreetatik kalkula daiteke eszentrikotasun bektorearen magnitude gisa:

e=\left|\mathbf {e} \right|

non:

e eszentrikotasunaren bektorea den.

Orbita eliptikoetarako periapsitik eta apoapsiatik ere kalkula daiteke r_p = a(1 − e) eta r_a = a(1 + e), non a ardatzerdi handia den.

{\begin{aligned}e&={{r_{\text{a}}-r_{\text{p}}} \over {r_{\text{a}}+r_{\text{p}}}}\\&=1-{\frac {2}{{\frac {r_{\text{a}}}{r_{\text{p}}}}+1}}\end{aligned}}

nondik:

r_a apoapsian dagoen erradioa den (hau da, orbitatik sistemaren masa-zentrora dagoen distantziarik urrunena eta elipsearen fokua dena).
r_p periapsian dagoen erradioa den (hurbilen dagoen distantzia).

Orbita eliptiko baten eszentrikotasuna periapsisaren eta apoapsiaren arteko erlazioa lortzeko ere erabil daiteke:

{{r_{\text{p}}} \over {r_{\text{a}}}}={{1-e} \over {1+e}}

Lurrarentzat, eszentrikotasun orbitala ≈ 0,0167, apoapsia = afelioa eta periapsia = perihelioa eguzkiarekiko.

Lurraren urteko orbitaren ibilbiderako r_a / r_p ratioa = erradio nagusia / erradio txikia ≈ 1,034 ibilbidearen erdigunearekiko.

Adibideak

Eguzki Sistemaren gorputzen eszentrikotasunak
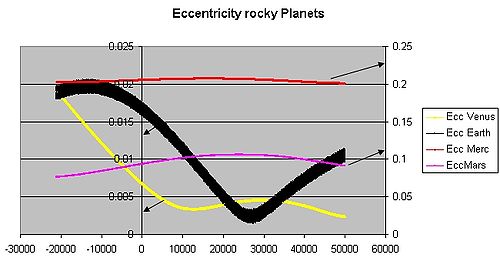
Objektua	Eszentrikotasuna
Tritoia	0.00002
Artizarra	0.0068
Neptuno	0.0086
Lurra	0.0167
Titana	0.0288
Urano	0.0472
Jupiter	0.0484
Saturno	0.0541
Ilargia	0.0549
Ceres	0.0758
(4) Vesta	0.0887
Marte	0.0934
(10) Higiea	0.1146
makemake	0.1559
Haumea	0.1887
Merkurioa	0.2056
(2) Palak	0.2313
Pluton	0.2488
(3) Ekaina	0.2555
(324) Banberga	0.3400
Eris	0.4407
Nereida	0.7507
sedna	0.8549
Halley kometa	0.9671
Hale-Bopp kometa	0.9951
Ikeya-Seki kometa	0.9999
1I/ʻOumuamua	1.20 ^{[ ^[2] ]}

Lurraren orbitaren eszentrikotasuna 0,0167 ingurukoa da gaur egun; Lurraren orbita ia zirkularra da. Artizarrak eta Neptunok eszentrikotasun are txikiagoak dituzte. Ehunka mila urtetan zehar, Lurraren orbitaren eszentrikotasuna 0,0034 eta 0,058 inguru aldatzen da planeten arteko grabitazio-erakarpenen ondorioz (ikus excentricity_graph.html graph)^[3].

Taulan, hautatutako planeta eta planeta nano, asteroide, kometa eta ilargi guztien balioak zerrendatzen dira. Merkuriok Eguzki Sistemako edozein planeten eszentrikotasun orbita handiena du (e = 0,2056). Eszentrikotasun hori nahikoa da Merkuriok perihelioan afelioan baino eguzki-erradiazio bikoitza jasotzeko. 2006ko planetaren berdefinizioaren aurretik, Pluton orbita eszentrikoena zuen planetatzat hartzen zen (e = 0,248). Beste objektu trans-neptuniarrak eszentrikotasun esanguratsua dute; nabarmenki, Eris planeta nanoak (0,44). Are gehiago, Sednak 0,855eko eszentrikotasun ikaragarri altua du bere ustezko afelioa 937 UAkoa eta 76 UA inguruko perihelioa dela eta.

Eguzki Sistemako asteroide gehienek 0 eta 0,35 arteko eszentrikotasun orbitalak dituzte, batez beste, 0,17ko balioarekin^[4]. Haien eszentrikotasun konparatibo handiak, ziurrenik, Jupiterren eraginaren eta iraganeko talken ondorioak dira.

Ilargiaren orbitaren eszentrikotasunaren balioa 0,0549 da, Eguzki Sistemako ilargi handien artean eszentrikoena. Lau ilargiek galilearrek 0,01etik beherako eszentrikotasunak dituzte. Neptunoren Triton ilargiak 1,6e−5 (0,000016) eszentrikotasuna du^[5], Eguzki Sistemako ezagutzen den edozein gorputz eszentrikotasun txikiena; bere orbita gaur egun neur daitekeen zirkulu perfektutik hurbilen dago. Hala ere, ilargi txikiagoek —forma irregularreko sateliteek bereziki— eszentrikotasun handia izan dezakete, Neptunoren hirugarren ilargirik handiena bezala, Nereida, adibidez (0,75).

Kometek eszentrikotasun-balio oso desberdinak dituzte. Kometa periodikoek, normalean, 0,2 eta 0,7 arteko eszentrikotasunak dituzte, baina horietako batzuek orbita eliptiko oso eszentrikoak dituzte, 1etik beherako eszentrikotasunekin. Adibidez, Halley kometak 0,967 balio du. Kometa ez-periodikoak bide ia parabolikoak jarraitzen dituzte, eta 1etik are hurbilago dauden eszentrikotasunak dituzte. Adibide bezala aipa daitezke 0,995 balio duen Hale-Bopp kometa^[6] eta C/2006 P1 (McNaught) 1,000019^[7]. Hale-Boppen eszentrikotasun orbitaren balioa 1 baino txikiagoa denez, bere ibilbidea eliptikoa da, eta, hain zuzen ere, azkenean itzuliko da^[6]. McNaught kometak ibilbide hiperbolikoa du planeten eraginpean dagoen bitartean, baina, oraindik, Eguzkiari lotuta dago, gutxi gorabehera, 10⁵ urteko orbitarekin^[8]. 2010eko garaitik aurrera, C/1980 E1 kometak ezagutzen den edozein kometa hiperbolikoren baino eszentrikotasun handiagoa du, 1,057ko eszentrikotasunarekin^[9], eta Eguzki Sistema utziko du mugagabe.

1I/ʻOumuamua Eguzki Sistematik igarotzen den izarrarteko lehen objektua da. Bere 1,20ko eszentrikotasun orbitalak adierazten du 'Oumuamua ez dela inoiz grabitazioz lotu gure eguzkiarekin. Lurretik 0,2 AUra (30.000.000 km) aurkitu zen, eta, gutxi gorabehera, 200 metroko diametroa du. Bere izarrarteko abiadura (abiadura infinituan) 26,33 km/s-koa da.

Batez besteko eszentrikotasuna

Objektu baten batez besteko eszentrikotasuna da denbora-tarte jakin batean jasaten dituen perturbazio kontuan hartuta batez besteko eszentrikotasuna. Gaur egun, Neptunok 0,0113ko aldiuneko eszentrikotasuna du (2007ko garaia)^[10], baina, 1800 eta 2050 bitartean, bere batez besteko eszentrikotasuna 0,00859an kokatzen da^[11].

Klima efektua

Mekanika orbitalak urtaroen iraupena solstizioaren eta ekinozioaren artean ibiltzen den Lurraren orbitaren eremuarekiko proportzionala izatea eskatzen du; beraz, eszentrikotasun orbitala muturrekoa denean, orbitaren beste muturrean gertatzen diren urtaroak (afelioa) nabarmen luzeagoak izan daitezke. Gaur egun, udazkena eta negua Ipar Hemisferioan, hurbilen dagoenean gertatzen dira (perihelioa), Lurra bere abiadura maximoan mugitzen denean, Hego Hemisferioan alderantziz gertatzen den bitartean. Ondorioz, Ipar Hemisferioan, udazkena eta negua udaberria eta uda baino apur bat laburragoak dira, baina, termino globaletan, hori orekatu egiten da ekuatorearen azpitik luzeagoak izateagatik. 2006an, Ipar Hemisferioko uda negua baino 4,66 egun luzeagoa izan zen, eta udaberria 2,9 egun luzeagoa udazkena baino, orbitaren aldakuntzak direla eta^[12].

Prezesio absidalak ere, poliki-poliki, aldatzen du Lurraren orbitako puntua, non solstizioak eta ekinozioak gertatzen diren. Kontuan izan hori Lurraren orbitan aldaketa motela dela, ez errotazio-ardatzean, ekinozioen prezesioa bezala ezagutzen dena. Datozen 10.000 urteetan, Ipar Hemisferioko neguak, pixkanaka, luzeagoak izango dira, eta udak laburragoak izango dira. Hala ere, hemisferio batean edozein hozte-efektu beste hemisferioaren berotzearekin orekatzen da, eta, aldaketa orokor oro, Lurraren orbitaren eszentrikotasuna ia erdira murriztuko delako konpentsatuko da^[13]. Horrek batez besteko orbita-erradioa murriztuko du, eta bi hemisferioetako tenperaturak glaziar arteko batez besteko gailurretik hurbilago igoko dira.

Exoplanetak

Aurkitutako eguzkiz kanpoko planetetatik, gehienek, gure eguzki-sistemako planetek baino eszentrikotasun orbital handiagoa dute. Eszentrikotasun orbital baxua duten exoplanetak, orbita ia zirkularrak, beren izarretik oso gertu daude, eta mareen akoplamendua erakusten dute izarrarekiko. Eguzki Sistemako zortzi planetek orbita ia zirkularra dute. Aurkitutako exoplanetek erakusten dute eguzki-sistema —bere ezohiko eszentrikotasun baxuarekin— arraroa eta bakarra dela^[14]. Teoria batek eszentrikotasun txiki hori Eguzki Sistemako planeta kopuru handiari egozten dio; beste batek, berriz, iradokitzen du bere asteroide gerriko bereziengatik sortu zela. Beste sistema multiplanetario batzuk aurkitu dira, baina batek ere ez du Eguzki Sistemaren antzarik beren sistema planetesimal bereziengatik, eta horrek planetak orbita ia zirkularrak izatera eraman zituen. Eguzki planetesimalen sistemek asteroideen gerrikoa, Hilda Taldea, Kuiper gerrikoa, Hills Hodeia eta Oort Hodeia hartzen dituzte bere baitan. Aurkitutako exoplaneta-sistemek ez dute sistema planetesimalik, edo oso handia da. Eszentrikotasun baxua beharrezkoa da bizigarritasunerako, batez ere, bizi-forma konplexuen kasuan. Aniztasun handiko planeta-sistemek exoplaneta bizigarriak izateko aukera handia dute^[15]^[16]. Eguzki Sistemaren bira-hipotesi handiak ere beren orbita ia zirkularrak eta beste ezaugarri berezi batzuk ulertzen ere laguntzen du^[17]^[18]^[19]^[20]^[21]^[22]^[23]^[24].

Ikus ere

Erreferentziak

↑ https://www.euskaltzaindia.eus/index.php?sarrera=eszentrikotasun&antzekoak=ez&option=com_hiztegianbilatu&view=frontpage&layout=aurreratua&Itemid=410&lang=eu&bila=bai
↑ ʻOumuamua nunca estuvo ligado al Sol.
↑ A. Berger. (1991). Graph of the eccentricity of the Earth's orbit. Illinois State Museum (Insolation values for the climate of the last 10 million years).
↑ Asteroids. .
↑ David R. Williams. (22 de enero de 2008). Neptunian Satellite Fact Sheet. NASA.
↑ ^a ^b JPL Small-Body Database Browser: C/1995 O1 (Hale-Bopp). .
↑ JPL Small-Body Database Browser: C/2006 P1 (McNaught). .
↑ Comet C/2006 P1 (McNaught) - facts and figures. Perth Observatory in Australia 22 de enero de 2007.
↑ JPL Small-Body Database Browser: C/1980 E1 (Bowell). .
↑ Williams, David R.. (29 de noviembre de 2007). Neptune Fact Sheet. NASA.
↑ Keplerian elements for 1800 A.D. to 2050 A.D.. JPL Solar System Dynamics.
↑ «Equatorial insolation: from precession harmonics to eccentricity frequencies» Clim. Past Discuss. 2 (4): 519–533. doi:10.5194/cpd-2-519-2006..
↑ Arizona U., Long Term Climate
↑ exoplanets.org, ORBITAL ECCENTRICITES, by G.Marcy, P.Butler, D.Fischer, S.Vogt, 20 Sept 2003
↑ «Exoplanet orbital eccentricity: multiplicity relation and the Solar System» Proc Natl Acad Sci U S A 112: 20–4. doi:10.1073/pnas.1406545111. OCLC .4291657 PMID 25512527. Bibcode: 2015PNAS..112...20L..
↑ Steward Observatory, University of Arizona, Tucson, Planetesimals in Debris Disks, by Andrew N. Youdin and George H. Rieke, 2015
↑ Jupiter's Youthful Travels Redefined Solar System. NASA.
↑ «How Did Jupiter Shape Our Solar System?» Universe Today.
↑ Jupiter's 'Smashing' Migration May Explain Our Oddball Solar System. Space.com.
↑ «Mysteries of the asteroid belt» The History of the Solar System.
↑ «The Grand Tack» PlanetPlanet.
↑ «Water delivery and giant impacts in the 'Grand Tack' scenario» Icarus 239: 74–84. 2014 doi:10.1016/j.icarus.2014.05.009. Bibcode: 2014Icar..239...74O..
↑ Loeb, Abraham; Batista, Rafael; Sloan, David. (agosto de 2016). «Relative Likelihood for Life as a Function of Cosmic Time» Journal of Cosmology and Astroparticle Physics doi:10.1088/1475-7516/2016/08/040. Bibcode: 2016JCAP...08..040L..
↑ ^{[Esteka hautsia]}

Irakurketa gehiago

Prussing, John E.; Conway, Bruce A. (1993). Orbital Mechanics. New York: Oxford University Press. ISBN 0-19-507834-9.

Kanpo estekak

Fisikaren mundua: eszentrikotasuna
Climate Forcing Data-ri buruzko NOAA orrialdeak-n Artxibatua 2008-04-30eko datuak (kalkulatuak) biltzen ditu. Lascar et al. (2004) Lurraren orbita aldaketei buruz, azken 50 milioi urteetako eta datozen 20 milioi urteetako eszentrikotasuna barne hartzen du.
Varadi, Ghil eta Runnegar (2003) egindako simulazio orbitalak Lurraren eszentrikotasun orbitala eta orbitaren inklinaziorako serieak eskaintzen ditu.
Keplerren Bigarren legearen simulazioa

Datuak: Q208474

[1] ttps://www.euskaltzaindia.eus/index.php?sarrera=eszentrikotasun&antzekoak=ez&option=com_hiztegianbilatu&view=frontpage&layout=aurreratua&Itemid=410&lang=eu&bila=bai

[2] ʻOumuamua nunca estuvo ligado al Sol.

[Berger1991-3] A. Berger. (1991). Graph of the eccentricity of the Earth's orbit. Illinois State Museum (Insolation values for the climate of the last 10 million years).

[4] Asteroids. .

[Triton-5] David R. Williams. (22 de enero de 2008). Neptunian Satellite Fact Sheet. NASA.

[Hale-Bopp-jpl-6] JPL Small-Body Database Browser: C/1995 O1 (Hale-Bopp). .

[McNaught-jpl-7] JPL Small-Body Database Browser: C/2006 P1 (McNaught). .

[Perth-8] Comet C/2006 P1 (McNaught) - facts and figures. Perth Observatory in Australia 22 de enero de 2007.

[C/1980E1-jpl-9] JPL Small-Body Database Browser: C/1980 E1 (Bowell). .

[nssdc-Neptune-10] Williams, David R.. (29 de noviembre de 2007). Neptune Fact Sheet. NASA.

[ssd-mean-11] Keplerian elements for 1800 A.D. to 2050 A.D.. JPL Solar System Dynamics.

[12] «Equatorial insolation: from precession harmonics to eccentricity frequencies» Clim. Past Discuss. 2 (4): 519–533. doi:10.5194/cpd-2-519-2006..

[13] Arizona U., Long Term Climate

[14] xoplanets.org, ORBITAL ECCENTRICITES, by G.Marcy, P.Butler, D.Fischer, S.Vogt, 20 Sept 2003

[15] «Exoplanet orbital eccentricity: multiplicity relation and the Solar System» Proc Natl Acad Sci U S A 112: 20–4. doi:10.1073/pnas.1406545111. OCLC .4291657 PMID 25512527. Bibcode: 2015PNAS..112...20L..

[16] Steward Observatory, University of Arizona, Tucson, Planetesimals in Debris Disks, by Andrew N. Youdin and George H. Rieke, 2015

[Zubritsky_2011-17] Jupiter's Youthful Travels Redefined Solar System. NASA.

[Sanders_2011-18] «How Did Jupiter Shape Our Solar System?» Universe Today.

[Choi_2015-19] Jupiter's 'Smashing' Migration May Explain Our Oddball Solar System. Space.com.

[Davidsson_2014-20] «Mysteries of the asteroid belt» The History of the Solar System.

[Raymond_2013-21] «The Grand Tack» PlanetPlanet.

[O'Brien_2014-22] «Water delivery and giant impacts in the 'Grand Tack' scenario» Icarus 239: 74–84. 2014 doi:10.1016/j.icarus.2014.05.009. Bibcode: 2014Icar..239...74O..

[23] Loeb, Abraham; Batista, Rafael; Sloan, David. (agosto de 2016). «Relative Likelihood for Life as a Function of Cosmic Time» Journal of Cosmology and Astroparticle Physics doi:10.1088/1475-7516/2016/08/040. Bibcode: 2016JCAP...08..040L..

[24] {[Esteka hautsia]}

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]