Fluido
Fluidoa edo jariakina deritzo ezaugarri nagusi hau duen ingurune material deformagarriari: materiaren ingurune segida berezia da, partikulen artean kohesiozko erakarpen-indar ahula daukana. Horren ondorioz, fluidoen ezaugarrietako bat forma-aldagarritasuna da; baina formaz aldatuz gero, fluidoek ez dute hasierako forma berreskuratzeko gaitasunik; hain zuzen, izaera horretan bereizen dira solido deformagarrietatik, azken horiek hasierako forma berreskuratzeko gaitasuna baitute, barneko kohesio-indarrak direla eta.
Funtsezko ezaugarria jariatzeko gaitasuna dute, alegia, dauden ontzitik isurtzekoa; horregatik, jariakin ere esaten zaie. Dena den, jariakin terminoa Biologiaren arloan erabiltzen da, «zelulek edo edo guruinek ekoizten eta jariatzen duten likido edo substantzia» adierazteko.[1] Nolanahi ere, Fisikan fluido terminoa hobesten da.[2]
Fluidoen propietate berezia biskositatea da, eta fluidoko molekulen arteko barne-marruskaduraren ondorioz sortzen da. Biskositatearen kausaz, fluidoek erresistentzia oposatzen diete barneko esfortzu tangentzialei —ebakidura-tentsio edo zizailadura-esfortzu ere esaten zaie—, eta horrela zaildu edo moteldu egiten da fluido-geruzen arteko higidura erlatiboaren kausaz sortzen den deformazioa.
Fluidoko partikulak elkarrekin finko bilduta mantentzeko ontzi batean gorde behar da fluidoa, hormen artean mugaturik; ontzi barruan egon ezean, zabaltzeko joera dute. Nolanahi ere, fluidoen artean likidoak eta gasak bereizten dira. Likidoek dauden ontziaren forma hartzen dute, eta bolumen konstantea dute ontziz aldatzean. Ordea, gasek ez dute bolumen zehatzik, eta ontzi itxiaren forma eta bolumena hartzen dute; gainera, ontzia irekita egonez gero, kanpora ateratzen dira, berez.
Solidoen eta fluidoen portaerak[aldatu | aldatu iturburu kodea]
Kanpoko indarrik gabe geldi daudenean, solidoek beren forma gordetzen dute eta barneko partikulak posizio finkoetan daudela kontsideratzen da. Haatik, fluidoak berez jariatzeko gaitasuna dute, eta geldi eduki ahal izateko, ontzi bateko hormen artean gorde behar dira; bertan, ontziaren forma hartzen dute, baina fluidoen partikulak etengabe ari dira higitzen eta posizioz aldatzen. Halere, desberdintasun bat dago likidoen eta gasen artean: likidoak gordetzean, ez da zertan ontzia erabat bete, hots, ez da beharrezko ontzien goiko estalikirik jartzea eta likidoaren gainazala libre gera daiteke; gasak, ordea, ontzi itxietan gorde behar dira, bestela irten egiten baitira ontzitik. Nolanahi ere, gasen partikulek askoz higikortasun handiagoa dute likidoenak baino.
Kanpotik etien zaizkien indarren eraginpean ere protaera desberdinak dituzte fluidoek eta solidoek. Hain zuzen, hiru motatako portaerak ager daitezke materian: portaera elastikoa, biskosoa eta plastikoa.
- Portaera elastikoa duten solidoetan indarraren eraginez espantsiozko (edo konpresiozko) esfortzua egiten den bitartean, materia deformatu egingo da —luzatuz edo laburtuz, hurrenez hurren—. Baina indarra desagertzean, objektua hasierako itxura eta tamainara itzuliko da. Portaera hori elastikotasun-mugaraino iristen da.
- Portaera biskosoa duten fluidoetan, ordea, indarraren eraginez fluidoa jariatu ondoren indarra desagertzean, fluidoa hartutako itxura eta forman geratuko da hormen artean.
- Portaera plastikoa honelaxe agertzen da solidoetan: kanpoko indarrek eragindako barne-tentsioa solidoaren elastikotasun-muga baino handiagoa bada, barneko tentsioaren eraginez materia hori biskoso bihurtzen da, eta hortik aurrerako deformazioa iraunkor mantentzen da.
Fluidoen definizioa[aldatu | aldatu iturburu kodea]
Definizioz, fluidoak ebakidura-tentsioen eraginpean etengabe deformatzen diren substanziak dira, ebakidura-tentsio horiek nahi bezain txikiak izanik ere; han zuzen ere, horretan bereizten dira solidoetatik. Ebakidura-tentsioa deritzo fluidoaren edozein barne-gainazaletan eragiten ari den indarraren osagai tangentzialaren eta gainazal horren azaleraren arteko zatidurari:
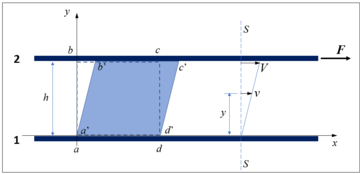
Fluido kontzeptuaren definizioa ulertzeko, adibide sinplifikatu batez baliatuko gara. Kontsidera dezagun bi xafla horizontal paraleloren artean (alboko irudiko eta xaflak) dagoen fluidoa. Demagun xafla geldi dagoela lurraren gainean eta xaflan indarra eragiten ari dela horizontalki. Kontsideratuko dugu ezen xaflak nahikoa luze eta zabalak direla, hegaletako efektuak arbuiatu ahal izateko moduan. Indarrak balioko ebakidura-tentsioa sortuko du ( delakoa xaflen azalera izanik) goiko xaflekin kontatuan dagoen fluidoko goiko geruzan.
Indarra txikia izan arren, goiko xafla abiadura konstantez higiarazten badu, xaflen arteko substantzia fluidoa dela esaten da. Izan ere, indarraren eta fluidoaren partikulen arteko barne-marruskaduraren kausaz lortzen da abiadura konstantea. Gure adibidean, goiko xaflak abiadura lortuko du, eta beheko xafla geldi egongo da lurgainean. Xaflen arteko altuerako puntuek abiadura izango dute, irudian ageri den banaketaren arabera. Horixe da fluido kontzeptuaren definizioaren esanahia.
Biskositatea[aldatu | aldatu iturburu kodea]
Fluidoaren barne-marruskadura hori biskositatea (edo likatasuna) deritzon magnitude fisikoaren bidez kuantifikatzen da[3]. Irudiko fluidoaren kasuan, erlazio hau betetzen da ebakidura-tentsioaren, geruzetako altueren eta fluidoko partikulen abiaduren artean.
Dena den, hori adibideko kasu partikularrari dagokio, Baina erraz orokor daiteke definizioa edozein fluidoren kasurako. Horretarako, fluidoko elementu diferentzial bat kontsideratu behar da fluidoko edozein punturen inguruan. Puntu horretan ondoko erlazio matematiko hau definituko dugu ebakidura-tentsioaren eta deformazioaren abiadura angeluarraren artean:
Erlazio horretan ageri den magnitudeari biskositatea deritzo, definizioz. Biskositatea fluidoen propietate fisiko bat, eta fluido bakoitzaren kasuan, beraren balioa aldatu egiten da tenperaturarekin. Dena den, likidoen eta solidoen portaerak desberdinak dira horretan: likidoen kasuan, biskositatea asko txikiagotzen da tenperatura igotzean; gasen kasuan, berriz, pixka bat handiagotzen da.
Biskositate dinamikoa eta biskositate zinematikoa[aldatu | aldatu iturburu kodea]
Praktikan bi motatako biskositate-koefiziente erabiltzen dira:
- Biskositate dinamikoa —biskositate absolutua ere deitua— aurreko definizioan erabilitako magnitudea da. Beraz, definizioz, fluidoaren oinarrizko elementuak jasaten duen ebakidura-tentsioaren eta horren eraginezko deformazio angeluarraren arteko zatidura da:
- Biskositate zinematikoa deritzon magnitudea biskositate dinamikoaren eta fluidoaren dentsitatearen arteko zatidura da, hots:non fluidoaren dentsitatea den. Fluidoen garraioko kalkuluetan biskositate zinematikoa erabili ohi da, zeren garraiatzen den fluidoaren masa-unitateko energia-galerekin lotuta baitago eta hori oso kontuan hartzekoa da fluidoak banatzeko hodien diseinuan.
Biskositatearen dimentsioa eta unitateak[aldatu | aldatu iturburu kodea]
Biskositatearen definizioko ekuaziotik erraz lor daiteke magnitudearen dimentsio-ekuazioa:sinboloaz adierazten da.
Nazioarteko SI unitate-sisteman biskositate dinamikoaren unitateari poiseuille deritzo. Unitate eratorria da eta balio hau du oinarrizko unitateen funtzioan:
Ondoko taulan zenbait fluido arrunten biskositatearen balioak adierazten dira, tenperaturaren arabera.
| Zenbait materialen
biskositate dinamikoa () | |||
|---|---|---|---|
| Tenperatura
() |
Errizino-olioa
() |
Ura
() |
Airea
() |
| 0 | 53 | 1,792 | 171 |
| 20 | 9,86 | 1,005 | 181 |
| 40 | 2,31 | 0,656 | 190 |
| 60 | 0,80 | 0,469 | 200 |
| 80 | 0,30 | 0,357 | 209 |
| 100 | 017 | 0,284 | 218 |
Taulako datuetan ikus daitekeenez, oliaren eta uraren kasuetan —likidoak— biskositatea moteldu egiten da tenperatura igotzean; oredea, airearen kasuan —gasa— areagotu egiten da.
Fluidoen sailkapena[aldatu | aldatu iturburu kodea]
Oro har, tenperatura jakin batean ere, fluidoen biskositatearen balioa aldatu egiten da deformazioaren abiadura angeluarraren funtzioan. Menpekotasun horren arabera, mota desberdinetako fluidoak daude.
Sailkapena egiteko, aurreko ataleko adibideko fluido-mota sinpleenetik abiatuko gara, alegia, biskositate konstantea duen fluidotik. Kasu horretan, hauxe da fluido-elementu diferentzialaren eta jasaten duen ebakidura-tentsioaren arteko erlazioa:

Hiru eratako fluidoak daude sailkaturik:
- Fluido newtondarrak. Izenak berak adierazten duenez, fluido horiek zehazki betetzen dute Newtonen legea, edo bestela esanda, biskositate-koefizienteak ez du ebakidura-tentsioaren menpekotasunik.
- Fluido idealak. Barne-marruskadurarik gabeak dira. Berez, fluido newtondarren kasu berezia dira; bestela esanda, biskositate-koefiziente nulua dute, hots, da.
- Fluido ez-newtondarrak. Fluido horien biskositate-koefizientea ez da konstantea, deformazio angeluarraren menpekotasun ez-lineala baitu.
Alboko grafikoen, fluidoen eta plastikoen portaerak adierazten dira. Ikus daitekeenez, ebakidura-tentsio txikietan plastikoek solidoek bezalako portaera dute, baina muga-tentsio bat gaindituz gero, fluido newtondarren antzera portatzen dira. Substantzia tixotropikoak oso bereziak dira; horietan, muga gainditzean fluido ez-newtondarren antzeko portaera dute.
Superfluidotasuna[aldatu | aldatu iturburu kodea]
Superfluidotasuna propietate oso berezia da, materiaren egoera berezi ba adierazten duena, zeinean biskositatea desagertu egiten den. Bestela esanda, superfluidotasuneko egoeran biskositatea nulua da, halako moldez non zirkuitu itxi batean etengabe jariatzen den inolako marruskadurarik gabe.
Piotr Kapitsa-k, John F. Allen-ek[4] eta Don Misener-ek[5] aurkitu zuten fenomeno fisiko hau 1973an. Fenomeno fisiko hau tenperatura oso baxuetan gertatzen da, zero absolututik hurbil. Arazoa da elementu guztiak solidoturik daudela tenperatura horietan; baina salbuespen bat dago: helioa. Helioak egoera likidoan irauten du biskositate eta guzti, harik eta mugako tenperaturatik beherantz biskositatea desagertzen den eta portaera oso bitxiak gertatzen diren [6][7]
Fluidoen zenbait propietate eta ezaugarri orokor[aldatu | aldatu iturburu kodea]
Jarraian, fluidoen zenbait propietate eta ezaugarri aipatuko dira, solidoetatik bereizten dituztenak:
- Molekulen higidura ez-akotatua. Fluidoak infinituki deformagarriak dira, eta bertako puntu material batek —molekula batek— fluidoaren baitan izan ditzakeen desplazamenduak ez daude mugaturik; horretan bereizten dira solido deformagarrietatik, azken hauetan puntu materialen higidurak askoz mugatuago baitaude. Portaera desberdin horien arrazoia honetan datza: fluidoetako molekulek ez dute oreka-posiziorik; solido gehienen kasuan, ordea, molekula gehienek higidura txikiak egin ditzakete oreka-posizioen inguruan.
- Konprimagarritasuna. Fluido guztiak dira konprimagarriak, baina likidoak eta gasak oso neurri desberdinean. Hain zuzen, likidoak ia konprimaezinak dira, eta gasak, aldiz, oso konprimagarriak. Halere, konprimagarritasunak ez ditu solidoak eta likidoak bereizten, bien konprimagarritasuna antzekoa baita.
- Biskositatea. Gasetako biskositatea likidoetakoa baino askoz txikiagoa da. Fluidoen deformatze-abiaduraren eraginez, likatasunak barne-tentsioak handiagotzea eragin dezake. Ezaugarri horri dagokionez, fluidoek solido biskoelastikoen antza dute.
- Molekulen arteko distantzia luzea. Oro har, fluidoetako molekulen arteko distantziak solidoetakoen arteko distantziak baino handiagoak dira.
- Van der Waals-en indarrak. Indar hauek Johannes Diderik Van der Waals (1837-1923) fisikari holandarrak aurkitu zituen. Atomo edo molekula apolarren arteko erakartze-indar ahulak dira, Londonen indarrak eta dipolo-dipolo indarrak barnean hartzen dituztenak. Bera konturatu zen molekulen bolumenak eta indar intermolekularrak eragin garrantzitsua zutela molekularen barneko karga positibo eta negatiboenbanaketan
- Forma-memoriarik eza. Fluidoak dagoen ontziaren forma hartzen du; baina ontziz aldatzean, fluidoetan ez da sortzen solidoetako berreskuratze-indar elastikoen antzeko indarrik, eta ontzi berriaren formara egokitzen dira. Ezaugarri hau da, fluidoak (likidoak eta gasak) solido deformagarrietatik argien bereizten dituena.
Fluidoen fenomeno fisiko espezifikoak[aldatu | aldatu iturburu kodea]
Lehenago aipatutako biskositateaz gain, badira fluidoak solidoetatik bereizten dituzten beste zenbait fenomeno eta propietate, fluidoen portaera espezifikoa ezaugarritzen dutenak:
Konbekzioa[aldatu | aldatu iturburu kodea]
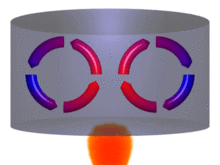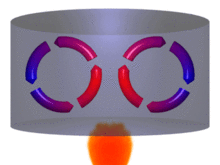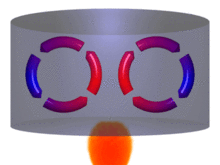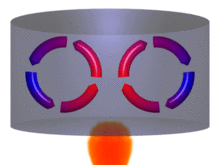
Konbekzioa fluidoetan gertatzen den fenomeno berezi bat da, materian bero-transferentzia izateko hiru moduetako bat da ―beste bi moduak kondukzioa eta erradiazioa―. Fluidoaren barnean, fluidoko partikulen higiduraren bidez transmititzen da beroa tenperatura ezberdineko eskualdeen artean. Izan ere, beroago dagoen eskualdeko fluidoaren bolumena handiagotzean, haren dentsitatea txikiagotu egiten da, eta gainean duen fluidoa dentsoagoa denez, eskualde beroa gorantz doa, eta hotza, beherantz. Horrela, korronte batzuk sortzen dira fluidoaren barnean: konbekzio-korronteak. Hortaz, konbekzioa fluidoaren goranzko eta beheranzko korronteen bidezko beroaren garraioa da.
Konbekzio naturala[aldatu | aldatu iturburu kodea]
Konbekzio naturala fluidoen mekanikaren fenomeno bat da, gradiente batek fluidoan mugimendu bat eragiten duenean gertatzen dena. Gradienteak zenbait magnitude intentsibo har ditzake, hala nola tenperatura (konbekzio termikoa), solutu baten kontzentrazioa (kontzentraziozko konbekzioa) edo gainazal-tentsioa (konbekzio termokapilarra). Tenperatura- edo kontzentrazio-gradientearen araberako dentsitateak dentsitate-diferentziak sortzen ditu fluidoaren barruan. Hori dela eta, Arkimedesen bultzadaren tokitik tokirako aldaketak gertatzen dira, eta horiek eragiten dute konbekzio-korronteak sortzea. Fenomeno ozeanografiko (itsaslasterrak), meteorologiko (ekaitzak), geologiko (magma-igoerak) batzuen jatorria dira.

Konbekzio atmosferikoa[aldatu | aldatu iturburu kodea]
Lurreko atmosferaren konbekzioak urak xurgatutako beroaren kantitate handiak transferitzea dakar. Garapen bertikal handiko hodeiak eratzen ditu (adibidez, kumuluak, eta bereziki kumuluninboak), azken horiek garapen bertikal handiena lortzen duten hodeiak izanik. Hodei horiek ekaitz elektrikoak eta eurite handiak sortzen dituzte. Oso altuera handira iristean ( ingurura) eta tenperatura atmosferiko baxuaren ondorioz bat-batean hoztean, ekaitz elektrikoak, pikortsuak eta euri biziak eragin ditzakete, euri-tantak handituz joaten baitira bortizki igotzean, eta, gero, lurrera erortzen baitira, egoera likidoan edo solidoan. Tamaina handiko onddo asimetriko baten itxura izan dezakete; eta, batzuetan ingude antzeko forma hartuz.
Lurraren atmosferan oso garrantzitsua da konbekzioa eragiten duen prozesua, funtsezko fenomeno batzuk sortzen ditu haizeak azaltzeko eta hodeiak, zikloiak, antizikloiak, prezipitazioak eta abar sortzeko. Bero atmosferikoaren konbekziozko prozesu eta mekanismo guztiak termodinamikaren lege fisikoen araberakoak dira. Prozesu horietatik funtsezkoa da naturako uraren zikloa (ziklo hidrologikoa ere deitua) azaltzen duena.
Gainazal-tentsioa[aldatu | aldatu iturburu kodea]


Fisikan, likido baten kasuan, gainazal-tentsioa deritzo likidoaren gainazala azalera-unitate batez handiagotzeko gehitu beharreko energia-kantitateari. Horrek esan nahi du likidoek aurkako erresistentzia bat egiten diotela beren gainazala handitzeari.

Gainazal-tentsioa dela eta, euskaraz zapatariak deritzen Gerris lacustris intsektuak gai dira uraren gainean ibiltzeko hankak busti eta uretan murgildu gabe; edota metalezko orratz fin bat ur gainean arduraz jarriz gero, orratza bertan gera daiteke uretan murgildu eta hondoratu gabe, orratzaren dentsitatea urarena baino askoz handiagoa izan arren. Fenomeno hau are nabarmenago agertzen da, aldez aurretik orratza koipez igurtziz gero.
Likidoen molekulen arteko kohesio-indarrak ―Van der Waals-en indarrak deritzenak eta likido-egitura posible egiten dutenak, hain zuzen― oso handiak dira distantzia txikietara. Hori dela eta, desberdintasun nabarmena dago, likidoaren barnean edo likidoaren gainazalaren inguruan dauden molekulen egoeren artean.
Likidoaren barneko molekula bakoitza erabat inguraturik daukaten likidoko molekulek, modulu bereko indarrez erakartzen duten norabide guztietan; ondorioz, molekula bakoitzaren gaineko indar erresultante nulua da. Ostera, gainazaletik hurbil dagoen molekularen kasuan, gainazaletiko gora ez du likidoaren molekulen indarrik, eta ondorioz, gainazalaren azpitik dauden molekulen erakarpenaren indar erresultanteak likidoaren barnerantz orientaturik dagoen indar netoa sortzen du. Bestela esanda, kohesio-indarrek barnerantz erakartzen dituzte gainazaleko molekulak, eta berez, likidoari ahalik eta azalerarik txikiena emango liokete.

Likido-tantak[aldatu | aldatu iturburu kodea]
Oro har, tanta deritzo likido-kantitate txiki bati, zeinean, gainazal-tentsioaren eraginez, likidoa gainazal bakarraren barnean dagoen, inolako ontzi soliko batean egon gabe.
Tanten forma[aldatu | aldatu iturburu kodea]

Dimentsio txikiko ur-tantetan (1 mm baino txikiagoetan), gainazal-tentsioa da indar nagusia. Gainazal oso hidrofobiko baten gainean badago, ur-tantak forma esferikoa hartzen du. Oreka-egoera hori gainazalaren azalera minimoari dagokio, alegia, eskala horretan nagusi den gainazal-energiari.
Solidoen gaineko tantak[aldatu | aldatu iturburu kodea]
Forma desberdinak hartzen dituzte tantek, hala nola esferikoa, malko-forma etab. Zenbait magnituderen araberakoak dira fomak: tamaina, pisua, gainazal-tentsioa...
Higitzen ari diren tantak[aldatu | aldatu iturburu kodea]
Tantak higitzen ari direnean, haien forma askoz konplexuagoak dira, sortzen diren hodiaren geometriaren araberakoak. Esate baterako, txorrota batetik erortzen ari diren ur-tantek malko-forma izaten dute bertatik askatu aurretik eta ondoren esfera-forma hartzen dute.
Kapilaritatea[aldatu | aldatu iturburu kodea]
Kapilaritatea (edo kapilartasuna) likido eta solidoen arteko kontaktu-gainazaletan agertzen den propietate bat da, zeinen arabera likidoa gainazaletik gora edo behera egiten duen. Bereziki nabarmena da propietate hori hodi kapilarren barneko likidoetan. Hodi kapilarrak diametro oso txikikoak dira, eta zenbat eta txikiagoak izan, are handiagoa da kapilaritatearen efektua. Kapilaritate-efektuaren intentsitatea fluidoaren gainazal-tentsioaren araberakoa da. Tentsio hori, era berean, fluidoaren kohesioaren araberakoa da, eta hodi kapilar batetik igotzeko edo jaisteko gaitasuna ematen dio.
Likido bat hodi kapilar batetik igotzearen arrazoia da, molekulen arteko indarra edo molekulen arteko kohesioa likidoa hodiaren materialarekin itsasteko indarra baino txikiagoa izatea hau da, bustitzen duen likidoa delako. Likidoak gorantz jarraitzen du, harik eta gainazal-tentsioa eta gorantz igotako likidoaren pisua orekatzen diren arte. Hori da uraren kasua, eta propietate horrek erregulatzen du, hein batean, uraren igoera landareen barruan, grabitatea gainditzeko energia gastatu gabe.
Hala ere, likido baten molekulen arteko kohesioa kapilarrari atxikitzea baino indartsuagoa denean, merkurioaren kasuan bezala, gainazaleko tentsioaren eraginez, likidoa beherantz jaisten da hodi kapilarrean behera, eta haren gainazala konbexua da

Menisko konkabo eta konbexuak[aldatu | aldatu iturburu kodea]
Kapilaritatearen eraginez, "meniskoak" sortzen dira likidoaren eta ontziareen horma solidoen artean. Fisikan, meniskoa deritzo ontziaren hormen kontaktuan likidoaren gainazalak hartzen duen kurbadurari. Kurbadura hori konkaboa ―ahurra ere esaten zaio―(hau da, gora begirakoa) edo konbexua ―ganbila ere esaten zaio― (behera begirakoa) izan daiteke, likidoaren eta ontziaren molekulak elkar erakartzen duten (ura eta beira, adibidez) edo aldaratzen duten (merkurioa eta beira) arabera, hurrenez hurren.
Meniskoaren konkabotasuna sortzen da likidoaren molekulen eta hori duen ontziaren hormen arteko atxikitze-indarrak likidoaren kohesio-indarrak baino handiagoak direnean. Meniskoaren konbexotasuna kohesio-indarrak atxikitze-indarrak baino handiagoak direnean sortzen da.

Difusioa[aldatu | aldatu iturburu kodea]
Fisikan, difusioa edo difusioa molekularra prozesu fisiko itzulezin bat da, zeinean fluido baten barruan dauden partikulen fluxu garbia gertatzen den. Ondorioz, partikulak kontzentrazio handiko eskualde batetik kontzentrazio txikiko eremu batera mugitzen dira, banaketa uniformea lortu arte. Tenperatura- eta kontzentrazio-gradienteek eragiten dute difusioa.
Difusioa gasetan eta likidoetan dauden partikulekin gertatzen da. Kasurako, difusioari esker disoluzio batean dagoen substantzia zabaldu egiten da disolbatzailearen bolumen osora.
Fluidoen portaeran eragina duten magnitude fisikoak[aldatu | aldatu iturburu kodea]
Hainbat magnitude fisiko hartu behar dira kontuan fluido baten portaera aztertu ahal izateko. Oro har, magnitude horien balioak aldatu egiten dira fluidoko puntu batetik bestera. Jarraian, horrelakoen zerrenda ageri da:
- Pisu espezifikoa
- Presioa
- Dentsitatea
- Tenperatura
- Barne-energia
- Entalpia
- Entropia
- Bero espezifikoa
- Eroankortasun termikoa
- Biskositatea
- Kohesioa
Fluidoen higiduraren deskripzioa[aldatu | aldatu iturburu kodea]
Fluidoen higidura deskribatzen duten ekuazioak deribatu partzialetakoak eta ez-linealak dira (Navier-Stokes-en ekuazioak). Oro har, oro korapilatuak dira eta ez daukate soluzio orokorrik. Horregatik, higiduraren deskribapenaren lehenengo hurbilpena egiteko, fluidoen higiduren sailkapen bat egingo dugu lehenik eta behin, horren araberako azalpen kualitatiboak emateko jarraian.
Mota desberdinetako fluxuak[aldatu | aldatu iturburu kodea]

Fluidoa higitzen ari denean, fluidoaren korrontea edo fluxua dagoela esaten da, nahiz eta fluidoen kasuan “fluxu” hitza sekzio batean zehar denbora-unitatean pasatzen den fluido-kantitatea adierazteko ere erabiltzen den. Fluidoen fluxuak saikatzeko, irizpide desberdinak erabiltzen dira.
Biskositatearen eragina kontuan edukirik[aldatu | aldatu iturburu kodea]
- Fluxu turbulentua. Fluidoaren partikulek oso ibilbide irregularrak dituzte, erabat zurrunbilotsuak. Ebakidura-tentsio handiak sortzen dira. Ezin daiteke zuzenki erabil Newton-en biskositate-legea. Energia zinetikoaren galera handia dago (gutxi gorabehera, abiaduraren karratuaren proportzionala).
- Fluxu laminarra. Partikulen higidura xafla antzeko geruza batzuetan gertatzen da, eta geruza bakoitza albokoekiko labaintzen da, beren artean nahastu gabe. Newton-en biskositate-legea betetzen da.
Marruskadura eta konprimagarritasunaren arabera[aldatu | aldatu iturburu kodea]
- Fluxu ideala. Marruskadurarik ez duena eta denbora berean konprimaezina dena. Marruskadurarik ez duenez, biskositate-koefizientea nulua da.
- Fluxu erreala. Fluxu idealaren baldintzak betetzen ez dituena.
Tenperatura eta beroarekiko portaeraren arabera[aldatu | aldatu iturburu kodea]
- Fluxu isotermoa. Kasu honetan ez dago tenperaturaren aldaketarik.
- Fluxu adiabatikoa. Fluidora ez da berorik sartzen eta ez bertatik ateratzen ere. Fluxu adiabatiko itzulgarriari (hau da, marruskadurarik gabeari) isoentropikoa deritzo.
Denborarekiko aldakuntza kontuan edukiz[aldatu | aldatu iturburu kodea]
- Fluxu iraunkorra. Espazioko puntu konkretu batean fluidoaren propietateak eta higidura bera ere denbora osoan berberak direnean, fluxua iraunkorra dela esan ohi da.
- Fluxu ez-iraunkorra edo denborarekiko aldakorra. Aurreko baldintzak betetzen ez direnean, hots, puntu berean denborarekin p, p, T edota v aldatuz doazenean.
Espazioarekiko aldakuntzaren arabera[aldatu | aldatu iturburu kodea]
- Fluxu uniformea. Espazioko puntu guztietan abiadura berbera.
- Fluxu ez-uniformea. Abiadura desberdina puntu desberdinetan. Zer esanik ez, fluxua ez-uniformea izan arren, iraunkorra izan daiteke.
Korronte-lerroak eta korronte-hodiak[aldatu | aldatu iturburu kodea]

Fluxu laminarraren kasuan, oso baliagarria da korronte-lerroa deritzon kontzeptua. Fluidoko puntu bakoitzean abiaduraren norabidearen ukitzailea da, eta erregimen iraunkorrean partikula batek egiten duen bidea adierazten du. Fluxu laminarrean korronte-lerroek ez dute elkar ebakitzen. Ageri denez, honela definituriko korronte-lerroak fluidoaren partikulen abiadurek osaturiko eremu bektorialaren (abiadura-eremua deiturikoaren) eremu-lerroak dira.
Fluxu laminarrean, korronte-lerroekin batera datorren beste kontzeptu bat korronte-hodia da. Lerroekiko zeharki jarritako kurba itxi batetik pasatzen diren korronte-lerro guztiek, korronte-hodi bat osatzen dute Fluxua iraunkorra denean, korronte-hodiak finkoak dira eta horietan ez da fluidorik sartzen ez irteten.

Reynolds zenbakia[aldatu | aldatu iturburu kodea]
Fluxu laminarrean sortzen diren korronte-lerroak zein baldintzatan agertzen diren jakiteko, fluidoko magnitude batzuen balioak kontuan hartzen dituen zenbaki adimentsional bat definitzen da praktikan: Reynolds zenbakia.
Reynolds zenbakia ( sinboloa) fluidoen dinamikan erabiltzen den zenbaki adimentsional bat da. Zenbaki honek indar inertzialen eta indar biskosoen arteko erlazioa ematen du. Horrela, Reynolds zenbaki berdina duten bi egoera dinamikoki antzekoak dira; beraz, tamaina desberdineko objektu-modeloetan oinarriturik, tamaina errealeko objektu errealaren dinamikaren ezaugarriak ondorioztatzenko balio du.
Reynolds zenbakia honelaxe definitzen da:
non fluidoaren abiadura karakteristiko bat den, objektu solidoaren luzera karakteristiko bat eta fluidoaren biskositate zinematikoa.
Reynolds zenbakiaren balio txikietan indar biskosoek nagusitzen dira, eta fluxua laminarra da; ostera, balio handiak dituenean, fluxua turbulentua bihurtzen da. Hodi batetik higitzen ari diren likidoen kasuan denean fluxua laminarra izaten da eta denean, turbulentua; tarteko balioetan hodiaren eta likidoaren propietateen araberako izaten da.
Fluxu laminar eta iraunkorra duen fluidoaren higidura aztertzeko ekuazioak[aldatu | aldatu iturburu kodea]
Fluxu laminar eta iraunkorra duen fluidoaren higidura aztertzeko eta ulertzeko, korronte-lerroak eta korronte-hodiak hartzen dira oinarritzat eta printzipio hauetan oinarrituriko ekuazioak erabiltzen dira.

Jarraitutasunaren ekuazioa[aldatu | aldatu iturburu kodea]
Kontsidera ditzagun korronte-hodi bateko eta sekzio normalak eta barneko korronte-hodi infinitesimal bat. Fluxua iraunkorra bada, sekziotik denbora-unitatean sartzen den masa eta denbora-unitate berean sekziotik irteten dena berdinak dira. Matematikoki idatzirik:

Energiaren ekuazioa korronte-lerro batean. Bernouilliren ekuazioa[aldatu | aldatu iturburu kodea]
Kasu honetan fluxu laminar eta iraunkorra izateaz gain, fluidoa ideala dela kontsideratuko dugu. Hortaz, korronte-lerro batean kontsidera dezagun bertan fluidozko prisma infinitesimal bat (beronen oinarria da, eta altuera, ). Korronte-lerroaren tangentearen norabidean Newton-en bigarren legea ( alegia) erabiliz, bigarren ordenako infinitesinoak arbuiatuz, ekuazio hau lortzen da:
non puntuko presioa den, fluidoaren dentsitatea eta prismaren azelerazioak norabide tangentzialean duen osagaia. Ekuazio hori korronte-lerroan barrena integraturik, Bernouilliren ekuazioa ―Bernouilliren printzipioa ere esaten zaio― lortzen da:
- : puntu horretan fluidoak masa-unitateko duen energia potentziala da.
- : puntu horretan fluidoak masa-unitateko duen energia zinetikoa da.
- : aurreko gaien bi gaien analogia eginez, masa-unitateko presio-energia dela esan dezakegu. Gai hori fluidoen kasuan agertzen da soilik, eta solido elastikoen kasuko energia potentzial elastikoaren antzekoa da. Berez, barne-energia potentzialaren zati bat da.
Hortaz, nolabait esateko, Bernouilliren printzipioak energia mekaniko osoaren kontserbazioa adierazten du, fluxu iraunkorra duen marruskadurarik gabeko fluido ideal konprimaezin baten korronte-lerro bateko puntuen artean.
Erreferentziak[aldatu | aldatu iturburu kodea]
- ↑ https://zthiztegia.elhuyar.eus/terminoa/eu/jariakin,+Zientzia eta Teknologiaren HIztegi Entziklopedikoa..
- ↑ https://zthiztegia.elhuyar.eus/terminoa/eu/fluido,+Zientzia eta Teknologiaren Hiztegi Entziklopedikoa..
- ↑ https://zthiztegia.elhuyar.eus/terminoa/eu/likatasun,+Zientzia eta Teknologiaren Hiztegi Entziklopedikoa..
- ↑ https://en.wikipedia.org/wiki/John_F._Allen_(biochemist),+John F. Allen (biokimikaria)..
- ↑ https://en.wikipedia.org/wiki/Don_Misener,+Don Misener..
- ↑ Ben Miller experiments with superfluid helium - Horizon: What is One Degree? - BBC Two, https://www.youtube.com/watch?v=9FudzqfpLLs&t=51s..
- ↑ Helio superfluidoaren azalpena, https://www.youtube.com/watch?v=2Z6UJbwxBZI&NR..
Bibliografia[aldatu | aldatu iturburu kodea]
- Arabiourrutia Gallastegi, Miriam & Aguado Zarraga, Roberto (2018), Fluidoen mekanika, Euskal Herriko Unibertsitatea, Argitalpen Zerbitzua, ISBN: 978-84-9082-886-1, (eskuratzeko bidea: World Wide Web).
- Etxebarria Bilbao, Jose Ramon (arg.) (2003) Fisika orokorra (2. argitalpena) UEU, Bilbo ISBN 9788484380450.
- J.R. Etxebarria & F. Plazaola (1992) Mekanika eta uhinak, UEU, {{ISBN|84-86967-42-2}}
- Fishbane, Paul (2008) Fisika zientzialari eta ingeniarientzat. 1. bolumena, (1.etik-21.era Gaiak) Universidad del País Vasco/Euskal Herriko Unibertsitatea ISBN9788490820308 PMC932800438.
- Mott, Robert (1996) Mecánica de fluidos aplicada (4ª edición). México: Pearson Educación. ISBN 0-02-384231-8.
- Holzapfel, G. A.|título= Nonlinear Solid Mechanics: A Continuum Approach for Engineering|url= http://books.google.es/books?id=\_ZkeAQAAIAAJ%7Ceditorial=[Betiko hautsitako esteka] John Wiley & Sons|isbn= 9780471823193|año= 2000
















![{\displaystyle [\mu ]={\begin{bmatrix}{\frac {\tau }{{\text{d}}v/{{\text{d}}y}}}\end{bmatrix}}={\begin{bmatrix}{\frac {F/S}{{\text{d}}v/{{\text{d}}y}}}\end{bmatrix}}={\frac {{\text{MLT}}^{-2}{\text{L}}^{-2}}{{\text{LT}}^{-1}{\text{L}}^{-1}}}={\text{ML}}^{-1}{\text{T}}^{-1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c9ce636c6d707ec4e719225e13031a8ceaea5c5)



































