Momentu magnetiko
| Momentu magnetiko | |
|---|---|
| Formula | |
| Formulako ikurra | , , eta |
| Ohiko ikurra | |
| Neurtzeko unitatea | ampere square metre (en) |
| Dimentsioa | |
Momentu magnetikoa ( ) iturri magnetiko baten intentsitatea eta iturri honen ondorioz sortutako dipolo magnetikoaren orientazioa zehazten duen magnitude bektoriala da. Eremu magnetiko hau sortzen duen iturria askotarikoa izan daiteke: iman naturala, korronte elektrikoa duen begizta, elektroia, molekula, planeta etab.
Momentu magnetiko eta eremu magnetikoari magnitude eta noranzko bat dagozkie. Momentu magnetikoaren kasuan, hego polotik ipar polorako noranzkoa du. Eremu magnetikoaren noranzkoa, berriz, iturriaren araberakoa da. Iman baten kasuan, momentu magnetikoaren proportzionala da. Zirkuitu baten kasuan, aldiz, zirkuituaren azaleraren perpendikularra da, eta eskuin-eskuaren araua bidez definitutako noranzkoa du.
Objektu baten momentu dipolar magnetikoa definitu ahal izateko, objektuak eremu magnetiko jakin batean jasandako indar momentuaren menpekoa dela ulertzea beharrezkoa da. Indar momentu honen balioa eta noranzkoa; momentu magnetikoaren balioaren eta eremu magnetikoaren noranzkoarekiko duen orientazioaren menpekoak dira.
Momentu magnetikoaren inguruan hitz egiteko garaian, sistema baten momentu dipolar magnetikoari erreferentzia egiten zaio normalean. Honek eremu magnetiko batek sortutako hedapen multipolarraren lehen gaiari egiten dio erreferentzia. Iman txikien edo distantzia handien kasuan, momentu magnetikoaren lehen gai hau aztertzearekin nahikoa izan ohi da. Objektu puntualak ez diren kasuetan, egitura konplexuagoetan, momentu magnetikoaren gainerako osagaiak erabiltzea beharrezkoa da. Objektu baten eremu magnetikoaren dipolo osagaia bere momentu dipolar magnetikoaren norabidearekiko simetrikoa da, eta objektuarekiko distantziaren karratuarekiko alderantzizko proportzionala da.
Oinarri orokorrak[aldatu | aldatu iturburu kodea]
Definizioa[aldatu | aldatu iturburu kodea]
Momentu magnetikoa, kanpo eremu magnetiko batek objektu baten eremu bektorialarekin izandako elkarrekintzak eratzen duen indar momentuarekin lerrokatuta dagoen bektorea da. Hauen arteko erlazioa honela adierazten da:[1]
- non τ dipoloan eragiten duen indar momentua, kanpo-eremu magnetikoa eta , momentu magnetikoa diren.
Printzipioz, definizio honen oinarria batek lagin ezezagun batean neur dezakeen momentu magnetikoa da. Korronte begizta baterako, definizio hau momentu dipolar magnetikoaren magnitudea berdintzen du korrontearen produktua bider begiztaren azalera. Gainera, definizio horri esker, edozein korronte makroskopiko ezagunen banaketaren itxarotako momentu magnetikoa kalkula daiteke.
Beste definizio bat ere badago, erabilgarria dena momentu magnetikoaren kalkulu termodinamikoetarako. Definizio honetan, sistema baten momentu dipolar magnetikoa bere barne-energiaren gradiente negatiboa da. Gradiente hau kanpo-eremu magnetikoarekiko kalkulatuta dago eta ondorengoa da:
Oro har, barne-energiak sistemaren berezko energia eta sistemaren barne-prozesuen energia hartzen ditu. Adibidez, kanpo-eremu batean 2p egoeran dagoen hidrogeno atomo batentzat, bere berezko energia arbuiagarria da eta, beraz, barne-energia, funtsean, 2p egoeraren energia da; hau da, orbital horretan dagoen elektroiaren Coulomben energia potentziala eta elektroi beraren energia zinetikoa. Barne-dipoloen eta kanpo-eremuen arteko elkarrekintzak sortzen duen energia ez da barne energia horren parte.[2]
Unitateak[aldatu | aldatu iturburu kodea]
Nazioarteko Unitate Sistemako (SI) oinarrizko magnitudeetan funtsatutako unitatea, momentu magnetikorako, da, non A ampere (korrontearen SI oinarrizko unitatea) den eta m metroa (distantziaren SI oinarrizko unitatea) den. Unitate honek SI-tik eratorritako beste unitate batzuetan baliokideak ditu: [3][4]
non N newton (SI sistematik eratorritako indarraren unitatea), T tesla (SI sistematik eratorritako fluxu magnetikoaren dentsitatearen unitatea) eta J joule (SI sistematik eratorritako energiaren unitatea) diren.[5]Indar momentua (N·m) eta energia (J) dimentsioari dagokionez baliokideak izan arren, indar momentuak ez dira inoiz energiaren unitateetan adierazten. [6]
CGS sisteman(sistema metrikoaren aldaera bat non luzera-unitatea zentimetroak diren), elektromagnetismoko zenbait unitate daude non garrantzitsuenak ESU, gaussiarra eta EMU dira. Horien artean, momentu dipolar magnetikoaren ez-baliokideak diren bi magnitude daude:
(EMU)
(Gaussiarrean eta EMU)
non statA estatampereak, cm zentimetroak, erg ergak eta G gauss-ak diren. Baliokideak ez diren CGS-ren bi magnitude hauek (EMU/ESU) hutseango argiaren abiaduraren proportzionalak dira eta, -tan adierazita daude.
Artikulu honetan agertzen diren formula guztiak SI unitateetan zuzenak dira, baina beste unitate sistemetan erabiltzeko aldatzea beharrezkoa izan daiteke. Adibidez, SI sisteman, I korrontea eta A azaleraren momentu magnetikoa IA da (ikus beherago), baina unitate gaussiarretan momentu magnetikoa hurrengoa da: IA/c
Momentu dipolar magnetikoa neurtzeko beste magnitude batzuen artean, Bohr-en magnetoia eta magnetoi nuklearra daude.
Neurketak[aldatu | aldatu iturburu kodea]
Objektuen momentu magnetikoak normalean magnetometro izeneko gailuekin neurtzen dira (edo neurtu ohi dira). Hala ere, magnetometro guztiek ez dute momentu magnetikoa neurtzen: haietako batzuk eremu magnetikoa neurtzeko prestatuta daude. Objektu baten eremu magnetikoa ondo ezagutuz gero, momentu magnetikoa eremu magnetiko horretatik abiatuta kalkulatu daiteke.
Ereduak[aldatu | aldatu iturburu kodea]
Momentu magnetikoaren izaera azaltzeko modua aldatuz joan da denboran zehar. 1950eko hamarkada baino lehen, testuliburuek alegiazko karga magnetikoak erabiltzen zituzten kontzeptua aurkezteko. Harrezkero, Ampereren korrontean [7]oinarritutako definizioak hartu du indarra, azalpenik erabiliena izanik. Izatez, material magnetikoetan momentu magnetikoa elektroien spin eta momentu magnetiko orbitalaren araberakoa da.
Polo magnetikoen eredua[aldatu | aldatu iturburu kodea]

Elektrostatika oinarritzat hartuz, momentu magnetiko iturriak aurkako zeinudun poloen bidez adieraz daitezke. Gilberten eredu[8] izenez ere ezaguna den eredu honetan, moduluz berdinak baina aurkako zeinuak dituzten alegiazko bi monopolo magnetiko erabiltzen dira, iman txiki baten jokaera azaltzeko.
Poloak beti bikoteka azaltzen dira (ez dugu inoiz polo soil bat aurkituko), bakoitza distantziarekin ahultzen den indar magnetiko baten iturri izanik. Bikoteka dauden poloek aurkako zeinuak izanik, batek alderapen indar bat eragiten duen bitartean, besteak indar alderatzaile bat eragingo du, indarrak elkar deuseztatuz.
Iman batek espazioko puntu jakin batean sortutako indarra poloen p indarraren eta haien arteko l distantziaren araberakoa da nagusiki. Bi kontzeptu hauek erabiliz, dipolo magnetiko momentua, m, defini dezakegu.[7]
Bere norabidea Hego Polotik Ipar Polorakoa da. Dipolo magnetikoa ez dugu hartu behar dipolo elektrikoen analogo zehatz bezala, dipolo magnetikoak momentu angeluarrarekin lotuta baitaude. Hala ere, polo magnetikoak oso erabilgarriak dira kalkulu magnetostatikoetarako, bereziki ferroimanen [7]aplikazioetan.
Ampere-begizta eredua[aldatu | aldatu iturburu kodea]

Hans Christian Ørsted-ek korronte elektrikoek eremu magnetiko bat eratzen zutela eta André-Marie Ampère-k korronte elektrikoek imanen antzeko jokaera zutela ondorioztatu ondoren, ohikoa zen eremu magnetikoak korronte elektrikoko begizten ondorio zirela pentsatzea. Ampere-k garatutako eredu honetan, I korrontedun begiztak sortutako dipolo magnetikoa da imanen osagai. Momentu dipolarra,
S begiztaren azalera izanik. Momentuaren noranzkoa eskuin eskuaren araua erabiliz lor genezake.
Korronte banaketa lokalizatuak[aldatu | aldatu iturburu kodea]

Korronte banaketa bat finitua bada eta bertan parte hartzen dituzten korronte guztiak ezagunak badira, sistemaren momentu dipolar magnetikoa kalkula daiteke. Definizioz,
non r posizio bektorea eta j korronte dentsitatea diren. Korronte dentsitatea korronte begizta batez ordezkatuz gero, lerro integrala ebatziz lor daiteke momentua. Aurreko atalean adierazi bezala,
Solenoide baten momentu magnetikoa[aldatu | aldatu iturburu kodea]
S azalera eta N bira dituen solenoide baten guztizko momentu magnetikoa eredu hau orokortuz kalkula daiteke; momentu totala, bira bakoitzean lortutako momentuen batura izanik.

Eredu kuantikoa[aldatu | aldatu iturburu kodea]
Maila mikroskopikoan material edo molekulen momentu magnetikoak aztertzean, komenigarria da mekanika kuantikoa oinarri duen hirugarren eredu bat kontuan izatea, maila atomiko eta molekularrean ematen diren gertaerak ez baitira kontuan hartzen ez polo magnetikoen ereduan, ez ampereren ereduan. Maila makroskopikoan gertatzen den bezala, momentu dipolar magnetikoa eta momentu angeluarra linealki erlazionatuta daude, baina desberdina da partikula bakoitzerako. Gainera, beharrezkoa da momentu angeluar intrintsekoa (spinarena) eta partikularen momentu angeluar orbitala bereiztea.
Kanpo eremu magnetikoaren efektua[aldatu | aldatu iturburu kodea]
Indar momentuaren efektua[aldatu | aldatu iturburu kodea]
m momentu dipolo magnetikoa duen eta B eremu magnetikoaren menpe dagoen objektu baten τ momentuaren adierazpena hurrengoa da:
.
Hau baliozkoa da eremu magnetikoa uniformea den bitartean, edozein korronte-banaketa lokalizatua dela eta. Ostera, eremu magnetiko ez uniformearen kasurako, ekuazioak bakarrik balio du dipolo magnetikoaren erdiguneko momenturako dipolo magnetiko hori nahikoa txikia baldin bada[9].
Eremu magnetiko uniforme batean jarritako elektroi, nukleo edo atomo bat Larmorren maiztasuna izenez ezagutzen den frekuentziaren arabera egingo dute prezesioa. (Ikusi erresonantzia)
Indar baten efektua[aldatu | aldatu iturburu kodea]
Kanpotik sortutako eremu magnetiko baten momentu magnetikoak energia potentziala eragiten du eta adierazpen honen bitartez deskribatzen da:
Kanpotik sortutako eremu magnetikoa ez uniformea denean indar bat sortuko da, eremu magnetikoaren gradientearekiko proportzionala dena eta momentu magnetikoan eragingo duena. Aipatutako indar honek dipolo magnetikoan duen eragina deskribatzeko bi adierazpen existitzen dira, dipolorako erabiltzen den eredua ampere-begizta izatearen ala bi monopolo (dipolo elektrikoaren antzekoa[10]) izatearen arabera.
Beraz, korronte-begiztaren kasuan, indarrerako erabili beharreko adierazpena:
da.
Aldiz, asumituz monopoloa daukagula, erabiliko dugun formula:
da.
Azkenik, horrelako monopolo pare bat badugu, honela aldatuko da aurreko indarraren adierazpena:
Aipatutako adierazpenak elkarren artean erlazionatuz:
Konturatu, kasu guztietan m dipoloa dela eta B dipoloaren posizioko eremu magnetikoa dela eta korronte aldaketarik ala denbora aldaketarik ez balego, ∇×B = 0 eta ∇·B = 0 onartzen direla.
Energia askearekiko erlazioa[aldatu | aldatu iturburu kodea]
Sistema baten momentu magnetikoa sistema horren energia askeakin erlaziona daiteke[11]. eremu magnetikoan gaudela, energia askea sistema baten momentu magnetikoarekin erlaziona daiteke hurrengo adierazpena jarraituz:
non S sistemaren entropia den eta T tenperatura.
Era berean, momentu magnetikoa definitzeko energia askearen terminoetan erabili daitekeen beste adierazpen bat:
.
Magnetismoa[aldatu | aldatu iturburu kodea]
Gainera, kanpotik eragindako eremu magnetiko batek objektuaren beraren momentu magnetikoa alda dezake, adibidez, magnetizatuz. Fenomeno horri magnetismoa deritzo.
Kanpotik aplikatutako eremu magnetiko batek materiala osatzen duten dipolo magnetikoak bira ditzake, paramagnetismoa zein ferromagnetismoa sortuz. Hari beretik, aplikatutako eremu magnetikoak eragina izan dezake eremu magnetikoa sortzen duten korronteetan (orbita atomikoak, adibidez) eta horrela diamagnetismoa sortu.
Efektuak bere ingurunean[aldatu | aldatu iturburu kodea]
Momentu magnetiko baten eremu magnetikoa[aldatu | aldatu iturburu kodea]
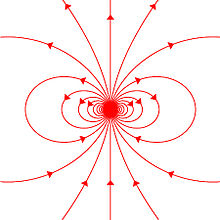
Artikulu nagusia: Dipolo magnetikoa
Baita ere: Dipolo
momentu dipolar magnetikoa duen edozein sistemak; eremu magnetiko dipolarra sortuko du inguratzen duen espazioan. Sortutako eremu magnetiko honek ordena handiagoko osagai multipolarrak izan ahal dituen arren, distantzia handitu ahala ordena txikiagotu egingo da. Honen eraginez, distantzia handiagoko puntuetan, eremu magnetikoaren dipoloaren osagaiak izango du eragin handiena.
Dipolo magnetikoaren eremu magnetikoa; imanaren momentu magnetikoaren () indarraren eta noranzkoaren araberakoa da. Baina, distantziaren kuboarekin alderantziz proportzionala da:
non imanak sortutako eremu magnetikoa den eta dipolo magnetikoaren erditik eremu magnetikoa neurtzen den puntura dagoen distantzia den. Aipatutako distantziaren kuboaren proportzionaltasuna errazago ikus daiteke adierazpenari esker. Non distantzia bektorea, distantziaren balio absolutua eta distantzia bektorearen noranzkoa diren.
eremu magnetikoari dagokion ekuazio baliokidea berdina da baina = 4π×10−7 H/m -rekin biderketa eginez, non hutsaren iragazkortasun magnetikoa den. Adibidez:
Bi dipolo magnetikoren arteko indarrak[aldatu | aldatu iturburu kodea]
Lehen esan bezala, momentua duen dipolo begiztak momentua duen begiztan eragiten duen indarra ondokoa da:
non -en eremu magnetikoa den. Gradientea () kalkulatuz gero: [12][13]
non lehenengo dipolotik bigarrenera dagoen distantziaren noranzkoa den, eta distantzia honen balio absolutua den. Adierazpen baliokide bat honako hau da: [13]
Kasu honetan, -en gainean aplikatutako indarra aurkako noranzkoan egongo da.
Dipolo baten momentuaren eragina beste dipolo batean[aldatu | aldatu iturburu kodea]
Lehenengo dipoloaren indar momentua bigarrenaren gainean hurrengoa da:
Dipolo magnetikoak[aldatu | aldatu iturburu kodea]
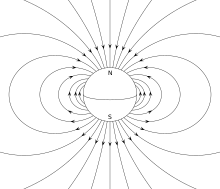
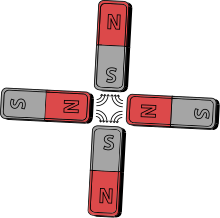
Imanek duten eremu magnetikoaren baldintzen arabera, hainbat eredu ditugu. Eredu bakoitza aurrekoa baino konplexuagoa da. Lehenengo hiru ereduei honela deritze: monopoloa (isolatutako ipar edo hego polo bat), dipoloa ( kontrajarritako bi polo magnetiko berdin) eta kuadropoloa ( kontrajarritako lau polo elkartuz: bi dipolo berdin eta bi aurkako). Eredua zenbat eta konplexuago izan, bakoitzaren eremu magnetikoaren ekarpena bizkorrago txikiagotuko da distantzia handitzerakoan. Honen eraginez, distantzia handietan zeroren desberdina den lehen ekarpenak nagusitasuna hartuko du.
Iman askoren kasuan, nulua ez den lehen ekarpena momentu magnetiko dipolarrarena da. Orain arte, ez da isolatutako monopolo magnetikorik esperimentalki hauteman. Dipolo magnetikoa korronte begizta baten edo polo bikote baten muga da, baldin eta iturriaren balioa zerora hurbiltzen bada eta momentua konstante mantentzen bada. Muga hauek iturritik urren dauden eremu magnetikoei aplikatuz gero baliokideak izango dira. Baina adibide bakoitzak barne-eremuentzat aurreikuspen desberdinak eskaintzen ditu. (Ikusi jarraian).
Potentzial magnetikoak[aldatu | aldatu iturburu kodea]
Tradizionalki, momentu dipolar magnetikoaren ekuazioak (eta ordena handiagoko osagaiak) potentzial magnetikoaren[14] balio teorikoetatik lortutakoak izan ohi dira, matematikoki eremu magnetikoa baino sinpleagoak direlako ebazteko orduan.
Polo magnetikoaren ereduan garrantzia duen eremu magnetikoa eremu desmagnetizatzailea da. Definizioz, korronte askeen eraginez sortutako eremuak ez duenez -ren zati desmagnetizatzailean parte hartzen, hurrengo potentzial eskalar magnetikoa existitzen da:
Ampere-begiztaren ereduan, berriz, garrantzia duen eremu magnetikoa indukzio magnetikoa da. Monopolo magnetikoak existitzen ez direnez, potentzial bektore magnetiko hau existitzen da:
Bi potentzial hauek ausazko edozein korronte-banaketatarako (ampere-begiztaren ereduan) edo edozein karga magnetikoaren banaketatarako (polo magnetikoaren ereduan) erabil daitezke, baldin eta soilik baldin eskualde murriztu baterako hurrengo ekuazioak betetzen badira:
Non korronte dentsitatea den (ampere-begiztaren ereduan), polo magnetikoaren indar dentsitatea (potentzial elektrikoaren moduan erabiltzen den karga dentsitatearen elektrikoaren modukoa) eta integralak osatzen duten koordenatuen bolumenarekiko.
Hedapen multipolarra erabiliz, hurrengo hurbilpena lortu dezakegu, non; lehen osagai ez nuluak distantzia handietan eragin handiena duen. Hona hemen potentzial bektorearen lehen osagai ez nulua:
jarraian adierazitako formularen bidez lortu daiteke:
Non biderketa bektoriala den, posizio bektorea eta korronte elektrikoaren dentsitatea. bolumen integrala aplikatuz.
Polo magnetikoaren ikuspuntutik, potentzial eskalarraren lehen osagai ez nulua:
Hemen adierazitako polo magnetikoaren indar dentsitatearen bidez erlaziona daiteke, baina magnetizazioarekin erlazionatuz gero erabilgarriagoa da:
Bi ekuazioetan m ikurra erabiltzen da, bien emaitza berdina delako imanaren kanpo-eremuan.
Momentu dipolarrak eratutako kanpo-eremu magnetikoak[aldatu | aldatu iturburu kodea]
Dipolo magnetiko baten fluxu magnetikoaren dentsitatea ampere-begiztaren ereduan hurrengoa da:
Eremu magnetikoaren indarrari dagokionez, berriz,
Dipoloaren barne-eremu magnetikoa[aldatu | aldatu iturburu kodea]
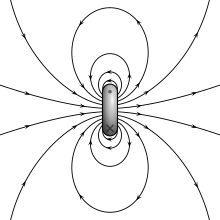
Aipatutako dipoloaren bi ereduek (korronte begizta eta polo magnetikoak) emaitza berdinak dituzte iturritik distantzia handira sortutako eremu magnetikoari dagokionez. Baina iturriaren barnean emaitza desberdinak ematen ditu eredu bakoitzak. Poloen arteko eremu magnetikoa (Ikusi polo magnetikoa definitzeko irudia) momentu magnetikoaren aurkako noranzkoan dago (karga negatibotik positibora doa). Korronte begiztaren barnealdeari dagokionean, berriz, momentu magnetikoaren noranzko berbera du. Barne eremu hauei dagozkien mugak ezberdinak dira halaber, baina material magnetikoaren barneko eremu magnetikoak kalkulatzeko soilik dira erabilgarriak.[15]
Dipolo magnetikoa korronte begizta gero eta txikiagoa eginez sortzen bada, baina korrontea eta azalera konstante mantenduz, eremuaren muga hurrengoa dugu:
Aurreko ataleko adierazpenetan ez bezala, muga hori zuzena da dipoloaren barne-eremurako.[15][14]
Dipolo magnetiko bat “Ipar poloa” eta “Hego poloa” pixkanaka elkarrengana hurbilduz sortzen da, beti ere; poloen karga eta distantziaren biderkadura konstante mantenduz. Lortutako muga eremua hurrengoa dugu:[15]
Eremu hauek formularen bidez daude erlazionatuta, non magnetizazioa den.
Momentu angeluarrarekiko erlazioa[aldatu | aldatu iturburu kodea]
Momentu magnetikoak lotura estua du efektu giromagnetikoa izeneko momentu angeluarrarekin. Efektu hau Einstein–de Haas deritzon efektuan adierazita dago maila makroskopikoan, “magnetizazio bidezko errotazioa”[16] delakoan, eta alderantziz, Barnett efektuan, “errotazio bidezko magnetizazioa” delakoan.
Dipolo magnetiko bat korronte-begizta gisa ikusteak argira ateratzen du momentu magnetikoaren eta momentu angeluarraren arteko lotura estua. Korrontea sortzen duten partikulek (begiztaren inguruan biraka egonik) karga eta masa dutenez, bai momentu magnetikoa bai momentu angeluarra handitu egiten dira errotazioa aldatzerakoan. Korrontea sortzen duten partikulek (begiztaren inguruan biraka) karga eta masa dutenez, bai momentu magnetikoa bai momentu angeluarra handitu egiten dira errotazio-tasarekin. Bien arteko erlazioari erlazio giromagnetikoa deritzo, , hau da,[17][18]
,
non L momentu magnetikoa eragiten duen partikularen (ala partikulen) momentu angeluarra den.
Korronte makroskopikoetan aplikatzen den Ampere-begiztaren ereduan, erlazio giromagnetikoa karga-masa erlazioaren erdia da. Mugimenduan dagoen eta karga duen partikula baten momentu angeluarra honela definitzen da:
,
non partikularen masa den eta v partikularen abiadura.
Beraz, korronte bat sortzen duten partikula kargatuen multzoak sortutako momentu angeluarraren adierazpena hurrengoa da:
,
non ρ mugimenduan dagoen partikularen dentsitatea den. Hitzarmenez, biderketa bektorialaren noranzkoa eskuin-eskuaren arauaren[19] bitartez ezartzen da.
Halaber, korronte hori osatzen duten partikula kargatuen kopuruak sortutako momentu magnetikoaren adierazpena da:
,
izanik eta mugimenduan dauden partikulen karga dentsitatea.
Hortaz, aurreko bi ekuazioak erlazionatuz:
,
e partikularen karga eta μ partikularen masa izanik.
Nahiz eta partikulak ezin diren zehaztasunez deskribatu karga-masa erlazio uniformearen karga orbitatuaren (eta birakariaren) banaketa gisa, eredu atomikoan g-faktorearen (partikularen eta konfigurazioaren araberakoa dena eta adimentsionala dena) bitartez adiraz daiteke:
Adibidez, nukleo baten inguruan orbitatzen duen elektroi baten momentu magnetikoaren g faktorea 1 da. Aldiz, elektroiaren momentu angeluar intrintsekoaren (spin) ondoriozko momentu magnetikoaren g faktorea 2 baino apur bat handiagoa da. Atomoen eta molekulen g faktorea elektroien momentu orbital eta intrintsekoek eragiten dute, eta, agian, baita nukleoen momentu intrintsekoek ere.
Atomo, molekula eta partikula elementalak[aldatu | aldatu iturburu kodea]
Funtsean, edozein sistemaren momentu magnetikoari egiten zaizkion ekarpenak bi motatako iturrietatik etor daitezke: karga elektrikoen mugimendutik, korronte elektrikoak bezala, eta oinarrizko partikulen magnetismo intrintsekotik, hala nola elektroia.
Lehenengo motako iturriei dagozkien ekarpenak kalkulatzeko, sistemaren barruko korronte elektriko guztien banaketa ezagutu behar da behean ageri diren formulak erabiliz. Bestalde, oinarrizko partikula bakoitzaren momentu magnetiko intrintsekoaren magnitudea zenbaki finko bat da, askotan zehaztasun handiz esperimentalki neurtzen dena. Adibidez, edozein elektroiren momentu magnetikoa −9.284764×10−24 J/T[20] da. Oinarrizko edozein partikularen momentu magnetikoaren norabidea guztiz zehaztuta dago bere spinaren norabideagatik eta balio negatiboa izateak edozein elektroiren momentu magnetikoa bere spinarekiko antiparaleloa dela adierazten du.
Edozein sistemaren momentu magnetiko totala iturri mota baten edo biren ekarpenaren batura bektoriala da. Esaterako, hidrogeno-1 atomoaren (hidrogenoaren isotopo azkarrena, protoi batez eta elektroi batez osatua) momentu magnetikoa hurrengo ekarpenen batura bektoriala da:
- elektroiaren momentu intrintsekoa,
- elektroiak protoiaren inguruan egiten duen mugimendu orbitala,
- protoiaren momentu intrintsekoa.
Era berean, barra-iman baten momentu magnetikoa momentu magnetiko eragileen batura da, non imanaren materialarekin parekatu gabeko elektroien momentu magnetiko intrintsekoa eta orbitala eta momentu magnetiko nuklearra kontuan hartzen diren.
Atomo baten momentu magnetikoa[aldatu | aldatu iturburu kodea]
Atomo batentzat, elektroi bakoitzaren spinak gehitu egiten dira spin oso bat lortzeko, eta momentu angeluar orbitalak ere gehitu egiten dira momentu angeluar orbital osoa lortzeko. Bi hauek momentu angeluarren akoplamendua erabiliz batzen dira, momentu angeluar osoa (totala) eratzeko. Momentu magnetiko nuklearrik gabeko atomo batentzat, momentu dipolar magnetikoaren magnitudea, , hurrengoa da:[21]
non momentu angeluar osoaren zenbaki kuantikoa, Landé-ren g faktorea, eta Bohr-en magnetoia diren. Momentu magnetiko honen osagaia eremu magnetikoaren norabidearen zehar hurrengoa da: [22]
m zenbaki osoa (ez nahastu momentuarekin) zenbaki kuantiko magnetikoa edo zenbaki kuantiko ekuatoriala da, eta edozein balio har ditzake:[23]
non faktore giromagnetikoa, m momentu magnetikoa, λ indargetze faktorea eta eremu magnetiko eraginkorra (kanpo-eremu magnetikoa gehi autoinduzitutako edozein eremu) diren. Lehengo terminoak momentuak eremu eraginkorraren gainean eragiten duen presezioa deskribatzen du; bigarrena, berriz, termino indargetzailea da non ingurunearekiko elkarrekintzaren ondorioz ematen den energiaren disipazioa adierazten du.
Elektroi baten momentu magnetikoa[aldatu | aldatu iturburu kodea]
Elektroiek eta oinarrizko partikula askok ere momentu magnetiko intrintsekoak dituzte, eta horien azalpenak tratamendu mekaniko kuantikoa eskatzen du, partikulen momentu angeluar intrintsekoarekin erlazionatzen dena, elektroien momentu magnetiko artikuluan eztabaidatzen den bezala. Momentu magnetiko intrintseko horiek eragiten dituzte magnetismoaren efektu makroskopikoak eta beste fenomeno batzuk, hala nola elektroien erresonantzia paramagnetikoa.
Elektroiaren momentu magnetikoa da:
,
non μB Bohren magnetoia, S elektroiaren spina eta g-faktorea, gS , 2 den Dirac-ek teoriaren arabera; hala ere, efektu elektrodinamiko kuantikoak direla eta, errealitatean 2 baino handixeagoa da: 2.00231930436. 2-ren desbideratze horri momentu dipolo magnetiko anomaloa deritzo.
Beste behin ere, garrantzitsua da ohartzea m spina biderkatzen duen konstante negatiboa dela eta, beraz, elektroiaren momentu magnetikoa spinarekiko paraleloa dela. Irudi klasiko honekin uler daiteke hori: biraketaren bultzada angeluarra ardatz baten inguruan biratzen den elektroi-masak sortzen duela imajinatzen badugu, biraketa horrek sortzen duen korronte elektrikoa kontrako norabidean mugitzen da, elektroiaren karga negatiboaren eraginez; korronte begizta horiek biraketaren kontrako momentu magnetikoa sortzen dute, hain zuzen. Beraz, positroi baten kasuan (elektroiaren antipartikula), momentu magnetikoa haren biraketarekiko paraleloa da.
Nukleo baten momentu magnetikoa[aldatu | aldatu iturburu kodea]
Nukleoa nukleoi, protoi eta neutroiz osatutako sistema fisiko konplexua da. Nukleoen propietate kuantikoen artean biraketak garrantzi handia dauka. Izan ere, nukleo baten momentu elektromagnetiko osoa nukleo partikularren errotazioaren menpekoa da.
Normalean nukleoak oinarrizko egoeran aurkitzen dira, baina, isotopo batzuen kasuan, kitzikatutako egoeretan egon ahal dira denbora luzez. Energia egoera bakoitza momentu dipolar baten bidez definitzen da.
Molekula baten momentu magnetikoa[aldatu | aldatu iturburu kodea]
Molekula guztien momentu magnetikoa ondo finkatuta dago, energia egoeraren araberakoa izanik. Molekula baten momentu magnetiko orokorra hurrengo gaien ekarpenez osatzen da:
- Parekatuta ez dauden spinen momentu magnetikoak (ekarpen paramagnetikoa), hauek existitzen diren kasuetan.
- Elektroien higidura orbitalari dagokion momentu magnetikoa (ekarpen diamagnetikoa). Balio hau oinarrizko egoeran kanpo eremu magnetikoaren proportzionala da.
- Nukleoaren errotazioaren ondoriozko momentu magnetikoa.
Erreferentziak[aldatu | aldatu iturburu kodea]
- ↑ Cullity, B. D.. (2009). Introduction to magnetic materials. (2nd ed. argitaraldia) IEEE/Wiley ISBN 978-0-470-38632-3. PMC 352837329. (Noiz kontsultatua: 2022-11-22).
- ↑ Callen, Herbert B.. (1985). Thermodynamics and an introduction to thermostatistics. (2nd ed. argitaraldia) Wiley ISBN 0-471-86256-8. PMC 11916089. (Noiz kontsultatua: 2022-11-22).
- ↑ IEEE Magnetics.. (Retrieved 19 February 2016.). "Magnetic units".. .
- ↑ Mohr, Peter J.; Newell, David B.; Taylor, Barry N.. (2016-09-26). «CODATA recommended values of the fundamental physical constants: 2014» Reviews of Modern Physics 88 (3): 035009. doi:. (Noiz kontsultatua: 2022-11-22).
- ↑ Le Système international d’unités [The International System of Units] (PDF) (in French and English) (9th ed.), International Bureau of Weights and Measures,2019. , 20-21 or. ISBN 978-92-822-2272-0..
- ↑ Le Système international d’unités [The International System of Units] (PDF) (in French and English) (9th ed.), International Bureau of Weights and Measures, 2019. , 23 or. ISBN 978-92-822-2272-0..
- ↑ a b c Magnetostatic Principles in Ferromagnetism. North-Holland.
- ↑ Griffiths, David J.. (1999). Introduction to electrodynamics. (3rd ed. argitaraldia) Prentice Hall ISBN 0-13-805326-X. PMC 40251748. (Noiz kontsultatua: 2022-11-22).
- ↑ Griffiths, David J.. (1999). Introduction to electrodynamics. (3rd ed. argitaraldia) Prentice Hall ISBN 0-13-805326-X. PMC 40251748. (Noiz kontsultatua: 2022-11-10).
- ↑ (Ingelesez) Boyer, Timothy H.. (1988-08). «The force on a magnetic dipole» American Journal of Physics 56 (8): 688–692. doi:. ISSN 0002-9505. (Noiz kontsultatua: 2022-11-10).
- ↑ Landau, L. D.. (1984). Electrodynamics of continuous media. (2nd ed., rev. and enl.. argitaraldia) Butterworth-Heinemann ISBN 0-7506-2634-8. PMC 33324186. (Noiz kontsultatua: 2022-11-10).
- ↑ Furlani, Edward P.. (2001). Permanent magnet and electromechanical devices : materials, analysis, and applications. Academic ISBN 978-0-12-269951-1. PMC 162129430. (Noiz kontsultatua: 2022-10-27).
- ↑ a b (Ingelesez) Yung, Kar W.; Landecker, Peter B.; Villani, Daniel D.. (1998). «An Analytic Solution for the Force Between Two Magnetic Dipoles» Magnetic and Electrical Separation 9 (1): 39–52. doi:. ISSN 1055-6915. (Noiz kontsultatua: 2022-10-27).
- ↑ a b Jackson, John David. (1975). Classical electrodynamics. (2d ed. argitaraldia) Wiley ISBN 0-471-43132-X. PMC 1288487. (Noiz kontsultatua: 2022-11-03).
- ↑ a b c Fuller., Brown, William. (1962). Magnetostatic Principles in Ferromagnetism. North-Holland PMC 456437027. (Noiz kontsultatua: 2022-11-03).
- ↑ Cullity, B. D.. (2009). Introduction to magnetic materials. (2nd ed. argitaraldia) IEEE/Wiley ISBN 978-0-470-38632-3. PMC 352837329. (Noiz kontsultatua: 2022-11-10).
- ↑ Krey, Uwe. (2007). Basic theoretical physics : a concise overview. (1st ed. argitaraldia) Springer ISBN 978-3-540-36805-2. PMC 191453107. (Noiz kontsultatua: 2022-11-10).
- ↑ Buxton, Richard B.. (2002). Introduction to functional magnetic resonance imaging : principles and techniques. Cambridge University Press ISBN 0-521-58113-3. PMC 45166697. (Noiz kontsultatua: 2022-11-10).
- ↑ Feynman, Richard P.. (©1963-1965). The Feynman lectures on physics. Addison-Wesley Pub. Co ISBN 0-201-02010-6. PMC 531535. (Noiz kontsultatua: 2022-11-10).
- ↑ «CODATA Value: electron magnetic moment» physics.nist.gov (Noiz kontsultatua: 2022-11-10).
- ↑ Tilley, R. J. D.. (2004). Understanding solids : the science of materials. J. Wiley ISBN 0-470-85275-5. PMC 54543926. (Noiz kontsultatua: 2022-11-22).
- ↑ Tipler, Paul Allen. (2003). Modern physics.. (4th ed.. argitaraldia) W.H. Freeman ISBN 0-7167-4345-0. PMC 49894577. (Noiz kontsultatua: 2022-11-22).
- ↑ Crowther, J.A.. (1949). Ions, Electrons, and Ionizing Radiations (8th ed.). London: Edward Arnold., 270 or..
- ↑ Advances in chemical physics. Volume 128. Wiley 2004 ISBN 0-471-48424-5. PMC 560025910. (Noiz kontsultatua: 2022-11-22).
- ↑ Micromagnetism and electrical resistance of ferromagnetic electrodes for spin injection devices. (1. Aufl. argitaraldia) 2004 ISBN 978-3-86537-176-8. PMC 76509368. (Noiz kontsultatua: 2022-11-22).
Ikus, gainera[aldatu | aldatu iturburu kodea]
- Momentu magnetiko nuklear
- Magnetismo
- Curie tenperatura (Momentu magnetikoak atala)
- Neutroi (Momentu magnetikoa atala)
- Trantsizio hiperfin
- Diamagnetismo
- Spin
- Erresonantzia magnetiko bidezko irudigintza
- Otto Stern





























































![{\displaystyle \mathbf {B} (\mathbf {r} )={\frac {\mu _{0}}{4\pi }}\left[{\frac {3\mathbf {\hat {r}} (\mathbf {\hat {r}} \cdot \mathbf {m} )-\mathbf {m} }{|\mathbf {r} |^{3}}}+{\frac {8\pi }{3}}\mathbf {m} \delta (\mathbf {r} )\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b47f91d20595386326b2945ac17533fd823321db)
![{\displaystyle \mathbf {H} (\mathbf {r} )={\frac {1}{4\pi }}\left[{\frac {3\mathbf {\hat {r}} (\mathbf {\hat {r}} \cdot \mathbf {m} )-\mathbf {m} }{|\mathbf {r} |^{3}}}-{\frac {4\pi }{3}}\mathbf {m} \delta (\mathbf {r} )\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1b635de5e52b7fd68571a72866d50392b0b7213)























