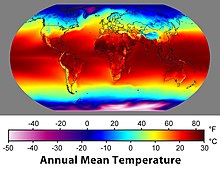
Tenperatura
Tenperatura magnitude fisiko bat da, termometroen bidez neurtzen dena; zehatzago deiturik, tenperatura termodinamikoa deritzo. Eguneroko bizimodu arruntean, tenperatura giza gorputzaren eta ingurumenaren arteko trasferentzia termikoa adierazten duten hotz- eta bero-sentsazioekin erlazionaturik dago.[1]
Tenperatura termodinamikoa Nazioarteko SI sistemako oinarrizko zazpi magnitude fisikoetako bat da, denbora, luzera, masa, korronte elektrikoa, materia-kantitatea eta argi-intentsitatearekin batera; gainerako magnitude fisikoak zazpi oinarrizko magnitue horietatik eratortzen dira. SI unitate-sisteman, tenperatura termodinamikoaren unitateari kelvin deritzo eta sinboloaz adierazten da.
Fisikan, zenbait modu desberdinetan definitzen da:
- Gasen teoria zinetikoan, materiaren oinarrizko osagaien agitazio termikoaren mailaren funtzio modura. Hain zuzen, gas idealen kasuan, energia zinaetikoaren balioa tenperaturaren proportzionala da.
- Sistema fisikoen arteko bero-transferentzien orekaren bidez.
- Entropia kontzeptutik abiaturik (termodinamikan eta fisika estatistikoan).
-
Proteina baten bibrazio termikoaren simulazioa. Bibrazioaren anplitudea handiagotu egiten da tenperatura igo ahala.
-
Gas baten tenperaturak bere barneko atomo eta molekulen higiduraren eta bibrazioen energiaren neurria adierazten du.
Termodinamikaren arloan, tenperatura garrantzi handiko propietate bat da; besteak beste, barne-energia eta entalpia kontzeptuetan agertzen da. Tenperatura propietate intentsiboa da, ez baitago sistemaren materia kantitatearen menpe; hau da, oreka termikoan dagoen sistema baten tenperaturaren balioa berbera da sistema osoa kontuan hartuta edo parte bat soilik kontsideraturik.
Fisikaren arloaz gain, tenperatura oso garrantzitsua da beste hainbat arlotan, hala nola meteorologian, klimatologian, medikuntzan eta kimikan, sukaldaritzan ere funtsezkoa dela ahantzi gabe.
Tenperatura termometroen bidez neurtzen da eta eskala ezberdinetan adierazi ohi da. Europan ohikoak diren termometro arruntetan, Celsius eskala erabiltzen da; bertako neurriak Celsius gradutan (gradu zentigradu ere esaten zaie) adierazten dira ( sinboloa). Eskala horretan izotza -an urtzen da, eta ura -an hasten da irakiten presio atmosferiko estandarrean (1 atm). Lurralde anglosaxoietan Fahrenheit eskala erabili ohi da, Fahrenheit graduak ( sinboloa) dituena bertan markaturik. Eskala horretan ura -an izozten da eta -an irakiten. Unitateen Nazioarteko SI sistemako unitatea kelvin izenekoa da eta sinboloaz adierazten da. Zero absolutuaren tenperatua da eta uraren puntu hirukoitzarena .
Tenperaturaren neurketaren historia[aldatu | aldatu iturburu kodea]
Termometria deritzo tenperaturaren neurketaz ari den fisikaren arloari.
Magnitude fisikoen artean, tenperatura zailenetakoa da zehazki neurtzeko, tartean bi arrazoi hauek baitaude:
- Batetik, oso ondo definitu behar da zein den tenperatura neurtu beharreko sistema. Horretarako, sistema horren propietate neurgarri erraz bat aukeratzen da.
- Tenperatura kontzeptuaren definizioa eta neurketarako erabilitako eskala ondo finkatzeko, bat ere intuitiboak ez diren zenbait kontzeptu termodinamiko ezagutu behar dira.

Hasieran, efektu ikusgai baten bitartez hasi zen tenperatura neurtzen: dilatazioa edo zabalkuntza; izan ere, berotzean, gorputzak dilatatu egiten dira, zabaldu.
Hasierako termoskopioak[aldatu | aldatu iturburu kodea]
Tenperatura-diferentziak detektatzeko tresna bat da termoskopioa, ondoren etorriko ziren termometroen aurrekaria. Termometroak ez bezala, termoskopioak ez zuen aukera ematen desberdintasun horiek modu absolutuan neurtzeko (datu kuantitatiboetan), modu erlatiboan baizik. Historikoki, ontzi bateko aire-kantitate jakin bat berotzean airearen bolumena handiagotu egiten zela nabarmentzeko gailua izan zen; eta txikiagotu egiten zela, ontzia hoztean.
Hain zuzen, 1612an, Paduako unibertsitako irakaslea eta Galileoren adiskidea zen Santorio Santorio medikuak alboko grafikoan ageri den bezalako termoskopio bat diseinatu zuen, gorputzaren tenperatura konstantea zela frogatzeko. Beirazko bola txiki bat zeukan, aire-kantitate konstante bat harrapatzen zuena, eta hodi ireki, luze eta estu bat gainditzen duela, urez betetako pitxer batean murgiltzen dena. Gaixoak bola eskuan edo ahoan jartzen du. Tenperaturaren eraginpean, airearen bolumen-aldaketak hodiko ur-zutabearen mailaren desplazamendua eragiten du. Santoriok bi erreferentzia-puntu finko erabiltzen zituen: elurraren eta kandela baten sugarraren tenperatura, eta horien artean graduazio uniforme hamartarra ezartzen zuen.

Geroago, zenbait hobekuntza egin ziren, beti ere airea-ura sistemak erabiliz.
Mota desberdinetako termometroak[aldatu | aldatu iturburu kodea]
Hurrengo mendean bestelako fluidoak hasi ziren erabiltzen, hala nola alkohol koloreztatuak (Réaumur) eta merkurioa (Fahrenheit eta Celsius). Horrela, termometro zehatzagoak prestatu ziren, tenperaturari balio numerikoa emateko bidea ahalbidetu zutenak.
Bide horretatik, 1730-1742 bitartean, Réaumur-ek (1683-1757) lehenengo alkohol-termometroa eraiki zuen 1730ean, eta Fahrenheit-ek 1736an eta Celsius-ek (1701-1744) 1742an merkurio-termometroak erabiliz, hainbat lurraldetan onartuak izan ziren tenperatura-eskalak proposatu zituzten.
Merkurio-termometroak[aldatu | aldatu iturburu kodea]
Daniel Gabriel Fahrenheit-ek (1686-1736) asmatu zuen merkurio-termometroa 1714. urte inguruan. Merkurio-termometroak behean merkurioz beterikoa arraboil edo anpulu bat du, goialdean diametro uniformeko beirazko hodi kapilar bat duena irekirik, bertara merkurioa iristeko moduan. Anpulua-hodia multzoa itxita dago, barneko airea eta likidoa irten ez daitezen; hau da, ontzi estankoa da, hermetikoa. Inguruko tenperatura igotzen denean, merkurioa dilatatu eta igo egiten da hodi kapilarrean gora; zenbat eta beroago, gorago. Hodiaren parean eskala bat marrazten da, tenperaturari balio numerikoa emateko.

Bestelako termometroak (elektrikoak)[aldatu | aldatu iturburu kodea]
Hemeretzigarren mendean zehar, lehenik 1821ean Seebeck efektua aurkitzean eta geroago efektu horretan oinarriturik termopareak asmatzean, 1888an platinozko erresistentziadun termometroa eraiki zen, tenperaturari balio elektrikoa esleitzean ahalbidetu zuena, eta horrela tenperaturari balioa analogikoa zein numerikoa eman ahal izan zitzaion (azken batean, voltmetro baten bitartez).
Termometro digitalak[aldatu | aldatu iturburu kodea]
Gaur egun, Europako hainbat lurraldetan baztertu egin dira merkurio-termometroak, merkurioaren toxikotasuna dela eta. Horien ordez, etxeetan ohikoak dira sukarra neurtzeko termometro digitalak. Horietan, pantaila batean agertzen da termometroaren muturreko sentsore txikian neurturiko tenperatura, Celsius gradutan emana.

Uhin elektromagnetiko infragorrien bidezko termometroak[aldatu | aldatu iturburu kodea]
Gorputz beltzean egindako lanen ondorioz, objektu batek igorritako argi-espektroaren analisian oinarritutako hirugarren gailu-sorta bat sortu zen. Neurtu beharreko sistema fisikoak gorputz beltzaren antzeko ezaugarriak dituela eta erradiazioaren transferentziak haren erradiazioa gehiegi asaldatzen ez duela suposatuz, behar bezala hautatutako bi tartetan energia-luminantzia neurtuz gero, haren tenperatura zehaztu daiteke. Hala, termometro infragorriak argiztapenean erabilitako kolore-tenperaturaren antzeko neurria hartzen du.
Tenperatura-eskalen historia[aldatu | aldatu iturburu kodea]
Termometroak asmatu zirenetik, zientzialariak tenperatura-eskalak zehazten saiatu ziren. Horretarako, egoera bateko tenperaturari zenbaki zehatz bat esleitu ahal izateko, bi egoera ongi definituren tenperatura finkoen arteko zabalkuntza hartu behar zuten erreferentziatzat, bata puntu “hotz” modura hartzeko, eta bestea puntu “bero” modura. Bi puntu horien tenperaturari balio numeriko bat esleitu zioten: zenbaki bana. Bi zenbaki horietan oinarriturik, tenperatura-eskalak asmatu ziren, jarraian aipatuko den moduan.


Erabilera arrunteko lehenengo tenperatura-eskalak[aldatu | aldatu iturburu kodea]
Puntu finko batetik besterako distantzia tamaina bereko segmentutan banatu zuten, erreferentziako bi puntuei esleitutako zenbakien arteko kendura kontuan izanik. Erreferentziako bi puntuen arteko segmentu bakoitzaren zegokion tenperatura-desberdintasunari “gradu” deitu zioten.
Hiru eskala nagusi sortu ziren XVIII.mendearen lehen erdialdean, Réaumur, Fahrenheit eta Celsius zientzialariek asmatuak. Horietako azken biak iritsi dira praktikan gure egunotaraino, eta horiek dira bizimodu arruntean erabiltzen ditugunak:
- Fahrenheit eskala: Gabriel Fahrenheit zientzialari alemaniarrak merkuriozko termometroa asmatu zuen 1720an, eta Fahrenheit eskala definitzeko erabili zuen, "Fahrenheit gradu" () izeneko ehun eta laurogei tarte dituena. Eskala horretan, uraren izozte-puntuari -ko tenperatura dagokio eta irakite-puntuari, -koa.
- Celsius eskala: Anders Celsius fisikari suediarrak Celsius eskala asmatu zuen 1741ean, "Celsius gradu" () izeneko ehun tarte dituena. Eskala horretan, da uraren izozte-puntuari dagokion tenperatura, eta da altuena, eta uraren irakite-puntuari dagokio.
- Reaumur eskala. René Antoine Ferchault de Réaumur (1683-1757) fisikari frantziarrak proposatu zuen 1731an. Reaumur eskalan laurogei "Reaumur gradu" daude uraren izozte puntuaren () eta irakite-puntuaren () artean.
Geroago, XIX. mendearen amaiera aldean, Lord Kelvin zientzialari britainiarrak eskala bat sortzeko ideia iradoki zuen. Kelvin eskala deitu ohi zaion eskala horretan, zero balioa eslaitzen zaio lor daitekeen tenperatura baxuenari, “zero absolutua” deritzonari. Fisikariek bazekiten -ko tenperaturan zegoela, eta, tenperatura horretara iritsitakoan, atomoak ezin zirela mugitu. Beraz, "zeroa" Celsius eskalako tenperaturan hartu zen. Konbentzio berri hori 1960an ofizialdu zen eta zehaztu zen.
Tenperatura termodinamikoaren definizioa[aldatu | aldatu iturburu kodea]
Ez da erraza tenperatura zer den zehaztea. Orain arte aipaturiko tenperatura-eskalak erabat alboratu gabe, kontzeptu termodinamikoetan oinarriturik egingo dugu zehaztapena, eta horregatik, hemendik aurrera tenperatura termodinamikoa deituko diogu. Magnitude fisikoa izanik neurtu beharrekoa denez, kontua da zer baldintzatan neur daitekeen, eta neurketan lorturiko emaitzari nola eslei dakiokeen balio numeriko bat.
Sistema fisiko baten barneko oreka termikoa[aldatu | aldatu iturburu kodea]
Tenperaturaren definizioa eman aurretik, oreka termikoa zer den ulertu behar da. Tamaina finituko sistema fisiko bateko eskualdeak tenperatura desberdinean egoten dira normalean. Horrelakoetan, esperientziak erakusten duenez, sistema bereko eskualdeen artean bero-transferentzia bat gertatzen da, eta, denbora pasatu ahala, eskualdeen arteko tenperatura-desberdintasunak gero eta txikiagoak izaten dira, harik eta une batean bero-transferentzia netorik ez dagoen arte. Une horretara iristean, sistema oreka termikora iritsi dela esaten da.
Termodinamikaren zero legearen bidezko definizioa[aldatu | aldatu iturburu kodea]
Termodinamikaren zero legeak dioenaren arabera, erabat bananduta dauden bi sistema fisiko beste hirugarren sistema batekin oreka termikoan badaude, lehenengo bi sistemak ere orekan daude beren artean. Definizio hau enpirikoa da, behaketa bidez atera baita teoriaz lortu ordez. Hiru sistemak oreka termikoan daudenez, hiruren propietate batek balio berbera du. Hain zuzen, sistema fisiko bat beste sistema batzuekin oreka termikoan dagoen ala ez zehazten duen propietate horri tenperatura deritzo.
Termodinamikaren bigarren legearen bidezko definizioa[aldatu | aldatu iturburu kodea]

Termodinamikaren bigarren legeak adierazten duenez, bestalde, ezinezkoa da bero-iturri bakar batekin beroa trukatu eta aldi berean berean lana egiten duen makina termiko bat eraikitzea. Lege horretan oinarriturik Carnot-ek (1796-1832) frogatu zuenez, tenperatura jakineko bi bero-iturriren artean egin daitezkeen ziklo termiko posibleen artean, Carnoten zikloa da lana lortzeko prozesurik eraginkorrena. Makina termikoaren eraginkortasun edo efizientzia honelaxe kalkula daiteke:
Entropia[aldatu | aldatu iturburu kodea]
Rudolf Clausius-ek (1822-1888) beroaren teoriari buruz eginiko lanean —1850ean argitaratua— termodinamikaren bigarren legeari buruzko ideia nagusiak sartu ondoren, 1865ean entropia kontzeptua sortu zuen. Entropia deritzon magnitudea ( sinboloa) sistema fisikoen propietate bat da, prozesu itzulgarri batean duen aldakuntza infinitesimala —— iturri batekin trukatutako beroa eta iturriaren tenperaturaren arteko zatidura modura definitzen dena:
Horretan oinarriturik, tenperatura termodinamikoa era berri batean defini daiteke, «prozesu itzulgarri batean trukatutako beroaren —— eta entropiaren aldakuntzaren —— arteko zatidura» gisa:
Alegia, tenperatura «prozesu itzulgarri bateko puntu bakoitzean trukatutako beroaren eta entropiaren aldaketaren arteko zatidura da».
Gaur egungo tenperatura-eskalak[aldatu | aldatu iturburu kodea]
Oro har, tenperatura-eskala definitzeko, propietate jakin baten menpe dagoen funtzio bat erabiltzen da: , zeinari "termometroaren tenperatura" deritzon. Tenperatura hori termometroarekin oreka termikoan dauden sistemen tenperatura da. Nolanahi ere, funtzio hori nahieran aukera daiteke. Aukera hori nolako den arabera, mota desberdinetako eskalak defini daitezke: eskala absolutua, eskala linealak...
Eskala absolutua[aldatu | aldatu iturburu kodea]
funtzioa propietatearen proportzionala izatea aukera daiteke:
Funtzioa zehazteko proportzinaltasun-konstantearen balioa finkatu behar da, puntu finko bat aukeratuz, erraz sor daitekeena. Hain zuzen ere, Parisen 1954ean egindako 10. Pisu eta Neurrien 10. Batzar Orokorrean, uraren puntu hirukoitza aukeratu zen puntu finkotzat. Egoera horretako tenperatura denez,
da, eta ondorioz:
non puntu hirukoitzaren egoerako propietate termikoaren balioa den. Kasu horretan, tenperatura nulua zero absolutuari dagokio. Horregatik esaten da eskala absolutua dela.
Eskala honetako unitate bakoitza kelvin bat da, SI sistemako tenperatura termodinamikoaren unitatea.
Eskala linealak[aldatu | aldatu iturburu kodea]
Tenperatura definitzeko funtzio modura erako funtzio lineala ere aukera daiteke. Orduan bi puntu behar dira funtzioa definitzeko. Adibidez,
- Celsius eskalan bi puntuak presio atmosferiko estandarreko uraren izozte-puntua eta irakite-puntua dira, eta horiei arbitrarioki eta balioak esleitzen zaizkie, hurrenez hurren. Kasu horretan, puntu horien tenperaturak (irakurtzean, "zero Celsius gradu") eta (irakurtzean, "zero Celsius gradu") dira.
- Fahrenheit eskalan ere, bi puntuak presio atmosferiko estandarreko uraren izozte-puntua eta irakite-puntua dira, baina horiei arbitrarioki eta balioak esleitzen zaizkie, hurrenez hurren. Ondorioz, puntu horien tenperaturak (irakurtzean, "hogeita hamabi Fahrenheti gradu") eta (irakurtzean, "berrehun eta hamabi Fahrenheit gradu") dira.
- Rankine eskala, eskala absolutuaren eta Fahrenheit eskalaren nahasketa bat da, baina unitate bakoitzaren kelvinaren balioa baino aldiz handiagoa izanik.
Tenperaturaren eskala termodinamikoa[aldatu | aldatu iturburu kodea]
Termodinamikaren bigarren legetik eratorria den Carnoten teoremak dioenaren arabera, bero-iturri berberen artean Carnoten zikloa osatzen duten bi makina itzulgarriren errendimenduak berdinak dira (eta maximoak). Beraz, errendimendua ez dago lan-substantzia edo propietateen menpe, bero-iturrien ezaugarrien menpe bakarrik egongo da. Bero-iturriak beren tenperaturagatik bereizten direnez, errendimendua bi tenperaturen funtzioa izango da soilik. Makinak eta tenperatura duten bero-iturrien artean lan egiten badu, errendimendua bi tenperatura horien menpe dago:
Orain, demagun hiru makina ditugula tenperatura desberdinetako hiru bero-iturriren artean lanean, non diren. Lehenengo makina eta bero-iturrien artean dabil, bigarrena eta iturrien artean eta hirugarrena eta iturrien artean, eta suposa dezagun bero-iturri bakoitzak bero-transferentzia berdina trukatzen duela berarekin aritzen diren beste bi makinekin. Hots, lehenengoak eta bigarrenak eman eta xurgatzen dute; bigarrenak eta hirugarrenak eman eta xurgatzen dute, hurrenez hurren; eta lehenengoak eta hirugarrenak ematen dute. Aurreko ekuazioa makina bakoitzari aplikatuz:
Kalkulu matematikoak eginez:
Lehenengo atala eta tenperaturen menpe soilik dagoenez, bigarren atalak ere horrela izan behar du, berdin dio zein den tenperatura. Hori horrela izan dadin, funtzioak honelakoa izan beha du:
Erlazio hori betetzen duten funtzioen arteko errazena Kelvinek proposatutakoa da:
Eskala guztiz definitzeko puntu bat finkatu behar da. Horretarako, uraren puntu hirukoitza kontuan hartuz, puntu horri tenperatura esleitzen zaio, eta orduan edozein punturen tenperaturaren balioa honelaxe definitzen da puntu hirukoitzaren tenperaturan oinarriturik:
non Carnoten makinak uraren puntu hirukoitzaren tenperaturan dagoen bero-iturriarekin trukatutako beroa den eta balioa Carnoten makinak tenperaturan dagoen iturriarekin trukatutako beroa.
Tenperatura-unitateak[aldatu | aldatu iturburu kodea]
Unitateen Nazioarteko SI sisteman, tenperatura termodinamikoaren unitatea kelvin izenekoa da, erabilera zientifikokoa eta zero absolututik () hasita zenbatzen dena, eta zeinaren graduazioa gradu zentigraduen ia berdina baita. Horrelaxe erabaki zuen Pisu eta Neurrien Batzar Orokorrak bere 10. bileran (1954), tenperaturaren oinarrizko puntu finkotzat uraren puntu hirukoitzarena hartuz eta, definizioz, puntu horri balioa esleituz. Geroago, 13. bileran (1967-68) «kelvin» izena (aurretik erabili ohi zen «Kelvin gradua» erabili ordez, eta letra xehez idatzia) eta «» sinboloa (lehenagoko «» erabili ordez) ere erabaki zituen, unitate honen erabilerari zegokionez. Zehazki, hauxe da orduan erabakitako definizioa:
«SI sisteman, tenperatura termodinamikoaren unitateak kelvin izenekoa da eta sinboloaz adierazten da. Definizioz, uraren puntu hirukoitzaren tenperatura termodinamikoari balioa esleitzen zaio, zehatz-mehatz.»
Geroago, 2018an SI sistemako oinarrizko unitateen berrazterketa egiten, unitate horien balioak aurretik zeuden bezala mantendu ziren; baina, etorkizunean etor daitezkeen aurrerapen teknologikoak kontuan harturik, unitate guztiak zazpi konstante unibertsalen bitartez definitu ziren.[2] Ondorioz honelaxe geratu zen kelvinaren definizioa:
«SI sisteman, tenperatura termodinamikoaren unitateak kelvin izenekoa da eta sinboloaz adierazten da. Beraren definizioa Boltzmann-en konstantearen biden dago zehaztuta, konstante horren balioa izanik; unitate hori unitateen baliokidea da, kilogramoa,metroa eta segundoa , eta konstante unibertsalen funtzioz definituta daudenean.»
Ikus daitekeenez, oso teknikoa da, eta ulertzeko zailagoa; baina, izatez, aurreko definiziokoaren balio berekoa.
Bestelako eskaletako unitateak[aldatu | aldatu iturburu kodea]
Gaur egun ere erabiltzen dira XVIII. mendean asmaturiko Celsius eta Fahrenheit eskalak, bizimodu arrunteko premietarako ohikoak baitira. Egin diren aldaketa bakarrak, eskala absolutuarekiko lotura zehazteko egindakoak dira.
- Celsius eskala
- Izatez, kelvin eskalaren ia berdina da, balio bakoitzari kenduta. Unitatea Celsius gradua deitzen da, eta sinboloaz adierazten da (letraren aurrean hutsarterik utzi gabe, gradua dela apimarratzeko). Izatez, Kelvin eskalaren translazio bat da. Bertan uraren puntu hirukoitzari dagokion tenperatura da.
- Eskala zentigradua edo eskala ehundarra ere deitzen da, bertan eta balioak finkoak baitira, presio atmosferiko estandarrean uraren izozte- eta irakite-puntuei dagozkienak
Fahrenheit eskala[aldatu | aldatu iturburu kodea]
- Unitatea Fahrenheit gradua deitzen da eta sinboloa da. Celsius eskalaren afina da, uraren izozte-puntua tenperaturan izanik eta irakite-puntua tenperaturan. Hortaz, 180 graduko tartea dago bi puntu horien artean, eta bi eskaletako graduen arteko erlazioa da.
Rankine eskala[aldatu | aldatu iturburu kodea]
- Eskala absolutuaren homotezia bat da, faktoreari dagokiona. Bertako gradu baten balioa kelvin baten balio bera da da.
Eskala desberdinetako tenperaturen arteko bihurketak[aldatu | aldatu iturburu kodea]
| Nondik abiatuta | Kelvin | Celsius | Fahrenheit | Rankine | Réaumur |
|---|---|---|---|---|---|
| . | |||||
Naturako tenperaturak[aldatu | aldatu iturburu kodea]
Naturan maila desberdinetako tenperaturak agertzen dira, eta materiaren zenbait propietate tenperatura desberdinetan gertatzen dira, ondoko taulan ikus daitekeenez.
| Tenperatura termodinamikoa () | Celsius tenperatura () | |
| Zero absolutua | ||
| Helio likidoa, He-3 isotopoa | ||
| Helio likidoa, He-4 isotopoa | ||
| Hidrogeno likidoa | ||
| Oxigeno likidoa | ||
| Nitrogeno likidoa | ||
| Uraren fusio-tenperatura presio estandarrean | ||
| Uraren puntu hirukoitzaren tenperatura | ||
| Lurrazaleko batez besteko tenperatura | ||
| Giza gorputzaren batez besteko tenperatura | ||
| Lurrazaleko airean erregistraturiko tenperatura altuena | ||
| Uraren irakite-tenperatura presio estandarrean | ||
| Urrearen urtze-puntua (fusio-tenperatura) | ||
| Titanioaren fusio-tenperatura | ||
| Eguzkiko gainazalean estimaturiko tenperatura |
Hutseko tenperatura[aldatu | aldatu iturburu kodea]
Tenperatura sistema fisikoen materiakon propietate bat da; hortaz, hutsean ez atomorik ez dagoenez, tenperatura ez dago definiturik bertan. Zerbait neurtzekotan, bertan jarritako termometro batek bere barne-energiari dagokion tenperaturaren balioa neurtuko luke. Dena den, gorputz guztiek energia kanporatzen dute etengabe erradiazio bidez, eta denbora pasatu ahala termometro horren tenperatura jaitsiz joango litzateke balio limite batera iritsi arte, zeina gorputzaren masaren araberakoa izango den. Baina, aldi berean, energia erradiatzearekin batera, bezala, gorputzak kanpotik datorkion erradiazioa ere xurga dezake, horrela tenperatura tenperatura igoz. Erradiazio bidez igorri eta xurgatutako beroak berdinak direnean, gorputza oreka termikoan egongo da.
Hutseko termometroa izar edo beste uhin elektromagnetikoen iturri nagusietatik isolatuta balego, hala ere, azkenean beraren tenperaturak balioko luke, hondoko erradiazio kosmikoa jasotzearen ondorioz, horixe izango bailitzateke oreka termikoatri dagokion tenperatura. Tenperatura horri espazioaren tenperatura deitu ohi zaio.
Eguratseko tenperatura eta sentsazio termikoa[aldatu | aldatu iturburu kodea]
Meteorologoek egunero ematen digute atmosferako tenperaturaren berri, eta oso kontuan hartzen ditugu haien eguraldi-aurreikuspenak. Baina aurreikuspen horietan, tenperaturaz gain bestelako faktoreak ere izaten ditugu kontuan; izan ere, faktore horiek garrantzitsuak dira gorputzean nabaritzen dugun bero- edo hotz-sentipena egituratzeko.
Sentsazio termikoa[3] deritzogu ingurumeneko baldintzen arabera giza gorputzak hautematen duen egoera edo erreakzioari. Argi eduki behar da sentsazio termikoa eta ingurumeneko tenperatura ez direla gauza bera. Bizimodu normalean, ohikoa izaten da “bero” edo “hotz” egiten duela esatea, beti ere termometroek markatzen duten tenperaturaren arabera. Baina, nolanahi ere, kontuan izan behar da termometroak adierazitako tenperaturak ez duela erabat determinatzen geure gorputzean hautematen dugun sentsazioa, zeren sentsazio termikoan tenperaturaz gain, beste zenbait parametrok ere eragiten baitute, eta horien arabera sentsazioa hobea edo txarragoa izan daiteke.
Oso konplexua da sentsazio termikoa neurtzea, baina, zer gertatzen den ulertzeko, gutxienez zenbait faktore eduki behar ditugu kontuan, besteak beste, honako hauek:
- Giza gorputzak autoerregulatu egiten du tenperatura, gutxi gorabehera konstante mantentzeko, inguruan. Horretarako, etengabe sortzen du beroa, jandako elikagaien digestiotik ateratako energiaren bidez. Inguruarekiko trukearen bitartez beroaren sorrera eta galera berdindurik edukitzean, ongizate termikoa lortzen da, eta eroso gaude, epel eta gustura. Beroaren galera sorrera baino handiagoa bada, “hotz” sentitzen dugu; galera txikiagoa bada, “bero”.
- Nolanahi ere, galera edo irabaziak ez daude soilik eguratseko tenperaturaren menpe, hortik aparteko beste zenbait faktoreren menpe baizik. Zeren inguruarekiko bero-trukea gertatzen baita konbekzioz (airea azalarekiko kontaktuan berotzean gorantz joanez eta alderantziz), kondukzioz (objektu beroagoen kontaktuan berotuz eta hotzagoekin hoztuz) eta erradiazioz (inguruko erradiazioa nolakoa den arabera), edo ebapotranspirazioz (izerdia edo mukosen edota azalaren hezetasuna baporatzean).
Horregatik, sentsazio termikoan lau motatako truke hauek hartu behar dira kontuan: tenperatura lehorra, tenperatura erradiatzailea, tenperatura hezea eta airearen abiadura.
Ikus, gainera[aldatu | aldatu iturburu kodea]
Erreferentziak[aldatu | aldatu iturburu kodea]
- ↑ Zientzia eta Teknologiaren Hiztegi Entziklopedikoa,. Elhuyar ISBN ISBN: 978-84-92457-00-7..
- ↑ (Frantsesez) (pdf) Le Système international d’unités (SI). .
- ↑ (Gaztelaniaz) Sensación térmica. .
Kanpo estekak[aldatu | aldatu iturburu kodea]
Bibliografia[aldatu | aldatu iturburu kodea]
- J.R. Etxebarria (arg.) (2003) Fisika orokorra (2. argitalpena), UEU. ISBN 9788484380450. Noiz kontsultatua: 2018-12-07
- M., Fishbane, Paul (2008) Fisika zientzialari eta ingeniarientzat. 1. bolumena, (1.etik-21.erako Gaiak) UPV/EHU. ISBN 9788490820308 Noiz kontsultatua: 2018-12-07.
- Marcelo Alonso, Edward J. Finn (1976), Física, Fondo Educativo Interamericano. ISBN 84-03-20234-
- Zientzia eta Teknologiaren Hiztegi Entziklopedikoa, Elhuyar, Donostia (2009). ISBN: 978-84-92457-00-7
| Tenperatura unitateak | ||
|---|---|---|
|
Kelvin • Celsius • Fahrenheit | ||