Zirkuluaren koadratura

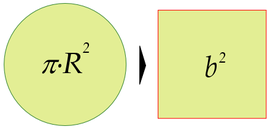
Zirkulua koadratu: irudiko karratuaren eta zirkuluaren azaleren balioa π da. 1882an frogatu zen irudi hori ezin dela urrats kopuru finitu batean lortu, konpasa eta erregela erabiliz.

Denbora luzean, itxurazko soluzio partzial batzuek itxaropen faltsuak eman zituzten. Irudi honetan, ilundutako figura lunula da. Haren azalera ABC triangeluaren azaleraren berdina da (Quios-eko Hipocrates-ek emandako emaitza).

Ez da existitzen zirkuluaren koadratura kalkulatzea baimentzen duen metodo geometrikorik, hau da, ezin dira azalera berdineko zirkulu bat eta karratu bat erlazionatu, erregela eta konpasa erabiliz soilik.

Zirkulua koadratzea antzinako matematikako hiru problema klasikoetako bat da. Problema geometriko hau, erregela eta konpasa bakarrik erabiliz, zirkulu baten azalera bera duen karratu bat lortzean datza. Problema geometriko hau eta zirkunferentzia bat zuzenki bihurtzea problema baliokideak dira. Bi problema hauek, era berean, π zenbakiaren eraikuntzarekin daude lotuta, unitate bateko luzera duen zuzenki batetik abiatuta.

π balioaren eraikuntza hau antzinako geometrek planteatu zuten, eta matematikariak  XIX. mendera arte saiatu ziren soluzioa aurkitzen, harik eta 1882an Carl Louis Ferdinand von Lindemann-ek ataza ezinezkoa zela frogatu zuen arte.

Matematikari honek frogatu zuen π balioa zenbaki transzendentea dela; eta ez aljebraikoa.  Bestela esanda, ez da koefiziente arrazionalak dituen polinomio baten erroa.

Zirkuluaren koadratura matematikako problemarik ezagunenetako bat da. Mendeetan zehar, matematikari profesional eta zaleek irtenbide bat bilatu zuten alferrik. Gaur egun, zirkulua koadratze kontzeptua metafora bihurtu da hizkuntza askotan, soluzio gabeko lan bat adierazteko.

Historia

Historiaurrea

Ahmesen hurbilketa metodoa ( Ahmesen papiroarena):  9 unitateko diametroko zirkulu bat 9 unitateko aldeak dituen lauki batean inskribatua dago. Lauki hori 3 unitateko aldeak dituzten 9 lauki txikiagoetan zatitzen da. Zirkuluaren  azalera, gutxi gorabehera, 7x9ko oktogono irregular bati dagokio; eta zehatzago, 8 unitateko aldea duen lauki bati

Ekialdeko hainbat kulturatan jadanik garatuta zituzten zirkuluen azaleren hurbilketak kalkulatzeko zenbait prozedura. Adibidez, Ahmesen Papiroan (K.a. 1650 urte inguruan) ikus daiteke zirkuluaren diametroa 9 zatitan banatua; hau da, metodo honen bidez kontsideratzen da zirkuluaren diametroaren neurria 9 unitatekoa dela, eta azalerarako formula aplikatuz, pi*r^2=pi*(9/2)^2=63,62… unitateko azalera duela lortzen da. Aipagarria da lortutako azaleraren hurbilketa hau 8 neurriko aldea duen karratu baten azaleraren antzekoa dela izan ere, karraturako azaleraren formula aplikatuz, A=a^2=8^2=64 lortzen da.

Bigarren metodo batean, zirkuluaren hurbilketa oktogono irregular baten bidez egiten da. Horretarako, 9x9 tamainako karratu bat hartzen da, eta horri 18 unitate kentzen zaizkio, triangelu berdintsuen bidezko mozketak eginez. Honela, geratzen den eremua 9x9-18=63 unitatekoa da.

Matematikan oinarritutako lehenengo arrazoibide deduktiboak, teoremen bidez argudiatutako froga matematikoak  erabiltzen zituztenak, K.a. VI. mendetik aurrera garatu ziren Grezian. Hein batean, Miletoko Talesen lanetan ikus daitezke, eta argiago Pitagorasek sortutako eskola pitogarikoan. Bi zenbaki errealen arteko  arrazoia zenbaki irrazionala  izan daitekeela frogatu zutenean matematikari pitagorikoek, erregela eta konpasez eraiki daitezkeen zenbait objektu (adibidez, karratu baten diagonala) zenbaki osoen zatidura gisa ezin daitezkeela irudikatu egiaztatu zuten. Aurkikuntza hori garrantzi handikoa bihurtu zen. Izan ere, ordura arte ezagutzen ziren zenbaki-mota bakarrak zenbaki osoak eta proportzio osoak ziren (gaur egungo terminologian, "zenbaki arrazionalak"). Ondorioz, pentsatu zen zuzen geometriko guztiek proportzio arrazionala izan behar zutela, hau da, luzera osoko erlazioa izan behar zutela elkarren artean. Beraz, pitagorikoek frogatu zuten aurreko kontzeptuen bitartez modu aritmetikoan adierazi ezin ziren "zenbakiak" modu geometrikoan eraiki zitezkeela luzeeren bidez (egungo terminologian, "zenbaki irrazionalak" dira).

Bat-batean, geometriak aritmetikak adieraz zezakeena baino gehiago irudika zezakeen. Aurkikuntza horren emaitza gisa, aritmetika bigarren plano batera pasatu zen geometriaren aldean. Une horretatik aurrera, ekuazioak geometrikoki ebatzi beharko ziren (adibidez, irudiak bata bestearen ondoan jarriz eta laukizuzen edo karratu bihurtuz). Matematika zaharrak planteatutako hiru problema klasikoak V. mendearen amaierakoak dira 8eta denak eraikitze-problemak ziren): zirkulua koadratzeaz gain, angeluaren trisekzioaren lana eta Delos-en problema (kubo bat bikoiztean datzana).

Oro har, hiru problema horiek planteatu zirenean, ez zen eskatzen eraikuntza-baliabideak erregelara eta konpasera mugatzea. Hasiera batetik aurkitu ziren laguntza osagarrietan oinarritutako soluzioak. Hala ere, denbora pasa ahala,  murrizketa zorrotzagoak ezartzeko joera sortu zen.

Lehen lanak

Plutarko idazle grekoaren arabera, Anaxagoras filosofoa izan zen zirkuluaren koadraturari buruz idatzi zuen lehenetarikoa, espetxean egon zen bitartean, baina ez du xehetasun gehiagorik ematen Anaxagorasen eraikuntzari buruz. Anaxagoras K.a.430 inguruan atxilotu zuten, asebeia leporatu ziotenean.

Ikerketa honen hasierai buruzko iturri zehatzenak Aristotelesen lanen gaineko iruzkinak dira, antzinaro berantiarrean idatzitakoak nagusiki. Hau da, 900 urte inguruko aldearekin idatzi ziren testuak. Ondorioz, lehen ikuspegien ordena kronologikoa eta pentsamendu-prozesuak zalantzazkoak dira.

“Hipocratesen lunulak”: lunula berdeen eta triangelu angeluzuzenaren azalerak baliokideak dira.

Triangeluak laukizuzen bihurtzea, laukizuzenak karratu bihurtzea (laukizuzenaren koadratura) edo bi karraturen batura (Pitagorasen teorema) ezagutzen ziren teorema geometrikoen oinarrizko praktikak ziren. K.a. 440. urtearen inguruan, Quiozeko Hipokratesek adibide bat eman zuen adieraziz nola eremu lerromakur bat zehazki karratu bihur zitekeen.

Zirkulu baten antzeko segmentuen eremuek beren soken gainean karratuek bezala jokatzen dutela dioen teoreman oinarrituta, Hipokratesek arku zirkularrek mugatutako eremuak koadratzea lortu zuen, "Hipokratesen lunula" deritzenak. Hala ere, zirkuluaren koadratura ezin da horrela lortu, zenbait lunula baino ezin baitira koadratu (adibidez, karratu baten aldeen gainean eraikitakoak koadratu daitzeke, baina ezin da egin hexagono erregular baten aldeetatik abiatuta).

XX. mendean, Txebotariov eta Dorodnovek frogatu zuten, oro har, lunulak ezin direla koadratu, Hipokratesek proposatutako hiru lunulak eta Leonhard Eulerrek XVIII. mendean gehitu zituen beste bi mota izan ezik. Modu honetan, argi geratu zen lunularen koadratura problema askaezin baten salbuespena besterik ez zela. Salbuespen horrek, ordea, mendeetan zehar, matematikariak nahasi egin zituen, lunulek zirkuluaren koadraturara hurbildu ahalko zituztela uste baitzuten.

Triangeluak (eta, beraz, poligonoak) karratu bihurtu ahal izatea izan zen zirkuluaren azalera bereko poligono bat eraikitzeko bigarren ikuspegia. Antifonteren ideia izan zen zirkulua poligono inskribatuekin hurbiltzea. Herakleako Brisonek prozedura hori hobetu zuen, zirkulua poligono zirkunskribatuekin hurbilduz eta tarteko balio bat eratuz.

Hipias Elidekoak K.a. 425. urtearen inguruan, angeluaren trisekzioa ebazteko prozedura bat asmatu zuen, mekanikoki sortutako eta  mugimendu zirkular bati gainjartzen zaion kurba lineal baten bidez. Ehun urte geroago, Dinostratok ikusi zuen Hipiasek erabilitako kurba horren laguntzarekin (Hipias koadratrizea deritzona) 2/π  luzerako segmentua eraiki daitekeela, eta oinarrizko eraikuntza gehiagoren laguntzarekin, π azalerako karratua halaber. Hala ere, zirkunferentzia kurba transzendentea denez, ezinezkoa da haren garapena erregela eta konpasarekin soilik lortzea, eta, beraz, ez zen lortu bilatzen zen soluzioa, zentzu hertsian, aurkitzea.

Arkimedes

Zirkuluaren koadratura espiralaren laguntzarekin: Izan bedi A puntua espiralak lehenengo itzulia (O jatorriaren inguruan) egitean lortzen den puntua. Espiralaren A puntuko ukitzaileak OA-rekiko perpendikularra den zuzena mozten du B-n. Arkimedesen arabera, BO zuzenkia eta OA erradioko zirkunferentzia berdinak dira; hortaz, zirkulu gorriaren azalera eta triangelu urdinaren azalera baliokideak dira.

"Neurketa zirkularra" izenburua duen tratatua iritsi zaigu Arkimedesengandik; bertan Arkimedesek oinarrizko hiru teorema frogatu zituen:

1. Zirkulu baten eta triangelu zuzen baten azalera berdinak izango dira, baldin eta triangelu zuzenaren katetoetako baten neurria zirkuluaren erradioa bada eta beste katetoa zirkulu horren perimetroaren luzera bada. Zirkuluaren azalera  honela kalkula daiteke: (½·erradioa·zirkunferentzia).
2. Zirkulu baten azalera eta bere diametroaren karratua erlazionatuta daude gutxi gorabehera π/4 arrazoiarekin.
3. Zirkulu baten zirkunferentzia bere diametroa bider (3+10/71) baino handiagoa da, eta diametroa bider (3+10/70) baino txikiagoa.

Lehenengo proposizioam oinarrituta, erradio jakin batetik abiatuta, zirkulua koadratzearen problema zirkulu horren zirkunferentziaren eraikigarritasunera mugatu zen eta, beraz, pi-rem eraikigarritasunera.

Hirugarren proposizioan, Arkimedesek zenbaki horren hurbilpen bakun eta zehatza eman zuen, 22/7 (≈ 3,143), gaur egun helburu praktikoekin erabiltzen dena. Bigarren proposizioa arestian aipatutako bi proposizioen korolario sinple bat da: zirkulu baten azalera bere diametroaren karratuarekiko proportzionala dela, Euklidesek bazekiena.

Arkimedesek hemen eman zuen proportzionaltasun-konstantearen balioa.

Haren baieztapenen froga gisa, Arkimedesek Herakleako Brisoneren ideia hartu zuen oinarri. Haren bidez zirkuluaren edozein hurbilketa lor daiteke inskribatutako eta zirkunskribatutako poligono erregularrak erabiliz. Inskribatutako hexagonotik eta zirkunskribatutako triangelutik abiatuta, Arkimedesek 96 alde zituen poligonoa garatu zuen, hurrenez hurren aurpegi kopurua bikoiztuz.

Liejako Francoren zirkuluaren koadratura, zirkulua 44 sektoretan banatuz, eta horrek elkartzen ditu laukizuzen bat osatzeko.

Liejako Franco izan zen zirkuluaren koadraturaren arazoa berrikusi zuen Erdi Aroko lehen autoreetako bat. Francok, 1050. urte inguruan, De quadratura circuli lana argitaratu zuen, eta bertan, lehen aldiz, koadraturaren hiru sistema aurkeztu zituen. Gero, ordea, Francok berak hiru sistema horiek ez zituen onartu. Lehenengo biak ziren, hurrenez hurren, zirkuluaren diametroa bider ⅞ aldeko karratua, eta zirkuluaren diametroa bider 10/8 distantziako diagonala zuen karratua. Bi hurbilketa hauek nahiko eskasak izan ziren; izan ere, π zenbakia 3 + 1/16 eta 3+ ⅛ balioetara hurbiltzen zuen. Hirugarren iradokizunak, berriz, karratuaren perimetroa zirkuluaren zirkunferentziarekin parekatzen du, azken hau zuzentzea behartzen duena.

Dena den, Francoren azken lana 14 unitateko diametroa duen zirkulu batean oinarritu zen, zeinari   7² x 22/7 = 154ko azalera zehazten zehaztu zion. Francoren argudiaketaren arabera, ezin da matematikoki aurkitu azalera hori duen  karraturik, 22/7ren erro karratua irrazionala baita; alabaina geometrikoki eraikigarria den eta neurri arrazionala ez duen zuzen neurrigabe beten bidez, 22/7ren erro karratuak bilatutako koadratura emango luke. Emaitza horretara iristeko, zirkulua 44 sektore berdinetan zatitu zuen, zeinak konbinaty zituen 11 eta 14 aldeko laukizuzena osatzeko. Hala ere, Francok ez du azaltzen zergatik ordezten dituen sektore zirkularrak 1 eta 7 luzerako katetodun triangelu angeluzuzenekin.  Deskonposizio egoki baten bidez laukizuzena karratu bihurtzeko ahalegina ere arazotsua da. Bistan denez, Franco ez zegoen ohituta greziarren prozedura tradizionalarekin.

Aro moderno hasierako aurrekuntzak

Aro modernoaren hasieran, zirkuluaren koadraturarako hurbilketa hobeak lortu ziren serie infinituak erabiliz, bereziki funtzio trigonometrikoak erabiltzen dituzten serie matematikoak hedatuz. ​​François Viètek  pi-ren lehen irudikapen zehatza aurkitu bazuen ere, hark proposatutako formula erabiltzeko latza zen. Biderketak eta zatiketak besterik behar ez duen serie sinpleagoa John Wallisetik lanetik dator, eta William Brounckerri zor zaio π kalkulatzeko beste formula bat, frakzio jarraitu baten bidezkoa.

Praktikan, denboran aurrera joan ahala, garrantzitsuagoa izango zen James Gregoryk eta Gottfried Leibnizek arku tangentea kalkulatzeko bakoitzak bere aldetik aurkitutako seriea. Serie horren konbergentzia mantsoa izan arren, serie hau erabiliz, π zenbakia kalkulatzeko oso egokiak diren beste serie batzuk ondoriozta daitezke. XVIII. mendearen hasieran, π-ren 100 digitu baino gehiago kalkulatu ziren serie horien laguntzarekin, baina ezin izan zen zirkuluaren koadraturaren arazoari buruzko ezagutza berririk lortu.

Ezintasuna

Zirkulua koadratzearen problema erregela eta konpasarekin ebazteak, ${\sqrt {\pi }}$ zenbakiaren eraikuntza eskatzen du. ${\sqrt {\pi }}$ zenbakia da, hain zuzen, 1 unitateko erradioko zirkulu baten azaleraren berdina duen karratu baten aldearen luzera. Eraikuntza egiteko, bi lerro zuzen, bi zirkunferentzia edo lerro zuzen eta zirkunferentzia bat zeharkatu behar dira puntu berriak lortzeko, urrats kopuru finitu batean.

${\sqrt {\pi }}$ zenbaki eraikigarria balitz, $\pi$ zenbakia, halaber, erregela eta konpasaren prozeduratik eratorria, eraikigarria izango litzateke. 1837an, Pierre Wantzel-ek frogatu zuen erregela eta konpasa erabiliz lortzen diren luzerak koefiziente arrazionaletako polinomioen zenbait ekuazioren soluzioak izan behar zirela. Hortaz, luzera eraikigarriak zenbaki aljebraikoak izan behar dira. Orduan, zirkuluaren koadratura erregela eta konpasarekin lortu baliteke, zenbakia aljebraikoa izango litzateke. Alabaina, Ferdinand von Lindemann-ek 1882. urtean frogatu zuen zenbakiaren traszendentzia (alegia, ez dela existitzen ekuazio aljebraikorik soluzio bezala duena), eraikuntzaren horren ezintasuna erakutsiz.

Problema honen ospea

Matematikako gaiekin gutxitan gertatzen bada ere, zirkuluaren koadraturak ospe handia lortu zuen matematikatik kanpo ere eta, beraz, matematikari amateur asko saiatu ziren itxuraz sinplea zirudien problema hau konpontzen. Are gehiago, beste batzuek konpondu zutela uste izan zuten.

Lindemannek 1882an problemaren ebazpen-ezintasun frogatu arren, XX. mendean zirkuluaren ustezko koadraturak argitaratu ziren oraindik. Azken urteetan, matematikaren zaleek problema ebatzi nahian egindako huts-egiteak jolas-matematikaren beste gai bat bihurtu dira.

Zirkuluaren koadratura ospetsuak

Zirkuluaren koadratura aurkitu zuela uste zuen matematikari amateur baten adibide nabarmena Thomas Hobbes filosofo ingelesa izan zen. Ustezko soluzioa 1665eko De corpore lanean argitaratu zuen, eta urte horretan bertan ezeztatu zuen John Wallisek. Izatez, gutxi gorabeherako eraikuntza hurbildua baino ez zen.

Lambertek (1728-1777) zirkuluaren gutxi gorabeherako hiru koadratura aipatzen ditu, hirurak zenbait balio arrazionalen bidez lortuak. Lan horiek, XVIII. mendearen erdialdean argitaratuak, 35/31 zatikian oinarritzen dira, eta zirkuluaren diametroaren eta azalera bereko karratuaren aldearen arteko erlaziorako balio dute. Lambertek egin zuen lan hori $\pi$ zenbakiaren hurbilketa hau ematen du:

$\pi \approx {\frac {3844}{1225}}=3{,}1{\color {red}379\ldots }$

Edward J. Goodwin mediku estatubatuarraren koadratura American Mathematical Monthly aldizkariaren lehen liburukian agertu ere egin zen 1894an, baina autorearen iragarki gisa baino ez. Lana bera kontraesanetan sartzen da eta, irakurketa nola interpretatzen den arabera, $\pi$-ren balio desberdinak sortzen ditu.

Artea eta kultura

"Koadratura zirkular" edo "koadratzaile" baten agerpenaren ebidentzia goiztiar gisa, Aristofanesen Txoriak komediaren pasarte bat aipatu ohi da, K.a. V. mendekoa. Bertan, Meton pertsonaia topografo-lanetan agertzen da, hiri berri baten planoan lan egiten duena, eta laguntza geometrikoen bidez "zirkulua karratu bihurtu" nahi du. Hala ere, esaldi hori ez da zirkulu baten koadraturaren aipamena, baizik eta elkarrekin angelu zuzenak eratuz gurutzatzen diren bi kaleren sorrera, nahiz eta adierazpen horrek zirkuluaren koadraturaren aipamena dirudien.

1321ean, Dante Alighierik, Jainkotiar komedia lanean, zirkuluaren koadratura giza ulermenetik haratago doan atazatzat zuen, paradisua ulertzeko bere ezintasunarekin konparatzen zuena.

1922an argitaratutako James Joyceren nobela berritzailean, Ulises, kontatzen da 1882ko udan Leopold Bloom protagonistak gogor jardun zuela "zirkulua koadratzeko" arazoari irtenbidea emateko, dirutza handia lortzeko asmoz. Eleberriaren amaieran, bere aitarekin izandako elkarrizketa luze batean, triste eta desengainatuta, Bloomek bere porrota onartzen du.

Eraikuntza hurbilduak

Dureroren araberako prozedura babilonikoa (1525)

Konpas eta erregela erabilita soluzio zehatzik lortu ezin bada ere, badira zirkuluaren koadraturarako gutxi gorabeherako eraikuntzak edo eraikuntza hurbilduak, helburu askotarako behar bezain zehatzak direnak.

Metodo sinpleak, antzinatik ezagunak, zirkuluaren diametroa edo erradioaren eta karratuaren alde edo diagonalen arteko erlazio osoa adierazten dute. 8 unitateko diametroko zirkuluaren eta 10 unitateko diagonaleko karratuaren arteko ekuazioa aurkitu daiteke bai babiloniarretan bai Vitruvio erromatar lur-neurtzailearen argitalpenetan. Alberto Durero-k marrazteko era egokia eskaintzeko, eraikuntza hori berreskuratu zuen 1525. urtean bere Vnderweysung der messung mit dem zirckel und richtscheyt lanean.

Kochański-ren eraikuntza

Kochańskiren eraikuntza hurbildua (1685)

Adam Adamandy Kochański matematikari poloniarrak 1685ean zirkulu baten zirkunferentzierdirako soluzio hurbildu bat aurkitu zuen. Prozedura osoa konpasaren irekiera berarekin egiten da. Erakutsitako eraikuntzak aukera ematen du zirkunferentzierdiaren errektifikazioa lortzeko, alegia, zirkunferentzierdiaren luzera duen zuzenki lortzeko. Emandako $r$ erradiotik abiatuta, Kochańskik gutxi gorabehera $r\cdot \pi$ luzerako lerro zuzen bat eraiki zuen, zirkunferentziaren erdiaren luzera zeukana. Alboko irudian gorriz marraztutako laukizuzenak, beraz, zirkuluaren ia azalera bera du, ${\overline {AZ}}\cdot r\approx r\cdot \pi ^{2}$. Koadratura hurbildua lehenengo emaitzatik eta triangelu angeluzuzenen legeetatik eratorria da, azken hauek laukizuzenaren koadratura lortzea ahalbidetzen baitute. Eraikuntza hau $\pi$ lau hamartarrekin hurbiltzen du:

$\pi =3{,}141\;592\ldots \approx {\overline {AZ}}=r\cdot {\sqrt {(3-\tan 30^{\circ })^{2}+4\,}}\ \approx \ 3{,}141\;5{\color {red}33}\cdot r$

Erroreen tamaina erakusteko adibideak:

r = 100 metroko duen zirkulu batentzat, lortutako karratuaren aldearen luzeeraren errorea -1,7mm-koa da gutxi gorabehera.

r = 1 m duen zirkulu batentzat, azaleraren errorea -59 mm²-koa da.

Jacob de Gelder-en eraikuntza

Jacob de Gelder garatutako eraikuntza, koadratura gehigarriarekin (lerro ez-jarraituak)

1849an (S. A. Ramanujanen Construction agertu baino 64 urte lehenago), Jacob de Gelder (1765-1848) matematikari herbeheretarrak asmatutako eraikuntza sinple eta dotorea argitaratu zen Grünert-eko Artxiboan. De Gelderren eraikuntza hurrengo hurbilketan oinarrituta dago:

$\pi \approx {\frac {355}{113}}=3,1415929\ldots$

Balioa bi batugaitan zatituz:

$3+0,1415929\ldots$

Zatiki hori Zu Chongzhi-ren zatikia izenez ezagutzen da, izen bereko V. mendeko matematikari txinatar horrek aurkitu baitzuen. Ikus daitekeenez, bere lehen sei hamartarrak balioaren lehen sei hamartarrekin bat datoz.

Horregatik, Jacob de Gelderrek ez zuen laukiaren aldea eraiki, hurrengo balio aurkitzearekin nahiko izan zuen:

${\overline {AH}}={\frac {4^{2}}{7^{2}+8^{2}}}=0,1415929\ldots$

Ondoko irudia, jarraian deskribatuko dena, Jacob de Gelderren eraikuntza erakusten du.

Prozedura hurrengoa da: ${\overline {CD}}=1$ duen erradioko zirkulu baten bi diametro perpendikular marraztu eta A eta B ebakidura puntuak zehaztu. ${\overline {CE}}={\frac {7}{8}}$ zuzena marraztu eta E A-rekin lotu. A-tik hasten den ${\overline {AF}}={\frac {1}{2}}$ zuzena zehaztu ${\overline {AE}}$-n. ${\overline {CD}}$-ren paraleloa den ${\overline {FG}}$ segmentua marraztu eta E G-rekin lotu. ${\overline {FH}}$ segmentua marraztu, ${\overline {EG}}$-rekin paraleloa, ${\overline {AH}}={\frac {4^{2}}{7^{2}+8^{2}}}$ izatea lortuz. ${\overline {BJ}}={\overline {CB}}$ jarri, eta, ondoren, ${\overline {JK}}={\overline {AH}}$. ${\overline {AK}}$ bitan zatitu, L lortuz, eta A-n hasita L-tik Thales-en zirkulua marraztu. Horrek M ebaki puntua emango du. ${\overline {BM}}$ zuzena ${\overline {AK}}$-ren erro karratua da eta, beraz, bilatutako karratuaren aldearen luzera.

Erroreen tamaina erakusteko adibideak:

r = 100 km-ko erradioa duen zirkulu batentzat, lortutako karratuaren aldearen luzeraren errorea 7,5 mm-koa izango litzateke.

r = 1 m-ko erradioa duen zirkulu batentzat, arearen errorea  0,3 mm²-koa izango litzateke, gutxi gorabehera.

Hobson-en eraikuntza

1913. urtean E. W. Hobson matematikari britaniarrak aurkitu zuen eraikuntza sinple eta ulertzeko erraza. Hiru arkuz eta angeluzuzenean jarritako bi segmentuz baliatuta, nahikoa izan zuen karratuaren aldea zehazteko.

Alboko irudiak erakusten du Hobson-en eraikuntza: nola zirkulutik hasita karratua lortu zuen. Prozedura:

• $AOB$ diametroko zirkunferentzia marraztu.
• ${\overline {OD}}={\frac {3}{5}}\cdot r$, ${\overline {OF}}={\frac {3}{2}}\cdot r$ eta ${\overline {OE}}={\frac {1}{2}}\cdot r$ zuzenak zehaztu.

${\overline {DE}}$ eta ${\overline {AF}}$ diametroko $DGE$ eta $AHF$ zirkunferentziak marraztu, hurrenez hurren. Azkenik, ${\overline {AB}}$-tik $O$-rako zuzen perpendikularra marratu. Horrela, $G$ eta $H$ ebaki puntuak lotzean $\pi$-rekin erlazionatuta dagoen karratuaren aldea lortzen da.

${\overline {GH}}=r\cdot 1{,}772\;4{\color {red}67\ldots }$

$r=1$ erradioko zirkulu batentzat, karratuaren aldearen luzeraren lehen lau hamartarrak ${\sqrt {\pi }}=1{,}722\;453$ balioarenekin bat datoz.

Erroreen tamaina erakusteko adibideak:

r = 100 m erradioko zirkunferentzia batentzat, karratuaren aldearen luzeraren errorea 1,4 mm-koa izango litzateke.

r = 1 m erradioko zirkunferentzia batentzat, karratuaren arearen errorea 46 mm²-koa izango litzateke.

Gutxi gorabeherako emaitza zatiki bat erabiliz

$\pi$ baliora hurbiltzen den zatikia aurkitzen bada, Tales-en hirugarren teorema erabilita, erregela eta konpasarekin -ren nahi adina hamartar eraiki daitezke. Zirkulu baten arearen berdina duen karratu baten aldearen luzera zehazteko, hurrengo zatikiaz baliatuko gara:

${\frac {245850922}{78256779}}=3{,}141\;592\;653\;589\;793{\color {red}\;160\;\ldots }$

Zatiki horrek, -ren hurbilketa gisa, hamabost leku hamartar zehatz ematen ditu. Frakzio horren alderantzizkoa Johann Heinrich Lambert-ek aurkitu zuen 1770. urtean.

Kanpo estekak

• Datuak: Q193394
• Multimedia: Squaring the circle / Q193394