Simetria
Simetria da propietate bat
objektu batena berez
itxura bera baldin badauka
begiratuta aldrebes
karratu eta zirkuluetan
nahiz ikus liteken errez
Simetrikoa da banatuta
erdiko komaren bidez
“Orea ore, eroa ero”
esaldia adibidez.

Simetria kontzeptua (συμμετρεῖν grezieratik, elkarrekin neurtu) forma geometriko, sistema, ekuazio eta beste objektu material edo abstraktu batzuen ezaugarri berezi bat da, transformazio, mugimendu eta aldaketetan oinarritzen dena[1][2].
Definizio hain zabala adibide honekin ikus daiteke erraz: demagun ispilu baten aurrean gaudela oinak eta besoak luzatuta. Laster ikusiko dugu gure gorputzaren ezkerreko eta eskuineko aldeak (lehen begiratuan behintzat) berdinak direla. Adibide hori aldebiko simetria deritzona da. Kasu horretan, objektua gure gorputza izango litzateke, eta eragiketa bi aldeen arteko konparazioa.
Orokorrean, bi esanahi nagusi dituen kontzeptua da. Lehenak, harmonia edo ikuspegi estetikotik, proportzionaltasun eta oreka atsegineko sentsazio lausoa du[3][4], edertasuna edo perfekzioa islatzen duena. Hori dela eta, simetria sinbolo eta kultur artefaktu ugaritan agertzen da, psikologo batzuen arabera gizakiak, instintiboki, harmonia simetrikoa bilatzen baitu; sexu-erakarpenarekin ere erlazionatu liteke, aurpegi simetrikoenak izanik erakargarritzat jo ohi direnak, komunzki.
Bigarren esanahia, sistema formal baten arauen arabera, frogatu edo froga daitekeen oreka edo autoantzekotasun eredua kontzeptu zehatza eta ondo definitua da: geometriaren bidez, fisikaren bidez edo beste diziplina batzuen bidez. Testuinguru batzuetan, esanahiak desberdinak badira ere, simetriaren bi adierak erlazionatuta daude, eta paraleloki aztertzen dira.
Simetria forma geometrikoen, sistemen, ekuazioen eta beste objektu materialen edo entitate abstraktuen ezaugarri bat da, eraldaketa, mugimendu edo truke jakin batzuen azpian duten aldaezintasunari lotuta dagoena. Termino formaletan, objektu bat eragiketa matematiko jakin baten aldean, simetrikoa dela esaten dugu, baldin eta objektuari aplikatzen zaionean eragiketa horrek objektua edo itxura aldatzen ez duen. Eragiketa-multzo jakin bati dagokionez, bi objektu elkarren simetrikoak dira beste batetik lortzen badira eragiketa batzuen bidez (eta alderantziz). 2D geometrian, interesgarri diren simetria-klase nagusiak espazio euklidear baten isometriei dagozkienak dira: translazioak, biraketak, islapenak eta irristatze islapenak[5].
Operazio matematikoan oinarritzen bagara, objektu bat simetrikoa da operazioa aplikatu ondoren objektuak eta bere itxurak aldaketarik gabe jarraitzen dutenean.
Matematikan[aldatu | aldatu iturburu kodea]
Simetria geometrikoa[aldatu | aldatu iturburu kodea]

Jende gehienarentzat, simetria mota ohikoena, simetria geometrikoa da. Objektu geometriko bat simetrikoa dela esaten da: geometrikoki eraldatu ondoren jatorrizko objektuaren propietateren bat mantentzen badu (hau da, objektuak aldaezintasun bat badu transformazioaren azpian). Adibidez, bere baitan biratzen duen zirkulu batek jatorrizko zirkuluaren forma eta tamaina bera izango du. Orduan, zirkulu bat biraketan simetrikoa dela edo errotazio simetria duela esaten da.
Objektu fisiko edo elementu geometrikoetan simetriaz aritzean, transformazio geometrikoaz hitz egiten da: birak, translazioak eta islapenak. Objektu batek hainbat simetria mota izan ditzake:
- Simetria esferikoa: Biraketaren ondorioz matematikari dagokionez objektu fisiko baten simetria multzoa SO(3) da.[6]
- Simetria zilindrikoa: Ardatz baten inguruan egindako biraketek ez dute aldaketarik sortzen. Matematikarekin harremana duen simetria talde batean sartzen den mota da SO(2).
- Simetria islakorra: Plano bakarra egoteagatik ezaugarri den simetria islatzailea edo simetria espekularra, matematikoki O(1) taldearekin edo haren irudikapen baliokidearekin . Bi dimentsiotan, simetria-ardatza du, eta, hiru dimentsiotan, planoa du. Bi dimentsioko irudi baten simetria-ardatza zuzena da; perpendikular bat eraikitzen bada perpendikular horren gainean, simetria-ardatzarekiko distantzia berean dagoen edozein puntu berdinak dira. Hori ikusteko beste modu bat da forma ardatzaren erditik tolestuta egongo balitz; orduan, bi erdiak berdinak izango lirateke. Adibidez, karratu batek lau simetria-ardatz ditu, lau modu ezberdin baitaude tolesteko bere ertzak bat etor daitezen. Zirkulu batek simetria-ardatz infinituak izango lituzke arrazoi berarengatik.
- Translazio simetria ematen da transformazioak objektu bat aldaezin uzten duenean translazio diskretu edo jarraituen talde baten azpian. Taldea diskretua da inbariantzia a-ren balio-kopuru zenbagarri baterako bakarrik betetzen bada, eta jarraitua, alderantziz, a-ren inbariantzia baten balio multzo infinitu kontaezin baterako aurkezten bada.
Aurreko bi edo gehiago konbinatzen dituzten simetria mota batzuk hauek dira:
- Translazio kontrako simetria da lerro edo plano batean islapen bat eta ardatz horretan zeharreko translazio bat konbinatzen dituena. Simetria-taldea isomorfoa da -ri.
- Erroto-islatze simetria edo errotazio-simetria desegokiak dakar ardatz baten inguruan biraketa, errotazio-ardatzarekiko perpendikularra den ardatz batean islatzearekin konbinatuta.
- Simetria helikoidalak suposatzen du ardatz jakin baten inguruan biraketa-mugimendua, ardatz berean, bere baitan, emandako translazio-mugimendu batekin. Hiru motatakoa izan daiteke:
- Simetria helikoidal infinitua.
- n ardatzen simetria helikoidala.
- Errepikatzen ez den simetria helikoidala.
Logikan[aldatu | aldatu iturburu kodea]
R = S × S erlazio bitar simetrikoa da S-ko a, b elementu bakoitzeko, Rab egia den bitartean, Rba[7] ere egia izango da. Beraz, adin berekoa da erlazioa simetrikoa da, zeren Pablok Maríaren adina badu, orduan, Maríak Pabloren adina du.
Proposizio-logikan, lokailu logiko bitar simetrikoek eta (∧, edo &), edo (∨, edo |) eta baldin eta soilik baldin (↔) barne hartzen dituzte, baldin eta (→) lokailua simetrikoa ez den bitartean[8]. Beste lokailu simetriko logikoen artean barne hartzen dituzte: ez eta (ez-eta, edo ⊼), xor (ez-bibaldintzazkoa edo ⊻) eta Ez-edo (ez-edo, edo ⊽).
Matematikaren beste arlo batzuk[aldatu | aldatu iturburu kodea]
Objektu matematiko bat eragiketa matematiko jakin baten aldean simetrikoa dela esan daiteke, baldin eta, objektuari aplikatuta, eragiketa horrek objektuaren propietateren bat gordetzen badu[9]. Objektuaren propietate jakin bat gordetzen duten eragiketen multzoak talde bat osatzen du.
Oro har, matematikako egitura mota bakoitzak bere simetria mota izango du. Adibideak kalkuluko funtzio bikoitiak eta bakoitiak hartzen duten bere baitan daude: aljebra abstraktuko talde simetrikoak, aljebra linealeko matrize simetrikoak[10] eta Galoisen teoriako Galois taldeak. Estatistikan, simetria probabilitate-banaketa simetriko gisa eta asimetria gisa ere agertzen da: banaketaren asimetria[11].
Simetria artean[aldatu | aldatu iturburu kodea]
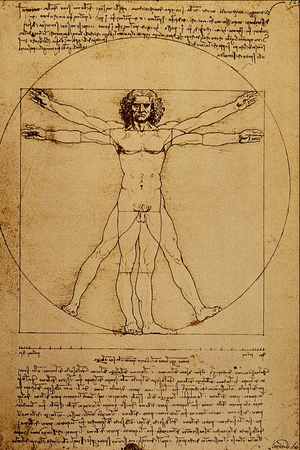
Arkitekturan[aldatu | aldatu iturburu kodea]
Simetria eskala guztietan dago arkitekturan, hasi eraikinen kanpoko bista orokorretatik (katedral gotiko eta Etxe Zuriaraino, adibidez) edo solairuen diseinutik banakako eraikuntza-elementuen diseinura (baldosa-mosaikoak, esaterako). Eraikin islamiarrek, hala nola Taj Mahal eta Lothostahko meskitak, simetriaren erabilera landua egiten dute, bai egituran, bai ornamentazioan.[12][13] Alhambra moduko eraikin moriskoak patroi konplexuz apainduta daude, translazio- eta islapen-simetriak eta errotazioak erabiliz.[14]
Arkitektura modernista, nazioarteko estiloarekin hasita, «hegaletan eta masa-orekan» oinarritzen da, ordea.[15]
Marrazketan[aldatu | aldatu iturburu kodea]
Marrazketan bost simetria mota daude: translazioa, errotazioa, handitzea, aldebiko simetria eta eraispena.
- Translazio-simetria edo inbariantzia translazionala: Lerro batean zehar, forma bat errepikatzea da, edozein posiziotan (bertikalean, horizontalean, diagonalean edo kurban) ardatzarekiko edozein distantzia konstantera mugituz.
- Errotazioa: Zenbait aldiz errepikatzen den motibo baten biraketa-simetria, hasierako bera izan arte, ordena jakin bat du errotazioan (15 º, 30 º, 45 º, 60 º, 90 º, 360 º bitarte). Forma barruan egon daitekeen zentro baten inguruan dago.
- Handitze-simetria: Haren zatiak antzekoak dira, forma bera baitute, baina ez tamaina bera, zentrotik kanporantz zabaltzen baita gero eta handiagoa izateko.
- Eraispen-simetria: Biraketa-ardatzak bi zati berdin-berdin erakusten dizkigu, bata bestearekiko 180 º-ko biraketarekin.
- Simetria aldebikoa: Aldebiko erretratua, ardatz baten bi aldeetatik distantzia berera dauden forma berdinek osatzen dute, hori guztia simetria-ardatz baten barruan.
Alfonbra eta tapetetan[aldatu | aldatu iturburu kodea]
Alfonbretan, simetria erabiltzeko tradizio luzeak hainbat kultura hartzen ditu bere baitan. Amerikako navajo indiarrek diagonal beltz ausartak eta motibo angeluzuzenak erabiltzen zituzten. Ekialdeko alfonbra askok erdigune korapilatsuak eta patroi bat jarraitzen duten ertz ispilatuak dituzte. Ez da harritzekoa alfonbra angeluzuzenek, normalean, laukizuzen baten simetriak edukitzea, hau da, ardatz horizontalean zein bertikalean islatzen diren motiboak[16][17].
Ohazaletan[aldatu | aldatu iturburu kodea]
Ohazalak bloke karratuz egiten direnez (oro har, 9, 16 edo 25 pieza bloke bakoitzeko) eta bakoitza pieza txikiagoz eta, oro har, oihal-triangeluz osatuta dagoenez, eskulanak erraztu egiten du simetria aplikatzea[18].
Beste arte eta lanbideetan[aldatu | aldatu iturburu kodea]

.
Mota guztietako objektuen diseinuan, simetriak agertzen dira. Adibideak barne hartzen dute beira-aleak, altzariak, hareazko pinturak, korapiloak, maskarak eta musika tresnak. Simetriak funtsezkoak dira M. C. Escherren artearentzat, baita arte eta artisautza formetan mosaikoaren aplikazio ugarietan ere, hala nola horma-paperetan, zeramikazko teila islamiar dekorazio geometrikoan, batik, ikat, alfonbragintzan eta ehungintza-eredu eta brodatu mota askotan[19].
Logotipoaren diseinuan ere, simetria erabiltzen da[20]. Simetriaren teoria erabiliz logotipo bat lauki-sare batean sortzean, diseinatzaileek beren lana antola dezakete; diseinu simetriko edo asimetriko bat sor dezakete; letren arteko espazioa zehaztu; diseinuan zenbat espazio negatiboa behar den zehaztu; eta nola azpimarratu logoaren zatiak nabarmentzeko.
Estetikan[aldatu | aldatu iturburu kodea]
Simetriak estetikarekin duen harremana konplexua da. Gizakiak, fisikoki aurpegi erakargarrietan, aldebiko simetria aurkitzen dute[21][22]; osasuna eta egokitasun genetikoa adierazten du[23]. Horri, gehiegizko simetria aspergarritzat edo interesik gabekotzat hartzeko joerari, aurre egiten dio. Jendeak nahiago du nolabaiteko simetria duten formak, baina interesgarriak egin ditzaketen konplexutasun nahikoarekin[24].
Literaturan[aldatu | aldatu iturburu kodea]
Simetria hainbat formatan aurki daiteke literaturan, adibide sinple bat palindromoa da, non testu labur bera aurrera edo atzera irakurri daitekeen. Istorioek egitura simetrikoa izan dezakete, Beowulf-en igoera/jaitsiera ereduan bezala[25].
Simetria fisikan[aldatu | aldatu iturburu kodea]
Fisika arloan, simetria ez du zertan forma geometrikoetan oinarritu. K objektu matematikoen multzoa da (funtzioak, forma geometrikoak, ekuazioak, etab.), G, aldiz, transformazio multzoa da, eta K-ren gainean jokatzen du, modu honetan:[26]
duen elementu batek simetria izango du honako baldintza hau betetzen bada:
Hori dela eta, fisikako iraupenaren legeak lagrangear simetria abstraktuen existentziaren ondorioak dira, Noether teoremak islatzen duen bezala. Teorema honetan, K lagrangearrak multzo onarkorrak irudikatzen ditu; K0</subV lagrangearrak sistema baxuarenak, eta G-k gauza asko irudikatu ditzake:
- Translazio espazialak: momentu linealaren iraupena
- Aldi baterako translazioak: energiaren iraupena
- Biraketak: momentu angeluarraren iraupena
- Simetria abstraktuak: karga elektrikoaren iraupena, leptoia, parekidetasuna, eta abar.
- 1. Adibidea. Lehen adibide gisa har dezagun uniformeki kargatutako bi plaka infinitu artean higitzen den elektroi bat (sistema hori kondentsadore mota jakin bati hurbiltzen da, gutxi gorabehera): planoekiko paralelo den edozein translazio sistema fisikoaren simetria osatzen duenez, aipatutako planoekiko indar paraleloa nulua da, eta, beraz, paraleloen abiadura konstantea da planoekiko.
- 2. Adibidea. Har dezagun simetria esferiko perfektua duen gorputz baten (planeta edo izar) inguruan orbitatzen duen satelite bat; gogoan har dezagun, gainera, satelitearen abiadura satelitearen erdigunearen eta gorputzaren arteko lerroarekiko perpendikularra dena. Kasu horretan, ardatz baten inguruko errotazioei dagokienez, lagrangiarra guztiz aldaezina da eremu grabitatorioaren iturburuaren erdigunetik pasatzean. Kasu horretan, bai Lagrangiarren zein hasierako higidura-baldintzen errotazio-simetria dela eta, planetarekiko perpendikularra den abiadura konstantea da, eta ibilbidea orbitaren planoarekiko perpendikularra den errotazioaren pean zirkulu aldaezina da.
Aurreko bi adibide horiek Noether-en teoremaren kasuak dira, emaitza orokorrak adierazten duena parametro bakarreko G simetria-talde bat existitzen bada Lagrangiarrentzat, hala nola:
Orduan kantitate eskalarra:
v izanik parametro bakarreko simetria-eraldaketa-taldea sortzen duen eremu bektoriala, eta pi posizio-koordenatu orokortuen momentu konjugatuak.
Simetria kimikan[aldatu | aldatu iturburu kodea]
Kimika arloan, simetria geometrikoak garrantzi handia du molekuletan, molekulak sailkatzeko balio baitu. Horretaz gain, memento dipolarraren propietateak eta trantsizio espektroskopiko onartuak (hautatzeko arauetan oinarrituta) molekularen simetriaren bidez aurresan edo azaldu daitezke.[27] Kimikan agertzen diren simetriak lotuta daude isometriako mugagabeen multzora, zehazkiago, isometriaren transformazioen talde puntualetara.
Simetria biologian[aldatu | aldatu iturburu kodea]

Biologian, simetria bikoiztuta agertzen diren gorputzeko organismoen banaketa orekatua da. Organismo zelulanitzen gehienek forma simetrikoa dute, hau da, simetria erradial zein aldebiko simetria. Hala ere, gutxiengo batek ez du inolako simetriarik azaltzen (hau da, asimetrikoak dira).[28]
Simetria erradiala[aldatu | aldatu iturburu kodea]
Simetria mota hori ardatz heteropolar balitz gisa definitzen da (ezberdina bi ertzetan). Ahoa duen ertzari, ahozko alboa deritzo, eta, kontrako ertzari, abaktinal edo aborala. Ardatz horretan, simetriako plano nagusiak finkatzen dira: Per-erradikalak definitzen dituzten bi perpendikularrak. Beste planoetako egiturak (per-erradikalen erdikariak) inter-erradikalean geratzen dira. Per-erradikal eta inter-erradikal eremuen artean, ad-erradikala kokatzen da
Aldebiko simetria[aldatu | aldatu iturburu kodea]

Itsas izarrak eta trikuak bezalako animaliek bigarren mailako simetria erradiala agertzen dute (garapenaren aldi goiztiarrekoak eta larbek duten aldebiko simetria helduak direnean desagertzen da). Hala ere, animalia gehienek aldebiko simetria dute, eta, beraz, aldebikotasun taldearen barruan sartu genitzake. Aldebiko simetriak mugimenduaren norabidearekiko ardatzaren definizio bat zilegitzen du, eta horrek sistema nerbioso zentralizatu baten formazioan laguntzen du.
Psikologia eta neurozientzian[aldatu | aldatu iturburu kodea]
Giza behatzailearentzat, simetria mota batzuk beste batzuk baino nabarmenagoak dira; bereziki nabarmenena ardatz bertikala duen isla da, giza aurpegian dagoena, adibidez. Ernst Machek Sentsazioen analisia liburuan egin zuen behaketa hori[29], eta horrek esan nahi du simetriaren pertzepzioa ez dela era guztietako erregulartasunen erantzun orokorra. Jokabide zein neurofisiologia-ikerketek, simetria islatzailearenganako sentsibilitate berezia dela baieztatu dute gizakietan eta beste animalietan ere[30]. Gestalt tradizioko lehen ikerketek iradoki zuten aldebiko simetria pertzepzio-multzoaren funtsezko faktoreetako bat zela. Hori simetriaren printzipioa bezala ezagutzen da. Simetriaren papera, irudi/zoruaren taldekatze eta antolaketan, azterketa askotan baieztatu da. Esaterako, islapen-simetriaren detekzioa azkarragoa da hori objektu bakar baten propietatea denean[31]. Psikofisikoen eta gizakien pertzepzio-ikerketek simetriaren detekzioa azkarra, eraginkorra eta sendoa dela nahasteetarako erakutsi dute. Adibidez, simetria detekta daiteke 100 eta 150 milisegundo arteko aurkezpenekin[32].
Neuroirudi-ikerketa berriagoek dokumentatu dute garuneko zein eskualde dauden aktibo simetriaren pertzepzioan. Sasakik eta beste batzuek[33] erresonantzia magnetiko funtzionalaren irudia (fMRI) erabili zuten ereduen erantzunak puntu simetriko edo ausazkoekin alderatzeko. Aktibitate handia zegoen kortex okzipitalaren eskualde estraildaskatuetan, baina ez ikusizko kortex primarioan. Estraildaskatuako eskualdeek barne hartu zuten V3A, V4, V7 eta alboko okzipital konplexua (LOC). Ikerketa elektrofisiologikoek, eremu bereko jatorrian, atzealdeko negatibotasun berantiarra aurkitu dute[34]. Orokorrean, ikusmen-sistemaren zati handi batek simetria bisualaren prozesamenduan parte hartzen duela dirudi, eta eremu horiek ikusizko simetria detektatzeko eta objektuak ezagutzeko ardura dutenen antzeko sareak dute tartean[35].
Musikan[aldatu | aldatu iturburu kodea]
Musika klasikoan, badaude konposizioak, non aldebiko simetria, translazioa edo bira erdiak sortutako noten banaketak aurki ditzakegun. Konposizioen adibide batzuk hauek dira: Johann Sebastian Bachen, Preludioa; Domenico Scarlattiren, Sonata Sol maiorrean; Robert Schumannen, Lotosblume; edo, Richard Wagnerren, Die Meistersinger.
Tonuaren egiturak[aldatu | aldatu iturburu kodea]
Simetria ere garrantzitsua da eskala eta akordeen eraketaren kontuan, musika tradizionala edo tonala tonu talde ez-simetrikoek osatzen baitute, hala nola eskala diatonikoa edo akorde nagusia. Eskala edo akorde simetrikoek (tonu-eskala osoa, akorde handitua edo zazpigarren akorde txikitua) norabiderik edo aurrera egiteko zentzurik ez dutela esan izan da; anbiguoak dira tonalidade edo tonu-zentroarekiko, eta funtzionalitate diatoniko ez hain zehatza dute. Hala ere, Alban Berg, Béla Bartók eta George Perle gisako konpositoreek simetria-ardatzak edo/eta tarte-zikloak tonalidade edo tonu-zentro ez-tonalen antzera erabili izan dituzte[36].
Tarte-zikloak simetrikoak dira, eta, beraz, ez dira diatonikoak. Hala ere, Do-5eko zazpi tonuko segmentu batek (Bostunen zirkulua, laugarrenen zikloarekin enarmonikoak direnak) eskala diatoniko nagusia sortuko du. Gustav Mahler eta Richard Wagner gisako konpositore erromantikoen lanetako progresio tonal ziklikoek, horrenbestez, lotura bat osatzen dute modernisten musika atonalaren progresio ziklikoekin, hala nola Bartók, Alexander Scriabin, Edgard Varèse eta Vienako eskola. Aldi berean, progresio horiek tonalitatearen amaiera adierazten dute[36][37].
Harreman tonal simetrikoetan oinarritutako lehen konposizio hedatua ziurrenik Alban Berg Quartet, op. 3 (1910) izan zen[37].
Korronte aldizkatzailearekin[aldatu | aldatu iturburu kodea]
Irrati-maiztasun elektronikoaren testuinguruan, korronte aldizkatzaile edo alternoko hornidura simetrikoaz hitz egiten da eroale bat lurrera ez doanean. Eroaleetako bat lurrera doanean eta besteak tentsio-aldaerak jasaten dituenean, elikadura-iturria asimetrikoa dela esaten da.
Badaude elikadura simetrikoan oinarritutako aplikazio teknologiko garrantzitsuak, elikadura simetrikoak abantaila handia baitu transmisio-lerroan potentzia-galera magnitude ordena txikiagoa delako kable ardazkidearen bidezko elikadura asimetrikoa baino.
- Izan ere, gorako eroaleak sortzen duen eremu alternoa bere beheranzkoak sortutako eremuak ezeztatzen du.
- Horrez gain, delta elikadura simetrikoak eraikuntza errazteko aukera ematen du.
Jario orekatua da, beraz, QRP funtzionamenduan eta EME moduan, non irabazitako dB bakoitzak balio duen.
Ikus, gainera[aldatu | aldatu iturburu kodea]
Estatistikan[aldatu | aldatu iturburu kodea]
Literaturan[aldatu | aldatu iturburu kodea]
Simetria moralari buruz[aldatu | aldatu iturburu kodea]
Enpatia eta sinpatia Urrezko araua
Fisikan[aldatu | aldatu iturburu kodea]
Beste batzuek[aldatu | aldatu iturburu kodea]
Erreferentziak[aldatu | aldatu iturburu kodea]
- ↑ (Gaztelaniaz) Alej; MaculetCurs, ro; Finanzas, o actualmente el Grado de Maestro en Educación Primaria en la Universidad Autónoma de Madrid Técnico Superior en Administración y; Quiromasajista; naturaleza, Masajista Deportivo y Músico Forma parte del equipo de desarrollo de contenidos de Smartick Curioso por; Pasiones, Música Y. Ciencia Son Dos De Sus. (2018-09-17). «Simetría: qué es en matemáticas y ejercicios» Smartick (Noiz kontsultatua: 2022-11-12).
- ↑ Diccionario de Arte II (gaztelaniaz). Barcelona: Biblioteca de Consulta Larousse. Spes Editorial SL (RBA), 2003, 241. or. DL M-50.522-2002. ISBN 84-8332-391-5 [2014-12-08an begiratua].
- ↑ Penrose, Roger. Fearful Symmetry. City: Princeton, 2007. ISBN 9780691134826
- ↑ (Katalanez) Aristòtil. 2023-04-24 (Noiz kontsultatua: 2023-05-20).
- ↑ Guillermo, Roa Zubia. (2004-11-01). «Simetria ez da beti lege» Zientzia.eus (Noiz kontsultatua: 2022-11-12).
- ↑ Wald, Robert M.. (1984). General relativity. Chicago University Press ISBN 0-226-87032-4...
- ↑ Josiah Royce, Ignas K. Skrupskelis (2005) The Basic Writings of Josiah Royce: Logic, loyalty, and community (Google eBook) Fordham Univ Press, 790. or.
- ↑ Gao, Alice (2019). «Propositional Logic: Introduction and Syntax». University of Waterloo — School of Computer Science. 2019-11-12an begiratua.
- ↑ Christopher G. Morris (1992) Academic Press Dictionary of Science and Technology Gulf Professional Publishing
- ↑ (Ingelesez) https://facebook.com/mathvault. (2019-08-01). The Definitive Glossary of Higher Math Jargon | Math Vault. (Noiz kontsultatua: 2023-05-22).
- ↑ (Ingelesez) Petitjean, Michel. (2003-09). «Chirality and Symmetry Measures: A Transdisciplinary Review» Entropy 5 (3): 271–312. doi:. ISSN 1099-4300. (Noiz kontsultatua: 2023-05-22).
- ↑ Williams: Symmetry in Architecture. Members.tripod.com (1998-12-31). Retrieved on 2013-04-16.
- ↑ Aslaksen: Mathematics in Art and Architecture. Math.nus.edu.sg. Retrieved on 2013-04-16.
- ↑ ISBN 978-1-4008-2311-6..
- ↑ Dunlap, David W.. (2009-07-31). «Behind the Scenes: Edgar Martins Speaks» New York Times.
- ↑ «Marla Mallett Textiles, Antique Tribal Oriental Rugs, Kilims and Tapestries» web.archive.org 2001-02-03 (Noiz kontsultatua: 2023-05-22).
- ↑ «navajocentral.org» navajocentral.org (Noiz kontsultatua: 2023-05-22).
- ↑ Quate: Exploring Geometry Through Quilts 2003-12-31an begiratua Wayback Machinen.. Its.guilford.k12.nc.us. Retrieved on 2013-04-16.
- ↑ Cucker, Felipe (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. pp. 77–78, 83, 89, 103. ISBN 978-0-521-72876-8
- ↑ (Ingelesez) «How to Design a Perfect Logo for Your Company» Design Mantic (Noiz kontsultatua: 2023-05-22).
- ↑ (Ingelesez) Grammer, Karl; Thornhill, Randy. (1994). «Human (Homo sapiens) facial attractiveness and sexual selection: The role of symmetry and averageness.» Journal of Comparative Psychology 108 (3): 233–242. doi:. ISSN 1939-2087. (Noiz kontsultatua: 2023-05-22).
- ↑ Jones, B. C., Little, A. C., Tiddeman, B. P., Burt, D. M., & Perrett, D. I. (2001). Facial symmetry and judgements of apparent health Support for a “‘ good genes ’” explanation of the attractiveness – symmetry relationship, 22, 417–429.
- ↑ Rhodes, Gillian; Zebrowitz, Leslie, A. (2002). Facial Attractiveness - Evolutionary, Cognitive, and Social Perspectives. Ablex. ISBN 1-56750-636-4
- ↑ Arnheim, Rudolf. (1969). Visual thinking. Berkeley, University of California Press (Noiz kontsultatua: 2023-05-22).
- ↑ Jenny Lea Bowman (2009). «Symmetrical Aesthetics of Beowulf». University of Tennessee, Knoxville.
- ↑ (Gaztelaniaz) Simetrías en física. Parte I: Qué son, cómo se describen y qué tipos hay – Física Tabú. (Noiz kontsultatua: 2022-11-12).
- ↑ «Química Inorgánica Estructural - Elementos de simetría y Operaciones de simetría» dqino.ua.es (Noiz kontsultatua: 2022-11-12).
- ↑ «4.3. Simetría» www.biologia.edu.ar (Noiz kontsultatua: 2022-11-12).
- ↑ Mach, Ernst (1897). Symmetries and Group Theory in Particle Physics: An Introduction to Space-Time and Internal Symmetries. Open Court Publishing House.
- ↑ Wagemans, Johan. (1997-12). «Characteristics and models of human symmetry detection» Trends in Cognitive Sciences 1 (9): 346–352. doi:. ISSN 1364-6613. (Noiz kontsultatua: 2023-05-23).
- ↑ (Ingelesez) Bertamini, Marco. (2010-01). «Sensitivity to Reflection and Translation is Modulated by Objectness» Perception 39 (1): 27–40. doi:. ISSN 0301-0066. (Noiz kontsultatua: 2023-05-23).
- ↑ (Ingelesez) Barlow, H. B.; Reeves, B. C.. (1979-01-01). «The versatility and absolute efficiency of detecting mirror symmetry in random dot displays» Vision Research 19 (7): 783–793. doi:. ISSN 0042-6989. (Noiz kontsultatua: 2023-05-23).
- ↑ (Ingelesez) Sasaki, Yuka; Vanduffel, Wim; Knutsen, Tamara; Tyler, Christopher; Tootell, Roger. (2005-02-22). «Symmetry activates extrastriate visual cortex in human and nonhuman primates» Proceedings of the National Academy of Sciences 102 (8): 3159–3163. doi:. ISSN 0027-8424. PMID 15710884. PMC PMC549500. (Noiz kontsultatua: 2023-05-23).
- ↑ (Ingelesez) Makin, Alexis D. J.; Rampone, Giulia; Pecchinenda, Anna; Bertamini, Marco. (2013-09). «Electrophysiological responses to visuospatial regularity: Electrophysiological responses to visuospatial regularity» Psychophysiology: n/a–n/a. doi:. (Noiz kontsultatua: 2023-05-23).
- ↑ (Ingelesez) Bertamini, Marco; Silvanto, Juha; Norcia, Anthony M.; Makin, Alexis D.J.; Wagemans, Johan. (2018-08). «The neural basis of visual symmetry and its role in mid- and high-level visual processing: Neural basis of visual symmetry» Annals of the New York Academy of Sciences 1426 (1): 111–126. doi:. (Noiz kontsultatua: 2023-05-23).
- ↑ a b (Ingelesez) Perle, George. (1992-01). «Symmetry, the twelve-tone scale, and tonality» Contemporary Music Review 6 (2): 81–96. doi:. ISSN 0749-4467. (Noiz kontsultatua: 2023-05-23).
- ↑ a b Perle, George (1990). The Listening Composer. University of California Press. p. 21. ISBN 978-0-520-06991-6








