Zirrikitu bikoitzaren saiakuntza

| Artikulu sail baten zatia |
| Mekanika kuantikoa |
|---|
Fisika modernoan, zirrikitu bikoitzaren saiakuntza, argiak eta materiak klasikoki definitutako uhin eta partikulen ezaugarriak adierazi ditzaketela erakusten du; gainera, fenomeno mekaniko kuantikoen funtsezko izaera probabilistikoa erakusten du. Esperimentu mota hau Thomas Young-ek egin zuen lehen aldiz, argia erabiliz, 1801ean, argiaren uhin portaeraren erakusgarri gisa. Garai hartan argia uhinez edo partikulaz osatuta zegoela uste zen. Fisika modernoaren hasierarekin, ehun urte geroago, argi geratu zen argiak, uhinen zein partikulen ezaugarriak zituen portaera erakutsi zezakeela. 1927an, Davissonek eta Germerrek frogatu zuten elektroiek konportamolde bera zutela, non, beranduago, atomo eta molekuletara hedatu zen portaera berbera. [1] [2] Thomas Young-ek argiarekin egindako esperimentua fisika klasikoaren parte zen eta mekanika kuantikoa eta uhin-partikula dualtasunaren kontzeptua baino askoz lehenagokoa. Argiaren uhin teoria zuzena zela frogatu zuela uste zuen eta bere esperimentua Young-en esperimentua [3] edo Young-en zirrikituak bezala aipatzen da ere.
Eskala atomikoko beste entitate batzuetan, elektroiak esate baterako, portaera bera erakusten dute zirrikitu bikoitz batera jaurtitakoan. [4] Gainera, banakako inpaktu diskretuen detekzioa berez probabilistikoa dela antzematen da. Mekanika klasikoa erabiliz ez da posible gertaera hori azaltzea. [4]
Elektroiak eta protoiak baino handiagoak diren entitateekin egin daiteke esperimentua, baina zenbat eta tamaina handiagotu orduan eta zailagoa egiten da esperimentua burutzea.. Zirrikitu bikoitzeko esperimentuarekin egin diren entitate handienak 810 atomo biltzen zituzten molekulak izan ziren (non masa osoa 10.000 masa atomikotik gorakoa zen). [1] [2]
Zirrikitu bikoitzeko esperimentua (eta bere aldakuntzak) pentsamendu esperimentu klasiko bihurtu da, mekanika kuantikoaren enigmak adierazteko duen zehaztasunagatik. Behatzaileak emaitza esperimentalak aurreikusteko duen gaitasunaren funtsezko muga erakusten duenez, Richard Feynman-ek "fenomeno hori [...] modu klasikoan azaltzea ezinezkoa da eta mekanika kuantikoaren bihotza du bere baitan. Errealitatean , [mekanika kuantikoaren] misterio bakarra dauka. [4]
Sarrera
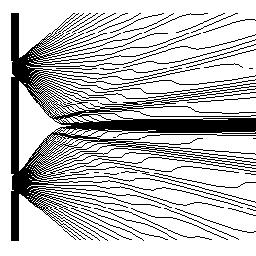
[aldatu | aldatu iturburu kodea]Argia partikula arrunt edo klasikoz osatuta egongo balitz, eta partikula horiek lerro zuzenean jaurti egingo balira zirrikitu baten bidez eta beste aldean dagoen pantaila bat jotzen utziko balitz, zirrikituaren tamainari eta formari dagokion eredua ikusiko genuke. Hala ere, "zirrikitu bakarreko esperimentu" hau benetan egiten denean, pantailako eredua argia hedatzen den difrakzio eredua da. Zirrikitua zenbat txikiagoa izan, orduan eta hedapen angelua handiagoa da. Irudiaren goiko zatiak laser gorri batek zirrikitu bat argiztatzen duenean eratutako ereduaren erdiko zatia erakusten du eta, arretaz begiratzen bada, bi banda ahul. Banda gehiago ikus daitezke aparatu zehatzago batekin. Difrakzioak, eredu honek zirrikituaren argi uhinen interferentziaren emaitza dela azaltzen du.

Partikula uhinaren funtzioaren simulazioa: zirrikitu bikoitzeko esperimentua. Desfokuratze zuriak uhina irudikatzen du. Zenbat eta pixel zuriagoa izan, orduan eta probabilitate handiagoa egongo da partikula bat aurkitzeko leku konkretu horretan neurtu nahi bada. Bi zirrikitu paralelo argiztatzen badira, bi zirrikituetako argiak berriro interferituko du. Hemen interferentziak eredu nabarmenagoak dira, banda argi eta ilunak txandakatuz. Banden zabalera argiztatzen den argiaren maiztasunaren propietatea da. [5] (Ikus eskuinaldeko beheko argazkia.) Thomas Young-ek (1773-1829) fenomeno hau lehenengo aldiz frogatu zuenean, argia uhinez osatuta zegoela adierazi zuen, distiraren banaketa uhin-fronteen interferentzia alternatibo gehigarri eta kenketaz azal daitekeelako. [4] Young-en esperimentuak, 1800. hamarkadaren hasieran, berebiziko garrantzia izan zuen argiaren uhin teoria ulertzeko, Isaac Newton-ek proposatutako argiaren teoria korpuskularra garaituz, non XVII. eta XVIII. mendeetan argiaren hedapen eredu onartua hau izan zen. Hala ere, efektu fotoelektrikoaren aurkikuntza geroago frogatu zen egoera desberdinetan argiak partikula diskretuz osatuta egongo balitz bezala joka dezakeela. Itxuraz kontrajarriak ziren aurkikuntza horiek fisika klasikoaren garapena eta argiaren izaera kuantikoa kontuan hartzera ereman zuten.
Feynmanek gogoko zuen esatea esperimentu bakar honen ondorioak arretaz pentsatzetik atera daitekeela mekanika kuantiko guztia. [6] Gainera, proposatu zuen (pentsamendu esperimentu gisa) detektagailuak zirrikitu bakoitzaren aurretik jarriz gero, interferentzia eredua desagertuko zela. [7]
Englert - Greenberger dualtasun erlazioak zirrikitu bikoitzeko interferentziaren matematika tratamendu zehatza eskaintzen du mekanika kuantikoaren testuinguruan.
Intentsitate baxuko zirrikitu bikoitzeko esperimentua G. I. Taylor-ek egin zuen lehen aldiz 1909an, [8] argi gorabeheratsuaren maila murriztuz fotoi igorpen / xurgapen gertaerak gainjarri ez ziren arte. Zirrikitu bikoitzeko esperimentua ez zen argia ez zen beste ezerrekin egin 1961 arte, Claus Jönsson Tubingeko Unibertsitateko elektroien izpiekin egin zuen arte. [9] [10] 1974an, Pier Giorgio Merli, Gian Franco Missiroli eta Giulio Pozzi fisikari italiarrek elektroi bakarrak eta bi prisma erabiliz (zirrikituen ordez) errepikatu zuten esperimentua, elektroi bakoitzak teoria kuantikoak aurreikusten duen bezala bere buruarekin interferitzen dela erakutsiz. [11] [12] 2002an, esperimentuaren elektroi bakarreko bertsioa "esperimentu ederrena" izendatu zuten Physics World-eko irakurleek. [13]
2012an, Stefano Frabbonik eta bere lankideek azkenean zirrikitu bikoitzeko esperimentua egin zuten elektroiekin eta benetako zirrikituekin, Feynmanek proposatutako jatorrizko eskemari jarraituz. Elektroi bakarrak nanofabrikatutako zirrikituetara bidali zituzten (100 nm inguruko zabalera zutenak) eta, transmititutako elektroiak elektroi bakarreko detektagailu batekin bilduz, zirrikitu bikoitzeko interferentzia eredu baten eraketa erakutsi zezaketen. [14]
2019an, partikula bakarreko interferentzia frogatu zuten antimateriarako Marco Giammarchi-k eta lankideek [15].
Esperimentuaren aldakuntzak
[aldatu | aldatu iturburu kodea]Partikula indibidualen interferentzia
[aldatu | aldatu iturburu kodea]
Esperimentu honen aldakuntza garrantzitsu honek partikula indibidualak erabiltzen ditu. Partikulak indibidualki zirrikitu bikoitza duen aparatuan zehar bidaltzen dira eta hauek pantailan ageri dira, espero bezala. Halaere, partikula hauek banan-banan igarotzean interferentzia patroi bat antzematen da (irudian ikusi dezakegun bezala). Honek uhin-partikula dualtasuna frogatzen du,hau da, materia den guztiak uhin edo partikula propietateak erakusten dituela: partikula kokapen eta pultsazio bakarrean neurtzen da, bestetik uhinak pantailaren puntu zehatz bateko xurgapen probabilitatea deskribatzen du.[16] Fenomeno hau fotoi, elektroi, atomo eta molekula batzurekin, bucky bolak barne,gertatzen dela frogatu da.[17][18][19][20][21]
Detekzio probabilitatea uhinaren anplitudearen erro karratua da eta uhin klasikoekin kalkulatu daiteke (beheran ikusi daitekeen bezala). Fisika kuantikoaren sorkuntza geroztik, zenbait aditu determinante gehigarriak edo "aldakuntza ezkutuak" bilatzen saiatu dira , hauek aurkituz gero talka indibidual bakoitzaren jomuga kokapen zehatza lortu ahal izango zen.[22]
Mach-Zehnder interferometroa
[aldatu | aldatu iturburu kodea]
Mach –Zehnder-en interferometroa, zirrikitu bikoitzaren experimentuaren eredu sinplifikatutzat har dezakegu. Kasu honetan, fotoiak bi bidetan zehar hedatu daitezke eta bi fotodetektagailu diskreturen aurka talka egin. Bi zirrikitukoan aldiz, fotoiak espazio askean zehar hedatzen dira, bi zirrikituen ondoren, eta pantailaren edozein punturen aurka talka egiten dute. Interferometroaren bidez, algebra lineal sinplea erabiliz bi dimentsioko garapena erabili dezakegu, ekuazio diferentzialak erabili behar izatea ekidinez.
Laserraren bidez igorritako fotoiak lehen habe banatzaileari eragiten dio eta bi bide posibleen arteko gainezarmena geratzen da. Bigarren habean,bide hauen arteko interferentzia gertatzen da; fotoiak eskuineko fotodetektagailuaren aurka talka eginez bateko probabilitatearekin eta behekoan berriz, zeroko probabilitatearekin. Interesgarria izango litzateke fotoiak bi habeen arteko bi bideetan egongo balitz zer gertatuko litzatekeen aztertzea.Posible izango litzateke fenomeno hau aztertzea , bide hauetako bat oztopatuz edo fotoia bertan dagoela hautemanez. Bi kasuetan, ez litzateke bideen artean interferentziarik egongo eta bi fotodetektagailuen aurkako talka ½-ko probabilitatekoa izango litzateke. Honen bidez, ondoriozta dezakegu fotoiak ez duela bide bat edo bestea hartzen lehenengo habearen banatzearen ondoren,baizik eta gainezarmena kuantikoa gertatzen dela bi bideen artean.[17]
Norabide esperimentuak eta osagarritasun printzipioa
[aldatu | aldatu iturburu kodea]Ondo pentsatutako esperimentu mental batek iragartzen du ondokoa: partikula-detektagailuak ebakiguneetan kokatzen badira fotoiak nondik igarotzen diren bereizteko, interferentzia patroia desagertu egingo da[4]. Norabide esperimentu honek fotoiek partikula eta uhin moduan jokatzen dutela baino biak batera behatu ezin ditugula dioen osagarritasun-printzipioa erakusten digu. [23][24]
Mekanika kuantikoaren historian esperimentu mental honek garrantzia izan arren,(adb: Einstein-en esperimentu honen bertsioa) teknikoki frogagarriak ziren esperimentuak ez ziren proposatu 1970. urtera arte[25].(gendanken testuliburuan aipatutako ideia gehigarriak ez dira posibleak fotoiak ezin direlako detektatu hau xurgatu gabe) Gaur egun, osagarritasun-printzipioa frogatzen duten hainbat esperimentu egin dira.[26]
1987.urtean [27][28]egindako esperimentu batean, partikulak hartutako bidea jakin zitekeela interferentzia desagerrarazi gabe frogatu zen. Honek erakutsi zuen zein neurketa proportziok eragiten zuen gutxien mugimenduan zeuden partikulei eta ondorioz honek neurri batean inteferentziaren patroian zuen efektua. Beste modu batean esanda, fotoia zein zirrikitutik igarotzen den desberdintzeko metodoa sinesgaitzat hartzen badugu ere, neurri batean detektagarria da interferentzia patroia.[29]
Erabaki atzeratua eta ezabagailu kuantikoaren aldakuntzak
[aldatu | aldatu iturburu kodea]Wheller-en erabaki atzeratuko esperimentuek frogatu zuten, partikulak igarotako bidearen informazioa ezabatzeak, behin partikula igarota zegoela, atzera eginez partikularen aurreko jokaera aldatu lezakeela zirrikituetan.
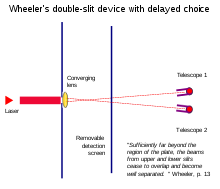
Ezabagailu kuantikoaren esperimentuek frogatzen zuten uhinen jokaera berreskuratu zitekeela hartutako bidearen informazioa ezabatzen edo eskuragarri egiten ez bagenuen.
Scientific American[30] aldizkariko artikulu batean ezabagailu kuantikoaren fenomenoa irudikatzen zuen ilustrazio sinple bat argitaratu zen. Zirrikitu bakoitzaren aurretik polarizatzaileak kokatzen badira bakoitzaren ardatza elkarrekiko ortonormal izanik, interferentzia patroia ezabatzen da. Polarizatzaileek igarotako bidearen informazioa eman diezaiokete zutabe bakoitzari. Hirugarren polarizatzaile bat kokatzen da detektagailuaren aurrean beste polarizatzaileen(ezabagailuen) ardatzarekiko 45º-ko angelua osatuz; honela interferentzia patroia berriz agerraraziz. Hau ere azal daiteke argia uhin klasikotzat[30] hartuz, eta baita ere polarizatzaile zirkularrak eta fotoi indibidualak erabiliz[31]. Kuantikoki lotutako fotoi bikoteak dituen polarizatzaileak erabiltzeak ez du azalpen klasikorik.[31]
Neurketa ahulak
[aldatu | aldatu iturburu kodea]2012an ezagutzera eman zen esperimentu honetan, ikertzaileek partikula bakoitzak hartutako bidea identifikatzea lortu zutela baieztatu zuten; inungo ondorio kontrajarririk gabe partikulek sortutako patroiaren interferentzian. Emaitza hauek lortzeko erabilitako muntaketan pantailaren aurka talka egiten zuten partikulak ez zetozten iturri puntual batetik, baizik eta bi intentsitate maximoko iturri batetik[32]. Halaere, Svensson-en[33] bezalako adituek adierazi dute ez dagoela inkongruentziarik bi zirrikituko neurketa ahul hauen eta Heisenberg-en ziurgabetasun printzipioarekin.Neurketa ahulek eta ondoren egindako aukeraketak ez zuten aldibereko posizio eta momentuaren balioak ematen partikula bakoitzerako; baina posizio desberdinetara heldutako partikulen batezbesteko ibilbidearen neurketa ahalbidetu zuten. Hau da, esperimentuak ibilbide osoaren panoramaren mapa estatistikoa sortu zuen.[33]
Beste aldakuntzak
[aldatu | aldatu iturburu kodea]1967an, Pfleegor eta Mandelek bi laser desberdin erabiliz argi iturri bezala[34], bi iturriren arteko interferentzia frogatu zuen.
1972an experimentalki frogatu zen bi zirrikituko sisteman, non zirrikitu bat irekita zegoen une oro, interferentzia behatzen zela; bide desberdintasun handia emanik fotoia zirrikitu bietako edozeinetik etorri zitekeelako. [35]Esperimentuaren baldintzen arabera fotoiaren dentsitatea sistemaren unitatea baino askoz txikiagoa zen.

1999an, bucky-bola molekulak erabiliz (bakoitzak 60 Karbono atomo ditu)[18][36] bi zirrikituko esperimentua arrakastatsu egin zen. Bucky bola mikroskopio elektronikoak ikusteko behar bezain handia da.
2005ean, E. R. Eliel-ek zulodun metal fineko pantailaren transmisio optikoaren ikerketa esperimental eta teoriko bat aurkeztu zuen. Aipatutako pantaila hainbat uhin luzeera optikoko bi azpiuhin luzerako zirrikituz banandua zegoen. Urruneko inguruneko bi zirrikituko patroiaren intentsitate totala gutxiagotu edo argi iturriaren uhin luzeraren funtzioan indartuta egongo da.[37]
2012an, Nebraska-Lincoln Unibertsitateko ikertzaileek Richard Feynman-ek deskribatu moduko bi zirrikituko esperimentua egin zuten elektroiak erabiliz. Bertan, bi zirrikituen transmisioa kontrolatzen eta elektroi askearen detekzioa monitorizatzen zuen tresna berri bat erabili zuten. Elektroiak, elektroi pistola batez jaurtiz eta bietariko 62 nm zabalera × 4 μm altuerako zirrikitu batetik igaroz.[38]
2013an, molekulak erabiliz eginiko bi zirrikituko esperimentua arrakastatsu atera zen. Molekula bakoitzak 810 atomoz (masa totala 10.000 masa atomiko unitate ) osatua zegoen. 2019an molekula barruko atomo kopuruaren errekorra 2000-ra igo zen .[39]
Uhin pilotu hidraulikoak
[aldatu | aldatu iturburu kodea]Sistema mekaniko kuantikoen hainbat alderdi simulatu ditzazketen garatutako fenomeno esperimentalak dira hidrodinamiko analogikoak, bi zirrikituko partikula askeen interferentzia barne. [40]Silikonazko olio tanta bat likidozko gainazal baten gainetik boteka doala, bere burua bultzatzen du honen uhin eremuaren erresonantziaren interakzioaz. Tantak pixkanaka zipriztintzen du likidoa bote bakoitzean. Tantak sortutako uhinek, hauekin dituen interakzioak aurretik arrarotzat hartzen ziren jokaerak erakusten dizkigu oinarrizko partikuletan. Tanta hauek sortutako uhinei pilotu uhinak deritze. Erakusten dituzten joera arraro hauek adierazten dute partikulak espazioan zehar uhin moduan zabaltzen direla kokapen espezifikorik gabe, posizioa neurtu arte.[41][42]
Sistema honen bidez simulatutako jokaerak ugariak dira: partikula kuantiko askearen difrakzioa[43], tunel efektua, orbita kuantizatuak, orbita maila bananduak, spina eta estatistika multimodala. Posible da baita ziurgabetasunaren erlazioa eta esklusio printzipioa ondorioztatzea ere. Sistemaren hainbat ezaugarri erakusten dituzten hainbat bideo daude baliagarri (Kanpo estekak).
Partikula bi edo gehiago gainezartzen dituzten sistema konplikatuagaoak ez dira azalpen sinple eta intuitubo [44]hau egiteko hain erabilgarriak. Ondorioz, ez da elkartzearen analogo hidrodinamikorik garatu[40] . Hala ere, analogia optikoak posible dira.[45]
Uhin-optikaren formulazio klasikoa
[aldatu | aldatu iturburu kodea]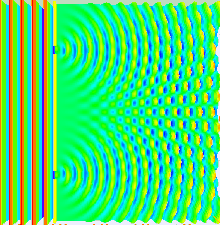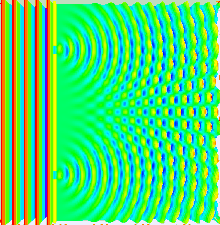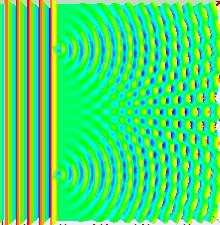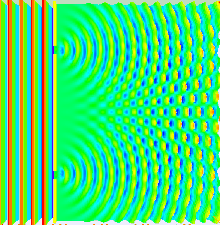
Argiaren jokaera gehiena uhinen teoria klasikoa erabiliz azaldu daiteke. Erabilitako teorietako bat Fresnel-Huygensen printzipioa da, honek dioenez uhinaren aurrealdeko puntu bakoitzak bigarren mailako uhin talde bat du. Gainera, perturbazioa edozein puntutan aurkitu daiteke uhin talde bakoitzaren ekarpena gainezarriz aukeratutako puntuan. Gehiketa honek uhin talde bakoitzaren fasea eta anplitudea hartu behar ditu kontuan. Argi iturriaren intentsitatea neurtu daiteke soilik, modulua eginez.
Bi zirrikituko esperimentuan zirrikituak laser bakarraren bitartez argiztatzen dira. Zirrikituen zabalera behar bezain txikia bada, (laserraren uhin luzeera bainu txikiagoa) zirrikituek argia difraktatzen dute uhin zilindrikoak sortuz. Bi uhin fronte zilindriko hauek gainezartu egiten dira eta anplitudea (beraz intentsitatea) uneoro magnitudearen eta fasearen menpekoak dira. Bi uhinen arteko fase bakoitza desplazatutako distantziaren desberdintasunaren menpekoa da.
Distantzia ikuskorra zirrikituen arteko distantzia baino handiagoa bada (urruneko eremua), fase desberdintasuna beheko irudian erakutsitako geometriaren bidez aurkitu daiteke. θ angeluan desplazatzen dauden bi uhinen ibilbide aldea formula hone bidez adierazten da:

Formulan d, bi zirrikituen arteko distantzia da. Bi uhinak fasean daudenean, hau da, ibilbide desberdintasuna uhin luzerari dagokion zenbaki osoen berdina denean; gehitutako anplitudea eta ondorioz gehitutako intentsitatea maximoa da. Gainera, antifasean daudenean, hau da, ibilbidearen desberdintasuna uhin luzera erdiaren, hiru birenen etab.-en berdina da. Ondoren bi uhinek elkar ezabatzen dute eta gehitutako intentsitatea zero bihurtzen da. Efektu honi interferentzia deritzo; interferentzia maximoa angelu hauetan gertatzen da:
Non λ argiaren uhin luzera den. Banden arteko espazio angeluarra θf :
Zirrikituetatik z distantziara, banden arteko distantzia hau da:
Adibidez, zirrikituen arteko distantzia d=0,5mm eta λ=0,6µm-ko laserraren bidez argiztatzen bada; z=1m-ko distantziara banden arteko distantzia 1,2mm-koa izango da.
b zirrikituaren zabalera uhin luzera baino handiagia bada Fraunhofer difrakzioaren ekuazioak argiaren intentsitate difratatua ematen du:[46]

Non sinc funtzioa x ≠ 0 denean sinc(x)=sin(x)/x den eta x=0 denean sinc(0)=1 den.
Ondoko irudian ikusi dezakegunez, lehenengo patroia zirrikitu bakarraren difrakzio patroia dugu sinc funtzioak emandakoa. Bigarrenean berriz, bi zirrikitutatik difraktaturiko argiaren intentsitate konbinatua ikusi dezakegu; non cos funtzioak egitura bikaina erakusten duen.
Antzeko kalkuluak egin daitezke hurbileko eremuaren Fresnel difrakzioa erabiliz. Behaketa puntua zirrikitura hurbiltzen den einean zirrikitu bakoitzari lotutako difrakzio patroiaren tamainua txikitu egiten da. Honi esker, difrakzioa gertatzen den azalera txikiagotu egiten da eta possible da bi difrakzio patroien gainezarmenik ez dagoen lekuan interferentziak guztiz desagertzea. [47]
Esperimentuen interpretazioak
[aldatu | aldatu iturburu kodea]Copenhageneko interpretazioa
[aldatu | aldatu iturburu kodea]Kopenhageko interpretazioak, mekanika kuantikoaren arloaren aitzindari batzuek proposatuta, baieztatzen du ez dela desiragarria formula matematikoez eta eskala atomikoan gertatzen denaren ezagutza lortzeko aukera ematen duten aparatu fisiko eta erreakzioez harago doan ezer ezartzea. Emaitza esperimental batzuk zehatz iragartzeko aukera ematen duen matematika-egituretako bat probabilitate-uhina deitzen da. Bere forma matematikoan uhin fisiko baten deskribapenaren analogo bat da, baina bere "gailurrak" eta "haranak" zenbait fenomenoren gertaeren probabilitate-mailak adierazten ditu (adibidez, argi-izpi bat une jakin batean detektagailu-pantaila batean), giza esperientzia arruntaren makro-munduan hauteman daitekeena.
Probabilitate-"uhina" "espaziotik igaro dela'' esan daiteke, irudikapen matematikotik kalkula daitezkeen probabilitate-balioak denboraren menpe daudelako. Ezin da partikula baten kokapenaz hitz egin, hala nola fotoi bat emititzen den momentuaren eta detektatzen den denboraren artean, zeren eta, zerbait nonbait kokatuta dagoela esateko, une jakin batean detektatu egin behar baita. Interferentzia-eredu bat agertzeko beharrezkoa da partikulak emititzea, eta partikulak emailetik detektagailura higitzeko gutxienez bi bide ezberdin dituen pantaila bat egotea. Esperimentuek ez dute ezer neurtzen partikularen emisio-denboraren eta detektatzeko pantailara iristearen artean. Izpi baten arrastoa uhin arin bat (fisika klasikoan ulertzen den moduan) bi bideak hartzeko bezain zabala balitz bezala erabiltzen bada, orduan izpi horrek zehazki iragarriko du detektagailuaren pantailan maximo eta minimoak partikula asko aparatutik igarotzen direnean eta pixkanaka espero den interferentzia-eredua "margotuko" du.
Lerro integralen formulazioa
[aldatu | aldatu iturburu kodea]
Kopenhageko interpretazioa Feynmanek emandako mekanika kuantikoaren lerro integralaren formulazioaren antzekoa da. Lerro integralaren formulazioak sistema baterako ibilbide bakar baten nozio klasikoa ordezkatzen du ibilbide guztien gaineko baturarekin. Ibilbideak elkarren artean integrazio funtzionala erabiliz gehitzen dira.
Ibilbide bakoitza era berean gertagarritzat hartzen da eta, beraz, balio berdina gehitzen du. Hala ere, gehiketa horren fasea ibilbidearen edozein puntutan zehar ibilbidearen ekintzak determinatzen du:
Beraz, partikula baten posiziorako probabilitate-banaketa gehiketa horien guztien batuketaren modulua ber bi da,
Probabilitatea kalkulatzean beti gertatzen den bezala, emaitzak normalizatu egin behar dira:
Laburbilduz, emaitzaren probabilitate-banaketa ibilbidearen ekintzarekiko ugalketa proportzionala duten uhinen superposizioaren (hasierako puntutik bukaerako puntura arte dauden ibilbide guztien gainean) modulu normalizatuta ber bi da. Akzio metagarrien aldeak bide ezberdinetan zehar (eta, beraz, gehiketen fase erlatiboek), zirrikitu bikoitzaren saiakuntzaren patroia sortzen dute. Feynmanek azpimarratu zuen bere formulazioa deskribapen matematiko bat besterik ez dela, baina ez da neurtu dezakegun prozesu erreal bat deskribatzeko saiakera bat.
Interpretazio erlatiboa
[aldatu | aldatu iturburu kodea]
Carlo Rovellik proposaturiko mekanika kuantikoaren interpretazio erlatiboaren arabera, zirrikitu bikoitzaren saiakuntzan agertzen diren bezalako behaketak, zehazki, behatzailearen (neurtzeko tresna) eta objektuaren (fisikoki neurtuta) arteko interakzioaren ondorio dira, eta ez objektuaren propietate absolutu batena. Elektroi baten kasuan, hasiera batean "behatu" egiten bada zirrikitu konkretu batean, orduan behatzaile–partikula (fotoi–elektroi) interakzioa elektroiaren kokapenari buruzko informazioa barne hartzen du. Honek partzialki partikula pantailan kokatzea eragozten du. "Behatuta" bada (fotoi baten bidez neurtuta), ez zirrikitu konkretu batean, pantailan baizik, orduan ez dago "zein bidetik" informaziorik interakzioaren barne. Beraz, elektroiak pantailan duen kokapen "behatua" hertsiki determinatzen du bere probabilitate funtzioak. Horrek pantailan sortzen den eredua elektroi bakoitza bi zuloetatik igaro balitz bezalakoa bihurtzen du.
Mundu ugariko interpretazioa
[aldatu | aldatu iturburu kodea]David Deutsch fisikariak bere liburuan "Errealitatearen Prozesua" argudiatzen du zirrikitu bikoitzaren saiakuntza mundu ugariko interpretaziorako ebidentzia dela. Hala ere, mekanika kuantikoaren interpretazio bakoitza enpirikoki bereiztezina denez, zientzialari batzuk eszeptikoak dira.
De Broglie-Bohm teoria
[aldatu | aldatu iturburu kodea]Mekanika kuantikoaren ulermen estandarraren alternatiba bat, De Broglie – Bohm teoriak dio partikulek ere kokapen zehatzak dituztela uneoro, eta abiadura uhin-funtzioaren bidez definitzen dela. Beraz, zirrikitu bikoitzaren saiakuntzan partikula bakar batek zirrikitu konretu bat zeharkatzen duen bitartean, "Uhin pilotu" deritzona bi zirrikituak zeharkatuko ditu. Zirrikitu bikoitzaren de Broglie-Bohm ibilbideak Chris Dewdneyk kalkulatu zituen lehenik, Chris Philippidis eta Basil Hileyrekin, Birkbeck College-n (Londres) lan egiten zuen bitartean. De Broglie-Bohm teoriak mekanika kuantiko estandarraren emaitza estatistiko berberak sortzen ditu, baina bere zailtasun kontzeptual asko sahiesten ditu.
-
Partikulen ibilbidea zirrikitu bikoitzaren saiakuntzan, De Broglie-Bohm teoriaren arabera.
-
100 ibilbide uhin funtzioz gidatuak. De Broglie-Bohm-en teorian, edozein unetan, partikula bat uhin-funtzio eta posizio batez irudikatuta dago (masa zentroa). Hau errealitate areagotua da interpretazio estandarraren aldean.
Erreferentziak
[aldatu | aldatu iturburu kodea]- ↑ a b (Ingelesez) Blog, The Physics arXiv. (2013-11-08). «Physicists Smash Record For Wave-Particle Duality» Medium (Noiz kontsultatua: 2021-02-16).
- ↑ a b (Ingelesez) Physical Chemistry Chemical Physics. 2021-01-02 (Noiz kontsultatua: 2021-02-16).
- ↑ Robinson, Andrew. (2006). The last man who knew everything : Thomas Young, the anonymous polymath who proved Newton wrong, explained how we see, cured the sick, and deciphered the Rosetta stone, among other feats of genius. New York : Pi Press ISBN 978-0-13-134304-7. (Noiz kontsultatua: 2021-02-16).
- ↑ a b c d e (Ingelesez) The Feynman Lectures on Physics. 2021-01-14 (Noiz kontsultatua: 2021-02-16).
- ↑ Charles Sanders Peirce first proposed the use of this effect as an artifact-independent reference standard for length C.S. Peirce (July 1879). "Note on the Progress of Experiments for Comparing a Wave-length with a Meter". American Journal of Science, as referenced by Crease, Robert P. (2011). World in the Balance: The historic quest for an absolute system of measurement. New York: W.W. Norton. p. 317. ISBN 978-0-393-07298-3. p. 203.
- ↑ Greene, B. (Brian). (1999). The elegant universe : superstrings, hidden dimensions, and the quest for the ultimate theory. ISBN 978-0-393-04688-5. (Noiz kontsultatua: 2021-02-16).
- ↑ Feynman, 1965, chapter 3
- ↑ Sir Geoffrey, Ingram Taylor (1909). "Interference Fringes with Feeble Light". Prof. Cam. Phil. Soc. 15: 114.
- ↑ Jönsson, Claus (1 August 1961). "Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten". Zeitschrift für Physik (in German). 161 (4): 454–474. Bibcode:1961ZPhy..161..454J. doi:10.1007/BF01342460. ISSN 0044-3328. S2CID 121659705.
- ↑ Jönsson, Claus (1 January 1974). "Electron Diffraction at Multiple Slits". American Journal of Physics. 42 (1): 4–11. Bibcode:1974AmJPh..42....4J. doi:10.1119/1.1987592. ISSN 0002-9505.
- ↑ Merli, P G; Missiroli, G F; Pozzi, G (1976). "On the statistical aspect of electron interference phenomena". American Journal of Physics. 44 (3): 306–307. Bibcode:1976AmJPh..44..306M. doi:10.1119/1.10184.
- ↑ Rosa, Rodolfo. (2012). «The Merli–Missiroli–Pozzi Two-Slit Electron-Interference Experiment» Physics in Perspective 14 (2): 178–195. doi:. ISSN 1422-6944. PMID 26525832. PMC 4617474. (Noiz kontsultatua: 2021-02-16).
- ↑ "The most beautiful experiment". Physics World 2002 | link is dead.
- ↑ Frabboni, Stefano; Gabrielli, Alessandro; Carlo Gazzadi, Gian; Giorgi, Filippo; Matteucci, Giorgio; Pozzi, Giulio; Cesari, Nicola Semprini; Villa, Mauro; Zoccoli, Antonio (May 2012). "The Young-Feynman two-slits experiment with single electrons: Build-up of the interference pattern and arrival-time distribution using a fast-readout pixel detector". Ultramicroscopy. 116: 73–76. doi:10.1016/j.ultramic.2012.03.017. ISSN 0304-3991.
- ↑ Sala, S.; Ariga, A.; Ereditato, A.; Ferragut, R.; Giammarchi, M.; Leone, M.; Pistillo, C.; Scampoli, P. (2019). "First demonstration of antimatter wave interferometry". Science Advances. 5 (5): eaav7610. Bibcode:2019SciA....5.7610S. doi:10.1126/sciadv.aav7610. PMC 6499593. PMID 31058223.
- ↑ Greene, B.. (2010). The fabric of the cosmos : space, time, and the texture of reality. Vintage eBooks ISBN 978-0-307-42853-0. PMC 681349969. (Noiz kontsultatua: 2021-02-17).
- ↑ a b Donati, O.; Missiroli, G. P.; Pozzi, G.. (1973-05-01). «An Experiment on Electron Interference» American Journal of Physics 41 (5): 639–644. doi:. ISSN 0002-9505. (Noiz kontsultatua: 2021-02-18).
- ↑ a b (Ingelesez) «Quantum wonders: Corpuscles and buckyballs» New Scientist (Noiz kontsultatua: 2021-02-17).
- ↑ (Ingelesez) Nairz, Olaf; Brezger, Björn; Arndt, Markus; Zeilinger, Anton. (2001-09-26). «Diffraction of Complex Molecules by Structures Made of Light» Physical Review Letters 87 (16): 160401. doi:. ISSN 0031-9007. (Noiz kontsultatua: 2021-02-17).
- ↑ (Ingelesez) VCQ. (Noiz kontsultatua: 2021-02-17).
- ↑ (Ingelesez) Nairz, Olaf; Arndt, Markus; Zeilinger, Anton. (2003-04). «Quantum interference experiments with large molecules» American Journal of Physics 71 (4): 319–325. doi:. ISSN 0002-9505. (Noiz kontsultatua: 2021-02-17).
- ↑ Greene, B.. (2004). The fabric of the cosmos : space, time, and the texture of reality. (1st ed. argitaraldia) A.A. Knopf ISBN 0-375-41288-3. PMC 52854030. (Noiz kontsultatua: 2021-02-17).
- ↑ «Complementarity, the Uncertainty Principle, and the Copenhagen Interpretation» Quantum Mechanics (IMPERIAL COLLEGE PRESS): 135–158. 2008-03 ISBN 978-1-86094-977-7. (Noiz kontsultatua: 2021-02-18).
- ↑ «The Copenhagen Interpretation» Understanding Quantum Mechanics (Princeton University Press): 41–54. 2020-12-08 ISBN 978-0-691-22192-2. (Noiz kontsultatua: 2021-02-18).
- ↑ (Ingelesez) Bartell, L. S.. (1980-03-15). «Complementarity in the double-slit experiment: On simple realizable systems for observing intermediate particle-wave behavior» Physical Review D 21 (6): 1698–1699. doi:. ISSN 0556-2821. (Noiz kontsultatua: 2021-02-18).
- ↑ (Ingelesez) Zeilinger, Anton. (1999-03-01). «Experiment and the foundations of quantum physics» Reviews of Modern Physics 71 (2): S288–S297. doi:. ISSN 0034-6861. (Noiz kontsultatua: 2021-02-18).
- ↑ (Ingelesez) Mittelstaedt, P.; Prieur, A.; Schieder, R.. (1987-09). «Unsharp particle-wave duality in a photon split-beam experiment» Foundations of Physics 17 (9): 891–903. doi:. ISSN 0015-9018. (Noiz kontsultatua: 2021-02-18).
- ↑ Greenberger, Daniel M.; Yasin, Allaine. (1988-04). «Simultaneous wave and particle knowledge in a neutron interferometer» Physics Letters A 128 (8): 391–394. doi:. ISSN 0375-9601. (Noiz kontsultatua: 2021-02-18).
- ↑ (Ingelesez) Wootters, William K.; Zurek, Wojciech H.. (1979-01-15). «Complementarity in the double-slit experiment: Quantum nonseparability and a quantitative statement of Bohr's principle» Physical Review D 19 (2): 473–484. doi:. ISSN 0556-2821. (Noiz kontsultatua: 2021-02-18).
- ↑ a b Hillmer, Rachel; Kwiat, Paul. (2007-05). «A Do-It-Yourself Quantum Eraser» Scientific American 296 (5): 90–95. doi:. ISSN 0036-8733. (Noiz kontsultatua: 2021-02-18).
- ↑ a b Chiao, R Y; Kwia, P G; Steinberg, A M. (1995-06). «Quantum non-locality in two-photon experiments at Berkeley» Quantum and Semiclassical Optics: Journal of the European Optical Society Part B 7 (3): 259–278. doi:. ISSN 1355-5111. (Noiz kontsultatua: 2021-02-18).
- ↑ Mittelstaedt, Peter. (1992). «Unsharp Particle—Wave Duality in Double-Slit Experiments» Wave-Particle Duality (Springer US): 169–186. ISBN 978-1-4613-6468-9. (Noiz kontsultatua: 2021-02-18).
- ↑ a b Svensson, Bengt E. Y.. (2013-05-15). «Pedagogical Review of Quantum Measurement Theory with an Emphasis on Weak Measurements» Quanta 2 (1): 18. doi:. ISSN 1314-7374. (Noiz kontsultatua: 2021-02-18).
- ↑ (Ingelesez) Pfleegor, R. L.; Mandel, L.. (1967-07-25). «Interference of Independent Photon Beams» Physical Review 159 (5): 1084–1088. doi:. ISSN 0031-899X. (Noiz kontsultatua: 2021-02-18).
- ↑ (Ingelesez) Sillitto, R.M.; Wykes, Catherine. (1972-05). «An interference experiment with light beams modulated in anti-phase by an electro-optic shutter» Physics Letters A 39 (4): 333–334. doi:. (Noiz kontsultatua: 2021-02-18).
- ↑ (Ingelesez) Arndt, Markus; Nairz, Olaf; Vos-Andreae, Julian; Keller, Claudia; van der Zouw, Gerbrand; Zeilinger, Anton. (1999-10). «Wave–particle duality of C60 molecules» Nature 401 (6754): 680–682. doi:. ISSN 0028-0836. (Noiz kontsultatua: 2021-02-18).
- ↑ (Ingelesez) Schouten, H. F.; Kuzmin, N.; Dubois, G.; Visser, T. D.; Gbur, G.; Alkemade, P. F. A.; Blok, H.; Hooft, G. W. ’t et al.. (2005-02-07). «Plasmon-Assisted Two-Slit Transmission: Young’s Experiment Revisited» Physical Review Letters 94 (5): 053901. doi:. ISSN 0031-9007. (Noiz kontsultatua: 2021-02-18).
- ↑ Bach, Roger; Pope, Damian; Liou, Sy-Hwang; Batelaan, Herman. (2013-03-13). «Controlled double-slit electron diffraction» New Journal of Physics 15 (3): 033018. doi:. ISSN 1367-2630. (Noiz kontsultatua: 2021-02-18).
- ↑ (Ingelesez) Fein, Yaakov Y.; Geyer, Philipp; Zwick, Patrick; Kiałka, Filip; Pedalino, Sebastian; Mayor, Marcel; Gerlich, Stefan; Arndt, Markus. (2019-12). «Quantum superposition of molecules beyond 25 kDa» Nature Physics 15 (12): 1242–1245. doi:. ISSN 1745-2473. (Noiz kontsultatua: 2021-02-18).
- ↑ a b (Ingelesez) Bush, John W.M.. (2015-01-03). «Pilot-Wave Hydrodynamics» Annual Review of Fluid Mechanics 47 (1): 269–292. doi:. ISSN 0066-4189. (Noiz kontsultatua: 2021-03-01).
- ↑ (Ingelesez) Bush, John W. M.. (2010-10-12). «Quantum mechanics writ large: Fig. 1.» Proceedings of the National Academy of Sciences 107 (41): 17455–17456. doi:. ISSN 0027-8424. PMC PMC2955131. (Noiz kontsultatua: 2021-03-01).
- ↑ Natalie Wolchover (30 June 2014). "Have We Been Interpreting Quantum Mechanics Wrong This Whole Time?". Wired.
- ↑ Couder, Y; Fort, E. (2012-05-10). «Probabilities and trajectories in a classical wave-particle duality» Journal of Physics: Conference Series 361: 012001. doi:. ISSN 1742-6596. (Noiz kontsultatua: 2021-03-01).
- ↑ Baggott, Jim (2011). The Quantum Story: A History in 40 Moments. New York: Oxford University Press. pp. 76. ("The wavefunction of a system containing N particles depends on 3N position coordinates and is a function in a 3N-dimensional configuration space or 'phase space'. It is difficult to visualize a reality comprising imaginary functions in an abstract, multi-dimensional space. No difficulty arises, however, if the imaginary functions are not to be given a real interpretation.")
- ↑ (Ingelesez) Li, Pengyun; Sun, Yifan; Yang, Zhenwei; Song, Xinbing; Zhang, Xiangdong. (2016-11). «Classical hypercorrelation and wave-optics analogy of quantum superdense coding» Scientific Reports 5 (1): 18574. doi:. ISSN 2045-2322. PMID 26689679. PMC PMC4686973. (Noiz kontsultatua: 2021-03-01).
- ↑ Jenkins FA and White HE, Fundamentals of Optics, 1967, McGraw Hill, New York
- ↑ Longhurst RS, Physical and Geometrical Optics, 1967, 2nd Edition, Longmans
Ikus, gainera
[aldatu | aldatu iturburu kodea]Kanpo estekak
[aldatu | aldatu iturburu kodea]Animazio interaktiboak
[aldatu | aldatu iturburu kodea]Partikula askeen esperimentua
[aldatu | aldatu iturburu kodea]- Website with the movie and other information from the first single electron experiment by Merli, Missiroli, and Pozzi.
- Movie showing single electron events build up to form an interference pattern in double-slit experiments. Several versions with and without narration (File size = 3.6 to 10.4 MB) (Movie Length = 1m 8s)
- Freeview video 'Electron Waves Unveil the Microcosmos' A Royal Institution Discourse by Akira Tonomura provided by the Vega Science Trust
- Hitachi website that provides background on Tonomura video and link to the video
Hidrodinamiko analogikoak
[aldatu | aldatu iturburu kodea]- "Single-particle interference observed for macroscopic objects"
- Pilot-Wave Hydrodynamics: Supplemental Video
- Through the Wormhole: Yves Couder . Explains Wave/Particle Duality via Silicon Droplets
Ordenagailuko simulazioak
[aldatu | aldatu iturburu kodea]- Java demonstration of Young's double slit interference
- A simulation that runs in Mathematica Player, in which the number of quantum particles, the frequency of the particles, and the slit separation can be independently varied






![{\displaystyle I\propto \cos ^{2}[{\frac {\pi d\sin \theta }{\lambda }}]sinc^{2}[{\frac {\pi b\sin \theta }{\lambda }}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9248a635102aa5f4ccf85bb3ea1240f2bef94762)