Balio absolutu: berrikuspenen arteko aldeak
aurreko edizioan galdutakoak berreskuratu |
No edit summary Etiketak: Ikusizko edizioa Disambiguation links |
||
| 1. lerroa: | 1. lerroa: | ||
[[Category:Pages that use a deprecated format of the math tags]] |
|||
[[Matematika]]n, [[zenbaki erreal]] baten '''balio absolutua''' bere zenbakizko balioa da, zeinua (+ edo -) kontuan hartu gabe. Zenbaki erreal batek zeroraino duen [[distantzia]] ere bada. Adibidez, 3 eta -3 zenbakien balio absolutua 3 da. Kontzeptua beste zenbaki-multzo zenbaitetara zabaldu daiteke, hala nola [[zenbaki konplexu]]etara. |
|||
[[Matematika|Matematikan]], <math>x</math> [[zenbaki erreal]] baten '''balio absolutua''' edo '''modulua'''<ref name="Argand">[[Jean-Robert Argand]], introductor del término ''módulo'' en [[1806]], ver: [http://www.amazon.com/gp/reader/0691027951 Nahin], [http://wvvwhistory.mcs.st-andrews.ac.uk/Mathematicians/Argand.html O'Connor and Robertson], 5- y +5 igual a Cinco y[http://functions.wolfram.com/ComplexComponents/Abs/35/ functions.Wolfram.com.]</ref>, <math>|x|</math> gisan adierazten dena, zeinua kontuan hartu gabe -[[Zenbaki positiboa|positiboa]] nahiz [[Zenbaki negatiboa|negatiboa]]<ref name="va">{{cita libro|apellido=Arias Cabezas|apellido2=Maza Sáez|nombre=José María|nombre2=Ildefonso|año=2008|título=Matemáticas 1|url=|fechaacceso=2 de mayo de 2017|página=16|capítulo=Aritmética y Álgebra|ubicación=Madrid|editorial=Grupo Editorial Bruño, Sociedad Limitada|apellido-editor=Carmona Rodríguez|apellido-editor2=Díaz Fernández|nombre-editor=Manuel|nombre-editor2=Francisco Javier|idioma=español|isbn=9788421659854|número-autores=2}}</ref> izan- zenbaki horrek duen balio ez-negatiboa da. Adibidez, <math>3 |
|||
</math>-ren balio absolutua <math>3 |
|||
</math> da eta <math>-3 |
|||
</math>-ren balio absolutua <math>3 |
|||
</math> da. |
|||
Balio absolutua [[Magnitude fisiko|magnitudearen]], [[Distantzia|distantziaren]] eta [[Norma|normaren]] ideiekin lotuta dago testuinguru matematiko eta fisiko desberdinetan. Zenbaki erreal baten balio absolutuaren kontzeptua beste matematikako objektu askotara orokor daiteke, hala nola, [[Koaternioi|koaternioietara]], [[Eraztun ordenatua|eraztun]] ordenatuetara, [[Gorputz (matematika)|gorputz]] edo [[Bektore espazio|espazio bektorialetara]]. |
|||
== Balio absolutu funtzioa == |
|||
[[Fitxategi:AbsoluteValueDiagram.svg|thumb|Zenbaki baten balio absolutua zerotik zenbaki horretara dagoen distantzia dela pentsa daiteke.]] |
|||
[[Fitxategi:Absolute_value.svg|eskuinera|thumb|230x230px|Balio absolutuaren funtzioaren grafikoa.]] |
|||
== Terminologia eta notazioa == |
|||
[[Fitxategi:Absolute value.svg|thumb|230px|'''Balio absolutu''' funtzioaren grafika.]] |
|||
1806an, [[Jean-Robert Argand]]-ek ''modulu'' terminoa sartu zuen, frantsesez ''neurri-unitatea'' esan nahi duena, bereziki balio absolutu konplexurako<ref name="oed">[[Oxford English Dictionary]], Draft Revision, June 2008</ref><ref>Nahin, [http://www-history.mcs.st-andrews.ac.uk/Mathematicians/Argand.html O'Connor and Robertson], and [http://functions.wolfram.com/ComplexComponents/Abs/35/ functions.Wolfram.com.]; for the French sense, see [[Dictionnaire de la langue française (Littré)|Littré]], 1877</ref>, eta 1866an ingelesean barneratu zuten latinezko ''modulu'' baliokide gisa<ref name="oed" />. ''Balio absolutu'' terminoa, gutxienez, 1806tik erabili da frantsesez<ref>{{Erreferentzia|izenburua=Lazare Nicolas Marguerite Carnot|hizkuntza=eu|data=2020-12-30|url=https://eu.wikipedia.org/w/index.php?title=Lazare_Nicolas_Marguerite_Carnot&oldid=8316402|sartze-data=2021-11-03|encyclopedia=Wikipedia, entziklopedia askea.}}</ref> eta 1857tik ingelesez<ref>{{Erreferentzia|abizena=James Mills Peirce|izenburua=A Text-book of Analytic Geometry: On the Basis of Professor Peirce's Treatise|argitaletxea=J. Bartlett|hizkuntza=English|data=1857|url=http://archive.org/details/atextbookanalyt00peirgoog|sartze-data=2021-11-03}}</ref>. Alde bakoitzeko barra bertikal |x| notazioa [[Karl Weierstrass]]-ek sartu zuen 1841ean<ref>{{Erreferentzia|izena=Nicholas J.|abizena=Higham|izenburua=Handbook of writing for the mathematical sciences|data=2020|url=https://www.worldcat.org/oclc/1131865104|edizioa=Third edition|isbn=978-1-61197-609-0|pmc=1131865104|sartze-data=2021-11-03}}</ref>. ''Balio absoluturako'' beste termino batzuk ''zenbakizko balioa<ref name="oed" />'' eta ''magnitudea'' izan daitezke<ref name="oed" />. Programazio-hizkuntzetan eta software konputazionaleko paketeetan, x-ren balio absolutua abs(x) edo antzeko adierazpen baten bidez adierazten da. |
|||
Barra bertikaletako idazkera beste zenbait testuinguru matematikotan ere agertzen da: adibidez, multzo bati aplikatzean, bere [[Kardinalitate|kardinala]] adierazten du; [[matrize]] bati aplikatzen zaionean, bere [[Determinante|determinantea]] adierazten du. Barra bertikalek balio absolutua adierazten dute balio absolutua definituta dagoen objektu aljebraikoetarako soilik, bereziki [[Zatiketa arautuaren aljebra|zatiketa normatu aljebraikoaren]] elementu baterako, adibidez, zenbaki erreal baterako, zenbaki konplexu baterako edo kuaternioi baterako. Barra bertikalen erabilera <math>\R^n</math>-ko bektore baten [[Euklidear espazio|norma euklidear]] <ref>{{Erreferentzia|izena=Michael|abizena=Spivak|izenburua=Calculus on manifolds : a modern approach to classical theorems of advanced calculus|data=1965|url=https://www.worldcat.org/oclc/187146|isbn=0-8053-9021-9|pmc=187146|sartze-data=2021-11-03}}</ref>eta [[Sup araua|goi normarako]]<ref>{{Erreferentzia|izena=James R.|abizena=Munkres|izenburua=Analysis on manifolds|argitaletxea=Addison-Wesley Pub. Co., Advanced Book Program|data=1991|url=https://www.worldcat.org/oclc/170966279|isbn=978-1-4294-8504-3|pmc=170966279|sartze-data=2021-11-03}}</ref>, oso erlazionatuta dagoen baina desberdina den notazioa da, nahiz eta azpiindizedun barra bertikal bikoitzak ( <math>\|\cdot\|_2</math> eta <math>\|\cdot\|_\infty</math>, hurrenez hurren) notazio arruntagoak eta ez hain anbiguoak diren. |
|||
'''x''' zenbaki erreal baten balio absolutua honela adierazten da: '''|x|'''. Analitikoki, honela definitzen da funtzioa: |
|||
== Definizioa == |
|||
:<math>f(x)=|x| = \begin{cases} |
|||
\;\;\;x, & x \ge 0\ \ \mbox{bada }\\ |
|||
-x, & x < 0\ \ \mbox{bada } |
|||
\end{cases} </math> |
|||
=== Zenbaki errealak === |
|||
== Balio absolutua zenbaki konplexuetan == |
|||
Edozein <math>x</math> zenbaki errealen '''balio absolutua''' edo '''modulua,''' honela adierazten da: <math>|x|</math> eta modu honetan definitzen da:<ref>Dolciani y otros. ''álgebra moderna''</ref> |
|||
<math>|x|= |
|||
[[Fitxategi:Complex_conjugate_picture.svg|eskuinera|thumb| <math>z</math> zenbaki konplexu baten balio absolutua <math>z</math>-tik jatorrira dagoen <math>r</math> distantzia da. Irudian, <math>z</math> eta bere [[Konjugatu (matematika)|konjugatu konplexua]] <math>\bar z</math> balio absolutu bera dutela ere ikus daiteke. ]] |
|||
\left\{ |
|||
[[Zenbaki konplexu|Zenbaki konplexuak]] ez daudenez ordenatuta, goian emandako zenbaki errealentzako balio absolutuaren definizioa ezin zaie zuzenean aplikatu zenbaki konplexuei. Hala ere, zenbaki erreal baten balio absolutuaren interpretazio geometrikoa 0tik bere distantziara orokor daiteke. Zenbaki konplexu baten balio absolutua [[Plano konplexu|plano konplexuan]] [[Jatorri (geometria)|dagokion puntutik jatorriraino]] dagoen distantzia euklidearrak definitzen du. Hau, [[Pitagorasen teorema]] erabiliz kalkula daiteke: edozein zenbaki konplexutarako |
|||
\begin{array}{rcl} |
|||
x, & \mbox{baldin eta} & x \geq 0 \\ |
|||
-x, & \mbox{baldin eta} & x < 0 |
|||
\end{array} |
|||
\right.</math> |
|||
<math>x</math>-ren balio absolutua beti da zenbaki positiboa edo [[zero]], baina inoiz ez negatiboa: zenbaki negatiboa denean <math>(x<0)</math>, haren balio absolutua nahitaez positiboa da <math>(|x|=-x>0)</math>. |
|||
: <math>z = x + iy,</math> |
|||
Ikuspuntu geometrikotik, zenbaki erreal baten balio absolutua zenbaki horren eta zeroaren artean dagoen distantzia bezala ikus daiteke. Oro har, bi zenbakiren arteko aldearen balio absolutua haien arteko distantzia da. |
|||
non {{Mvar|x}} eta {{Mvar|y}} zenbaki errealak diren, {{Mvar|z}}-ren '''balio absolutua''' edo '''modulua''' | z | ikurraren bidez adierazten da eta honela definitzen da |
|||
=== Propietateak === |
|||
: <math>|z| = \sqrt{[\operatorname{Re}(z)]^2 + [\operatorname{Im}(z)]^2}=\sqrt{x^2 + y^2},</math> |
|||
Balio absolutuak funtsezko lau propietate hauek ditu, <math>a,b\in\mathbb{R} |
|||
</math> izanik: |
|||
<math>\begin{align} |
|||
non Re ''(z)'' = ''x'' eta Im ''(z)'' = ''y'' ''z'' -ren zati erreala eta irudikaria diren, hurrenez hurren. {{Mvar|y}} zati irudikaria zero denean, hau bat dator {{Mvar|x}} zenbaki errealaren balio absolutuaren definizioarekin. |
|||
&|a|\geq0 & \text{Ez-negatibotasuna} \\ |
|||
&|a|=0\iff a=0 & \text{Positiboki definitua} \\ |
|||
&|ab|=|a||b| & \text{Propietate biderkakorra} \\ |
|||
&|a+b|\leq|a|+|b| & \text{Desberdintza triangeluarra} |
|||
\end{align} |
|||
</math> |
|||
Beste propietate erabilgarri batzuk ondoko hauek dira: |
|||
{{Mvar|z}} zenbaki konplexua [[Zenbaki konplexu|bere forma polarrean]] honela adierazten da |
|||
<math>\begin{align} |
|||
&||a||=|a| \\ |
|||
&|-a|=|a| \\ |
|||
&|a-b|=0 \iff a=b \\ |
|||
&|a-b|\leq|a-c|+|c-b| \\ |
|||
&\left|\frac{a}{b}\right|=\frac{|a|}{|b|}\quad\text{baldin }b\neq0 \\ |
|||
&|a-b|\geq||a|-|b|| |
|||
\end{align} |
|||
</math> |
|||
horiek definizioaren edo lehenengo lau propietateen ondoriok dira. |
|||
non <math display="inline">r = \sqrt{[\operatorname{Re}(z)]^2 + [\operatorname{Im}(z)]^2} \ge 0</math> (eta θ ∈ arg (z) z-ren [[Argumentu (analisi konplexua)|argumentua]] (edo fasea)) , bere balio absolutua honakoa da |
|||
Desberdintasunak erabiltzen dituzten beste bi propietate, ondokoak dira: |
|||
: <math>|z| = r .</math> |
|||
<math>\begin{align} |
|||
Edozein {{Mvar|z}} zenbaki konplexuren eta balio absolutu bera duen bere [[Konjugatu (matematika)|konjugatu konplexuaren]] {{Nowrap|<math>\bar z = x - iy</math>,}} arteko produktua, <math>\left(x^2 + y^2\right)</math> zenbaki erreal ez-negatiboa da beti, {{Mvar|z}} zenbaki konplexu baten balio absolutua <math>z \cdot \overline{z}</math>produktuaren erro karratua da, horregatik {{Mvar|z}} karratu absolutua edo ''karratu modulua'' deritzo: |
|||
&|a|\leq b \iff -b\leq a\leq b \\ |
|||
&|a|\geq b \iff a\leq -b\quad\mbox{ edo }\quad a\geq b |
|||
\end{align}</math> |
|||
Erlazio horiek balio absolutua duten desberdintasunak ebazteko erabil daitezke, adibidez: |
|||
: <math>|z| = \sqrt{z \cdot \overline{z}}.</math> |
|||
<math>\begin{align} |
|||
<nowiki>Honek zenbaki errealentzako definizio alternatiboa orokortzen du: {\textstyle |x|={\sqrt {x\cdot x}}}</nowiki> |
|||
|x-3|\leq 9 |
|||
&\iff -9\leq x-3\leq 9 \\ |
|||
&\iff -6\leq x\leq 12 |
|||
\end{align}</math> |
|||
=== Zenbaki konplexuak === |
|||
{{nowrap|<math display="inline">|x| = \sqrt{x\cdot x}</math>.}} |
|||
[[Zenbaki konplexu|Zenbaki konplexuak]] ez daudenez ordenatuta, zenbaki errealentzat emandako balio absolutuaren definizioa ezin zaie zuzenean aplikatu. Hala ere, zenbaki erreal baten balio absolutuaren interpretazio geometrikoa 0tik bere distantziara orokor daiteke. Eta beraz, zenbaki konplexu baten balio absolutua [[Plano konplexu|plano konplexuan]] dagokion puntutik jatorriraino dagoen distantzia euklidearrak definitzen du. Hau [[Pitagorasen teorema]] erabiliz kalkula daiteke: edozein zenbaki konplexutarako. |
|||
[[Fitxategi:Complex_conjugate_picture.svg|eskuinera|thumb| <math>z</math> zenbaki konplexu baten balio absolutua <math>z</math>-tik jatorrira dagoen <math>r</math> distantzia da. Irudian, <math>z</math> eta bere [[Konjugatu (matematika)|konjugatu konplexua]] <math>\bar z</math> balio absolutu bera dutela ere ikus daiteke.]] |
|||
<math> z=x+iy</math> |
|||
non <math> x</math> eta <math> y</math> zenbaki errealak diren, <math> z</math> -ren '''balio absolutua''' edo '''modulua''' <math> |z|</math> ikurraren bidez adierazten da eta honela definitzen da<ref>{{Erreferentzia|izena=Mario O.|abizena=González|izenburua=Classical complex analysis|argitaletxea=M. Dekker|data=1992|url=https://www.worldcat.org/oclc/45728566|isbn=0-585-31691-0|pmc=45728566|sartze-data=2021-11-03}}</ref>: |
|||
Zenbaki konplexuentzako balio absolutuak, goian aipatutako zenbaki errealen balio absolutuarentzako emandako oinarrizko lau propietateak partekatzen ditu. |
|||
<math> |z|=\sqrt{|Re(z)|^2+|Im(z)|^2}=\sqrt{x^2+y^2}</math>, |
|||
Talde-teoriaren hikuntzan, biderkatze propietatea hurrengo moduan berridatz daiteke: balio absolutua zenbaki konplexuen biderkatze-taldetik zenbaki erreal positiboen biderkatze-taldera doan homomorfismo-talde bat da. |
|||
non <math> Re(z)=x</math> eta <math> Im(z)=y</math> <math> z</math>-ren zati erreala eta irudikaria diren, hurrenez hurren. <math> y</math> zati irudikaria 0 denean, hau bat dator <math> x</math> zenbaki errealaren balio absolutuaren definizioarekin. |
|||
Subaditibitatearen propietatea ("desberdintza triangeluar konplexua") n zenbaki konplexu dituen (chorongo) edozein bilduma finitura honela hedatzen da: {{NumBlk|:|<math>\left| \sum_{k=1}^n z_k\right| \leq \sum_{k=1}^n \left|z_k\right| . </math>|{{EquationRef|⁎}}}}Desberdintasun hau familia infinituetan ere aplikatzen da, baldin eta <math display="inline">\sum_{k=1}^\infty z_k</math> serie infinitua erabat konbergentea bada . Lebesgueren integrazioa batuketaren analogia jarraitutzat hartzen bada, <math>f: \R \to \C</math> funtzio neurgarriak E azpimultzo neurgarri batean integratuta daudenean, desberdintasun hau balio konplexuaren bidez analogikoki betetzen da. Ideia honela adieraz daiteke:{{NumBlk|:|<math>\left|\int_E f\, dx\right| \leq \int_E \left|f\right| dx. </math>|{{EquationRef|⁎⁎}}}}[[Riemannen integral|(Honek Riemann-en]] funtzio integragarriak <math>[a,b]</math> tarte mugatu baten barnean sartzen ditu, kasu berezi gisa. ) |
|||
<math> z</math> zenbaki konplexua bere [[Koordenatu polar|forma polarrean]] honela adierazten da: |
|||
==== Desberdintza triangeluar konplexuaren froga ==== |
|||
Desberdintza triangeluarrak, ( {{EkuazioOhar|⁎}} ) -k emanda, erraz egiaztatutako zenbaki konplexuen hiru propietate aplikatuta froga daiteke. Hots, <math>z \in \Complex</math>zenbaki konplexu bakoitzerako, |
|||
<math> z=re^{i\theta}</math>, |
|||
[[Category:Pages that use a deprecated format of the math tags]] |
|||
non <math> r=\sqrt{|Re(z)|^2+|Im(z)|^2}\geq0</math> (eta <math> \theta\in arg(z)</math> <math> z</math>-ren [[Argumentu (analisi konplexua)|argumentua]] (edo fasea)), bere balio absolutua honakoa da: |
|||
<math> |z|=r</math>. |
|||
Edozein <math> z</math> zenbaki konplexuren eta balio absolutu bera duen bere [[Konjugatu (matematika)|konjugatu]] konplexuaren <math> \bar{z}=x-iy</math> arteko produktua, (<math> x^2+y^2</math>) zenbaki erreal ez-negatiboa da beti. Gainera, <math> z</math> zenbaki konplexu baten balio absolutua <math> z\cdot\bar{z}</math> produktuaren erro karratua da, horregatik, <math> z</math> [[karratu absolutua]] edo karratu modulua deritzo: |
|||
<math> |z|=\sqrt{z\cdot\bar{z}}</math>. |
|||
Honek zenbaki errealentzako definizio alternatiboa orokortzen du: <math> |x|=\sqrt{x\cdot{x}}</math> |
|||
Zenbaki konplexuentzako balio absolutuak, goian zenbaki errealen balio absolutuarentzat emandako oinarrizko lau propietateak partekatzen ditu. |
|||
[[Talde-teoria]]<nowiki/>ren hizkuntzan, biderkatze propietatea hurrengo moduan berridatz daiteke: balio absolutua da zenbaki konplexuen [[Biderkatze-taldea|biderkatze-taldetik]] [[zenbaki erreal positibo]]<nowiki/>en biderkatze-taldera doan [[homomorfismo-talde]] bat<ref>{{Erreferentzia|izena=Falko|abizena=Lorenz|izenburua=Algebra|argitaletxea=Springer|data=2006-2008|url=https://www.worldcat.org/oclc/209914197|isbn=978-0-387-31608-6|pmc=209914197|sartze-data=2021-11-03}}</ref>. |
|||
[[Subaditibitate|Azpigehigarritasunaren]] propietatea ("[[Desberdintza triangeluarra|desberdintza triangeluar]] konplexua") <math> n</math> zenbaki konplexu dituen <math display="inline">(z_k)_{k=1}^n </math> edozein bilduma finitura honela hedatzen da: |
|||
<math> \left\vert \sum_{k=1}^n z_{k} \right\vert \leq \sum_{k=1}^n |z_{k}|.</math> (*) |
|||
Desberdintasun hau familia infinituetan ere aplikatzen da, baldin eta <math display="inline">\sum_{k=1}^\infty z_k</math> serie infinitua erabat konbergentea bada. Lebesgueren integrazioa batuketaren analogia jarraitutzat hartzen bada, <math>f: \R \to \C</math> funtzio neurgarriak <math> E</math> azpimultzo batean integratuta daudenean, desberdintasun hau balio konplexuaren bidez analogikoki betetzen da. Ideia hau honela adieraz daiteke: |
|||
<math> \left\vert \int_{E}^{} fdx \right\vert\leq \int_{E}^{} \left\vert f\right\vert dx</math> (**) |
|||
(Honek Riemann-en funtzio integragarriak <math> [a,b]</math> tarte mugatu baten barnean sartzen ditu, kasu berezi gisa). |
|||
=== Desberdintza triangeluar konplexuaren froga === |
|||
Desberdintza triangeluarra, (*) -k emanda, zenbaki konplexuen hiru propietate aplikatuta froga daiteke. Hots, <math>z \in \Complex</math> zenbaki konplexu bakoitzerako: |
|||
# Existitzen da <math> c \in \Complex</math> zeinetarako <math>|c|=1</math> eta <math>|z|=c \cdot z</math>; |
|||
# <math>\operatorname{Re}(z)\leq |z|</math> |
|||
Gainera, {{Nowrap|<math>(w_k)_{k=1}^{n}</math>,}} zenbaki konplexuen edozein familiarentzat {{Nowrap|<math display="inline">\sum_k w_k = \sum_k \operatorname{Re} (w_k) + i \sum_k \operatorname{Im} (w_k)</math>}} betetzen da. Zehazki, |
|||
3. <math display="inline">\sum_k w_k \in \R</math> bada, orduan <math display="inline">\sum_k w_k =\sum_k \operatorname{Re} (w_k)</math>. |
|||
(*)-ren froga: aukeratu <math>c \in \C</math> zeinetarako |c|=1 eta <math display="inline">\left|\sum_k z_k\right| = c \left(\sum_k z_k\right)</math> betetzen diren. Ondorengo kalkuluak bilatzen ari garen desberdintza ematen digu: <math>\left|\sum_k z_k\right|\; \overset{(1)} {=}\; c\left(\sum_k z_k\right) = \sum_k cz_k\; \overset{(3)} {=}\;\sum_k\operatorname{Re}(cz_k)\; \overset{(2)} {\le}\; \sum_k |cz_k| = \sum_k \left|c\right| \left|z_k\right| = \sum_k \left| z_k \right| .</math> |
|||
Froga honi esker, argi dago (*) berdintasuna betetzen dela, baldin eta <math>c z_k</math> zenbaki erreal ez-negatiboak badira, eta, aldi berean, zeroren ezberdinak diren <math>z_k</math> guztiek argumentu bera badute. Hau da, <math>z_k = a_k\zeta</math> da, <math>\zeta</math> konstante konplexu baterako eta <math>a_k \geq 0</math> konstante erreal baterako, non {{Nowrap|<math>1 \le k \le n</math>.}} den. |
|||
{{Nowrap|<math>f</math>}} neurgarria izateak <math> |f|</math> neurgarria izatea inplikatzen duenez, (**) desberdintzaren froga teknika bera erabiliz burutzen da, <math display="inline">\sum_k(\cdot)</math> adierazpena <math display="inline">\int_E (\cdot)\, dx</math> -rekin eta <math>z_k</math> adierazpena {{Nowrap|<math>f(x)</math>}}-rekin ordezkatuz<ref>{{Erreferentzia|izena=Walter|abizena=Rudin|izenburua=Principles of mathematical analysis|data=1976|url=https://www.worldcat.org/oclc/1502474|edizioa=Third edition|isbn=0-07-054235-X|pmc=1502474|sartze-data=2021-11-03}}</ref>. |
|||
=== Definizio baliokidea === |
|||
<math> x </math> zenbaki erreala bada, haren balio absolutua zenbaki erreal ez-negatibo bat da, honela definitua dagoena: |
|||
# <math> |x|= \sqrt{x^2}</math> |
|||
# <math> |x| </math>, <math>\{-x,x\}</math><ref>Spivak. Calculus I</ref> hauen arteko maximoaren berdina da. |
|||
== Balio absolutuaren funtzioa == |
|||
[[Fitxategi:Función_Cu_abs.svg|eskuinera|280x280px]] |
|||
Zenbaki errealen balio absolutu funtzioa zenbaki erreal guztien multzoaren gainean definitzen da, zenbaki erreal bakoitzari bere balio absolutua emanez. |
|||
Formalki, <math>x\,</math> zenbaki erreal guztien ''balio absolutua'' honela definitzen da:<ref name="Wolfram">[http://functions.wolfram.com/ComplexComponents/Abs/35/ functions.Wolfram.com] introducción de la notación <math>|x|</math>, por [[Karl Weierstrass]] en [[1841]].</ref> |
|||
<math> \begin{align} |
|||
|\quad| :\mathbb{R} &\to\mathbb{R}^{+}\cup\{0\} \\ |
|||
x&\mapsto|x| |
|||
\end{align} </math> |
|||
eta honela adierazten da: |
|||
<math>\text{abs}(x) = |x| = \left \{ |
|||
\begin{array}{rcl} |
|||
x, & \mbox{baldin} & x \ge 0 \\ |
|||
-x, & \mbox{baldin} & x < 0 |
|||
\end{array} \right. |
|||
</math> |
|||
Definizioz, <math> x \, </math>-ren balio absolutua beti zero edo zero baino handiagoa izango da, eta inoiz ez negatiboa. |
|||
* ''Balio absolutu funtzioa'' [[funtzio jarraitu]] bat da zuzen erreal osoan; bere deribatuak etena du (0;0) puntuan, balio konstanteko bi adar baitaude. Hau da, funtzio hori diferentziagarria da R osoan, x=0 puntuan izan ezik. |
|||
* <math>y=x \left\vert x \right\vert</math> funtzioa, balio absolutua erabiliz, funtzio gorakorra eta jarraitua da; bere grafikoa parabolaren grafikotik lortzen da <math>y=x^2</math>, ezkerreko adarra <math>O x</math> ardatzarekiko islatuz. |
|||
Errealen multzoa balio absolutuak definitutako arauarekin, [[Banach espazioa|Banach espazio]] bat da<math>(\R,|\cdot|)</math>. |
|||
=== Zeinu-funtzioarekiko erlazioa === |
|||
Zenbaki errealen balio absolutu funtzioak bere balioa itzultzen du zeinua kontuan hartu gabe; [[zeinu funtzioak]], berriz, zenbaki baten zeinua itzultzen du, haren balioa kontuan hartu gabe. Ekuazio hauek bi funtzio horien arteko erlazioa erakusten dute: |
|||
<math> |x|=x\operatorname{sgn}(x) </math>, <math> x= 0 </math> den kasurako |
|||
edo |
|||
<math> |x|\operatorname{sgn}(x)=x </math> |
|||
eta <math> x\neq 0 </math> kasuan, |
|||
<math> \operatorname{sgn}(x)=\frac{|x|}{x}=\frac{x}{|x|} </math> |
|||
=== Deribatua === |
|||
Balio absolutu funtzioak [[deribatu]] bat du <math> x\neq0 </math> bakoitzerako, baina ez da diferentziagarria <math> x=0 </math> kasuan. <math> x\neq0 </math> kasuan, aldiz, deribatua honako funtzio honek ematen du<ref>{{Erreferentzia|izena=Eric W.|abizena=Weisstein|izenburua=Absolute Value|hizkuntza=en|url=https://mathworld.wolfram.com/AbsoluteValue.html|aldizkaria=mathworld.wolfram.com|sartze-data=2021-11-03}}</ref><ref>{{Erreferentzia|izena=Robert G.|abizena=Bartle|izenburua=Introduction to real analysis|argitaletxea=Wiley|data=1982|url=https://www.worldcat.org/oclc/7875643|isbn=0-471-05944-7|pmc=7875643|sartze-data=2021-11-03}}</ref>: |
|||
<math> \frac{d}{dx}|x|=\frac{x}{|x|} |
|||
= |
|||
\begin{cases} |
|||
-1 & x<0 \\ |
|||
1 & x>0 |
|||
\end{cases} </math> |
|||
[[Fitxategi:Absolute_value_composition.svg|thumb|332x332px|Balio absolutuaren [[Funtzioen konposaketa|osaera]] ordena ezberdinetako [[funtzio kubiko]] batekin.]] |
|||
=== Antideribatua === |
|||
[[Zenbaki errealen balio absolutuaren funtzioaren integral mugagabea|Zenbaki errealen balio absolutu funtzioaren integral mugagabea]] hurrengoa da: |
|||
<math> \int |x|dx=\frac{x|x|}{2}+C </math> |
|||
non <math> C </math> integrazio arbitrario [[Integrazio-konstante|konstantea]] den. |
|||
== Distantzia == |
|||
Balio absolutuak lotura estua du distantziaren ideiarekin. Lehen esan bezala, zenbaki erreal edo konplexu baten balio absolutua, zenbaki horrek jatorrira duen distantzia da; zenbaki errealetarako, zenbaki errealen zuzenean zehar, eta zenbaki konplexuetarako, plano konplexuan. Eskuarki, bi zenbaki errealen edo konplexuen arteko diferentziaren balio absolutua, bi zenbaki errealen edo konplexuen arteko distantzia da. |
|||
Bi <math>a = (a_1, a_2, \dots, a_n) </math> eta <math>b = (b_1, b_2, \dots, b_n) </math> punturen arteko [[Distantzia euklidearra|distantzia euklidear]] estandarra [[Euklidear espazio|{{Mvar|n}} -espazio euklidearrean]] honela definitzen da: |
|||
<math>\sqrt{\textstyle\sum_{i=1}^n(a_i-b_i)^2}. </math> |
|||
Hau orokortze gisa ikus daiteke, izan ere <math>a_1</math> eta <math>b_1</math> errealentzat , hau da, dimentsio baten, balio absolutuaren definizio alternatiboaren arabera, honako adierazpena dugu: |
|||
<math>|a_1 - b_1| = \sqrt{(a_1 - b_1)^2} = \sqrt{\textstyle\sum_{i=1}^1(a_i-b_i)^2},</math> |
|||
eta <math> a = a_1 + i a_2 </math> eta <math> b = b_1 + i b_2 </math> zenbaki konplexuentzat , hau da, bi dimentsiotan, honako hau: |
|||
{| |
|||
|<math>|a - b| </math> |
|||
|<math> = |(a_1 + i a_2) - (b_1 + i b_2)|</math> |
|||
|- |
|||
| |
|||
|<math> = |(a_1 - b_1) + i(a_2 - b_2)|</math> |
|||
|- |
|||
| |
|||
|<math> = \sqrt{(a_1 - b_1)^2 + (a_2 - b_2)^2} = \sqrt{\textstyle\sum_{i=1}^2(a_i-b_i)^2}.</math> |
|||
|} |
|||
Aurrekoak erakusten du "balio absolutu"-distantzia, bat datorrela distantzia euklidear estandarrarekin, zenbaki errealentzat eta konplexuentzat. Zeintzuk oinordetzan hartzen dituzten, dimentsio bakarreko eta bi dimentsioko espazio euklidear gisa hartzearen ondorioz, hurrenez hurren. |
|||
Bi zenbaki erreal edo konplexuren diferentziaren balio absolutuaren propietateek: ez-negatibotasunak, bereizezinen identitateak, simetriak eta goian adierazitako desberdintza triangeluarrak, [[Metrika (matematika)|distantzia-funtzioaren]] ideia orokorragoa bultzatzen dutela ikus daiteke: |
|||
X × X multzoko d funtzio erreal bati {{Mvar|X}}-ko [[metrika]] (edo ''distantzia funtzioa'' ) deitzen zaio lau axioma hauek betetzen baditu: |
|||
{| |
|||
|<math>d(a, b) \ge 0 </math> |
|||
|<math>\text{Ez-negatibotasuna} |
|||
</math> |
|||
|- |
|||
|<math>d(a, b) = 0 \iff a = b </math> |
|||
|<math>\text{Bereiztezinen identitatea} |
|||
</math> |
|||
|- |
|||
|<math>d(a, b) = d(b, a) </math> |
|||
|<math>\text{Simetria} |
|||
</math> |
|||
|- |
|||
|<math>d(a, b) \le d(a, c) + d(c, b) </math> |
|||
|<math>\text{Desberdintza triangeluarra} |
|||
</math> |
|||
|} |
|||
== Orokortzeak == |
|||
=== Zenbaki hiperkonplexuak === |
|||
Zenbaki konplexuetan ez ezik, balio absolutuaren funtzioa [[Zenbaki hiperkonplexu|zenbaki hiperkonplexuetara]] ere orokor daiteke, hala nola, kuaternioietara edo oktonioietara. [[Gorputz baten gaineko aljebra|Zenbaki errealen gaineko aljebra]]<nowiki/>n, h zenbaki baten balio absolutua honela definitzen da: |
|||
<math>\left\vert h \right\vert=\sqrt{ h \bar{h}} |
|||
</math> |
|||
Non <math>\bar{h}</math> <math>h</math>-ren [[Hiperkonjugazio|hiperkonjugazioa]] den. |
|||
=== Eraztun ordenatuak === |
|||
Goian aipatutako zenbaki errealetarako emandako balio absolutuaren definizioa edozein eraztun ordenatutara heda daiteke. Hau da, a <math>\in \mathbb{R}</math> eraztun ordenatuaren elementu bat baldin bada, a-ren balio absolutua, |a| bidez adierazten dena, honela definitzen da<ref>{{Erreferentzia|izena=Saunders Mac|abizena=Lane|izenburua=Algebra|argitaletxea=American Mathematical Soc.|hizkuntza=en|abizena2=Birkhoff|izena2=Garrett|data=1999|url=https://books.google.es/books?id=L6FENd8GHIUC&pg=PA264&redir_esc=y#v=onepage&q&f=false|isbn=978-0-8218-1646-2|sartze-data=2021-11-03}}</ref>: |
|||
<math>|a| = \left\{ |
|||
\begin{array}{rl} |
|||
a, & \text{baldin } a \geq 0 \\ |
|||
-a, & \text{baldin } a < 0. |
|||
\end{array}\right. |
|||
</math> |
|||
non −a, a-ren alderantzizko gehigarria den, 0 identitate gehigarria den, eta < eta ≥ ikurrek eraztuneko ordenamenduari dagokion ohiko esanahia duten. |
|||
=== Espazio bektorialak === |
|||
Artikulu nagusia: Norma (matematika) |
|||
Zenbaki errealen balio absolutuaren oinarrizko propietateak, espazio bektorial arbitrario batera orokortzeko erabil daitezke, aldaketa txiki bat eginez. |
|||
F eremu baten gaineko V [[Bektore espazio|espazio bektorial]] batean, balio errealeko funtzioari '''balio absolutua''' deritzo, || · || gisa adierazten dena. Baina, honako axioma hauek betetzen baditu, norma deitzen zaio: |
|||
F-ko a guztietarako eta V-ko '''u,v''' guztietarako, |
|||
{| |
|||
|+ |
|||
|<math>||\textbf{v}|| \geq 0 |
|||
</math> |
|||
|<math>\text{Ez-negatibotasuna} |
|||
</math> |
|||
|- |
|||
|<math>||\textbf{v}||=0 \Longleftrightarrow \textbf{v}=0 |
|||
</math> |
|||
|<math>\text{Positiboki definitua} |
|||
</math> |
|||
|- |
|||
|<math>||a\textbf{v}||= |a| ||\textbf{v}|| |
|||
</math> |
|||
|<math>\text{Homogeneotasun positiboa edo eskalagarritasun positiboa} |
|||
</math> |
|||
|- |
|||
|<math>|| \textbf{v} + \textbf{u}|| \leq || \textbf{v}|| + || \textbf{u}|| |
|||
</math> |
|||
|<math>\text{Azpigehigarritasuna edo desberdintza triangeluarra} |
|||
</math> |
|||
|} |
|||
Bektore baten norma, magnitude edo luzera izenarekin ere ezaguna da. |
|||
<math>\mathbb{R}^n</math>espazio euklidearraren kasuan, honela definitutako funtzioari |
|||
<math>\|(x_1, x_2, \dots, x_n) \| = \sqrt{\textstyle\sum_{i=1}^{n} x_i^2}</math> |
|||
[[norma euklidearra]] deritzo. <math>\mathbb{R}</math> zenbaki errealak dimentsio bakarreko <math>\mathbb{R}^1</math> espazio bektorialtzat hartzen direnean, balio absolutua [[p-norma]] da, (ikusi [[Lp espazioa|L<sup>p</sup> espazioa]]) edozein p-rentzat. Izan ere, balio absolutua norma "bakarra" da, zentzu honetan, <math>\mathbb{R}^1</math>-eko <math>|| \cdot || |
|||
</math> norma guztietarako, <math>||x||= ||1|| \cdot |x| |
|||
</math> betetzen da. |
|||
Balio absolutu konplexua, [[barne produktu-espazio]] bateko normaren kasu berezi bat da. Balio absolutu hau, norma euklidearraren berdina da plano konplexua <math>\mathbb{R}^2</math>-ko [[plano euklidear]] gisa identifikatzen denean. |
|||
=== Konposaketa aljebraikoak === |
|||
A konposaketa aljebraiko orok bere '''konjugazio''' izena hartzen duen ''x → x*'' [[Inboluzio (argipena)|inboluzioa]] du. A-n, x elementu baten eta ''x*'' elementu horren konjokatuaren arteko produktuari, ''x'' elementuaren '''norma''' deritzo eta era honetan adierazten da: ''N(x) = x x*''. |
|||
<math>\mathbb{R}</math> zenbaki errealak, <math>\C</math> zenbaki konplexuak eta <math>\H</math> kuaternioiak [[forma koadratiko]] zehatzek emandako normak dituzten konposaketa aljebraikoak dira. [[Zatiketa-aljebra]] horietan, balio absolutua, aljebraren normaren konposizioaren [[erro karratu]]<nowiki/>ak ematen du. |
|||
Orokorrean, konposaketa aljebraikoaren norma definitu gabeko forma koadratikoa izan daiteke eta [[bektore nuluak]] ditu. Hala ere, zatiketa-aljebren kasuan bezala, ''x'' elementu batek zero ez den norma duenean, orduan ''x-''k ''x*/N (x)'' -k emandako [[Alderantzizko zenbaki|alderantzizko biderkadura]] du. |
|||
=== Eremuak === |
|||
Zenbaki errealen balio absolutuaren oinarrizko lau propietateak, balio absolutuaren ideia eremu arbitrario batera orokortzeko erabil daitezke, era honetan: |
|||
<math> v</math> balio errealeko funtzio bati <math> F</math> [[Gorputz (matematika)|eremu batean]] balio absolutu deritzo (modulua, magnitudea, balioa edo balorazioa ere) lau axioma hauek betetzen baditu: |
|||
{| |
|||
|+ |
|||
|<math> v(a)\geq 0 |
|||
</math> |
|||
|<math>\text{Ez-negatibotasuna} |
|||
</math> |
|||
|- |
|||
|<math> v(a)=0 \Longleftrightarrow a=0</math> |
|||
|<math>\text{Positiboki definitua} |
|||
</math> |
|||
|- |
|||
|<math> v(ab)=v(a)v(b) |
|||
</math> |
|||
|<math>\text{Propietate biderkakorra} |
|||
</math> |
|||
|- |
|||
|<math> v(a+b)\leq v(a)+v(b)</math> |
|||
|<math>\text{Desberdintza triangeluarra} |
|||
</math> |
|||
|} |
|||
Non '''0'''-k <math> F</math>-[[Identitate gehigarria|ren identitate gehigarria]] adierazten duen. Definizio positibotik eta biderkagarritasunetik <math> v(1)=1</math> dela ondorioztatzen da , non '''1''' <math> F</math>- [[Elementu neutro|ren identitate biderkatzailea]] adierazten duen. Eremu arbitrario baterako, goian definitutako balio absolutu errealak eta konplexuak balio absolutuen adibideak dira. |
|||
<math> v</math> <math> F</math>-n balio absolutua bada, orduan <math> d(a,b)=v(a-b)</math> gisa definitutako <math> F\times F</math> -n dagoen d funtzioa, metrika bat da eta honako hauek baliokideak dira: |
|||
* <math> d</math>-k desberdintasun [[ultrametrikoa]] betetzen du <math> d(x,y)\leq max(d(x,z),d(y,z))</math> non <math> x,y,z\in F</math> |
|||
* <math> \{ v(\textstyle \sum_{k=1}^n 1 \displaystyle):n \in \N \}</math> '''R''' barruan [[Multzo mugatua|mugatuta]] dago . |
|||
# <math>\operatorname{Re}(z)\leq |z|</math> . |
|||
* <math> n \in \N</math> bakoitzarentzat <math> v(\textstyle \sum_{k=1}^n 1 \displaystyle)\leq 1</math> . |
|||
* <math> v(a)\leq 1 \Rightarrow v(1+a)\leq 1 </math> <math> a \in F</math> guztientzat . |
|||
* <math> v(a+b)\leq \max \{ v(a),v(b) \}</math> <math> a,b \in F</math> guztientzat. |
|||
Balio absolutua goiko edozein baldintza edo baldintza guztiak asetzen baditu '''ez-Arkimedianoa''' dela esaten da; bestela [[Arkimedear eremua|Arkimed]]<nowiki/>ianoa<ref>{{Erreferentzia|izena=Eric|abizena=Schechter|izenburua=Handbook of Analysis and Its Foundations|argitaletxea=Academic Press|hizkuntza=en|data=1996-10-24|url=https://books.google.es/books?id=eqUv3Bcd56EC&pg=PA260&redir_esc=y#v=onepage&q&f=false|isbn=978-0-08-053299-8|sartze-data=2021-11-03}}</ref> dela esaten da. |
|||
Gainera, {{Nowrap|<math>(w_k)_{k=1}^{n}</math>,}} zenbaki konplexuen edozein familiarentzat {{Nowrap|<math display="inline">\sum_k w_k = \sum_k \operatorname{Re} (w_k) + i \sum_k \operatorname{Im} (w_k)</math>.}} betetzen da. Zehazki, |
|||
== Balio absolutuaren programazioa == |
|||
# |
|||
[[Programazio|Programazio arloan]], balio absolutua kalkulatzeko gehien erabiltzen den [[Funtzio (matematika)|funtzio matematikoa]] <code>abs()</code> da. Funtzio hau, zenbaki osoak, errealak eta konplexuak onartzen dituzten [[FORTRAN|Fortran]], [[MATLAB|Matlab]] eta [[GNU Octave]] [[Programazio-lengoaia|programazio lengoaietan]] erabiltzen da. [[C (programazio lengoaia)|C programazio lengoaian]] ere erabiltzen da, non: |
|||
# <math display="inline">\sum_k w_k \in \R</math> bada, orduan <math display="inline">\sum_k w_k =\sum_k \operatorname{Re} (w_k)</math> . |
|||
<code>labs()</code>, <code>llabs()</code>, <code>fabs()</code> ,<code>fabsf()</code> eta <code>fabsl()</code> funtzioak ere baliozkoak diren. |
|||
( {{EkuazioOhar|⁎}} )-ren '''''froga''''' ''''':''''' aukeratu <math>c \in \C</math> zeinetarako <math>|c| = 1</math> eta <math display="inline">\left|\sum_k z_k\right| = c \left(\sum_k z_k\right)</math> (non k=1,...n ) betetzen den. Ondorengo kalkuluak bilatzen ari garen desberdintza ematen du: |
|||
: <math>\left|\sum_k z_k\right|\; \overset{(1)} {=}\; c\left(\sum_k z_k\right) = \sum_k cz_k\; \overset{(3)} {=}\;\sum_k\operatorname{Re}(cz_k)\; \overset{(2)} {\le}\; \sum_k |cz_k| = \sum_k \left|c\right| \left|z_k\right| = \sum_k \left| z_k \right| .</math> |
|||
Zenbaki osoen balio absolutu funtzioaren kodeketa hurrengoa da:<syntaxhighlight lang="c"> |
|||
Froga honengatik argi dago (⁎) berdintasuna betetzen dela, baldin eta <math>c z_k</math> zenbaki erreal ez-negatiboak badira, eta, aldi berean, zeroren ezberdinak diren <math>z_k</math> guztiek [[Argumentu (analisi konplexua)|argumentu]] bera badute. Hau da, <math>z_k = a_k\zeta</math> da, <math>\zeta</math> konstante konplexu baterko eta <math>a_k \geq 0</math> konstante erreal baterako, non {{Nowrap|<math>1 \le k \le n</math>.}}den . |
|||
int abs (int i) |
|||
{ |
|||
if (i < 0) |
|||
return -i; |
|||
else |
|||
return i; |
|||
} |
|||
</syntaxhighlight>Hala ere, [[Puntu mugikorra|koma mugikorrekin]] lan egiterako orduan, kodeaketa zailtzen da. Izan ere, [[infinitu]] eta [[NaN]] balioekin nahastu egiten da kodeketa. [[Laguntza:Erreferentziak|[erreferentzia behar]]] Mihiztadura-[[Mihiztadura-lengoaia|lengoaiarekin]] zenbaki baten balio absolutua kalkulatzea posible da hiru argibide erabiliz. Adibidez, [[X86|x86 arkitekturan]], 32 [[Bit|biteko erregistro]] baterako, hurrengo [[Intel]] sintaxia dugu:<syntaxhighlight> |
|||
cdq |
|||
xor eax, edx |
|||
sub eax, edx |
|||
</syntaxhighlight><code>cdq</code> komandoak, <code>eax</code> komandoaren zeinuaren bit-a <code>edx-en</code> hedatzen du.<code>eax</code>negatiboa ez bada, orduan <code>edx</code>zero bihurtzen da eta azken bi argibideek ez dute eraginik, <code>eax</code>aldatu gabe utziz. <code>eax</code>negatiboa bada, berriz, <code>edx</code>0xFFFFFFFF edo -1 bihurtzen da. Hurrengo bi argibideak [[Bi osagarria|bi osagarrien]] inbertsio bihurtzen dira, balio negatiboaren balio absolutua <code>eax</code>-en utziz. |
|||
== Erreferentziak == |
|||
<math>f</math> neurgarria izateak, <math>|f|</math> neurgarria dela inplikatzen duenez , ( {{EkuazioOhar|⁎⁎}} ) desberdintzaren froga, teknika bera erabiliz burutzen da, <math display="inline">\sum_k(\cdot)</math> adierazpena <math display="inline">\int_E (\cdot)\, dx</math> -rekin eta <math>z_k</math> adierapena {{Nowrap|<math>f(x)</math>.}} -rekin ordezkatuz. |
|||
<references /> |
|||
== Kanpo estekak == |
== Kanpo estekak == |
||
16:56, 3 azaroa 2021ko berrikusketa
Matematikan, zenbaki erreal baten balio absolutua edo modulua[1], gisan adierazten dena, zeinua kontuan hartu gabe -positiboa nahiz negatiboa[2] izan- zenbaki horrek duen balio ez-negatiboa da. Adibidez, -ren balio absolutua da eta -ren balio absolutua da.
Balio absolutua magnitudearen, distantziaren eta normaren ideiekin lotuta dago testuinguru matematiko eta fisiko desberdinetan. Zenbaki erreal baten balio absolutuaren kontzeptua beste matematikako objektu askotara orokor daiteke, hala nola, koaternioietara, eraztun ordenatuetara, gorputz edo espazio bektorialetara.

Terminologia eta notazioa
1806an, Jean-Robert Argand-ek modulu terminoa sartu zuen, frantsesez neurri-unitatea esan nahi duena, bereziki balio absolutu konplexurako[3][4], eta 1866an ingelesean barneratu zuten latinezko modulu baliokide gisa[3]. Balio absolutu terminoa, gutxienez, 1806tik erabili da frantsesez[5] eta 1857tik ingelesez[6]. Alde bakoitzeko barra bertikal |x| notazioa Karl Weierstrass-ek sartu zuen 1841ean[7]. Balio absoluturako beste termino batzuk zenbakizko balioa[3] eta magnitudea izan daitezke[3]. Programazio-hizkuntzetan eta software konputazionaleko paketeetan, x-ren balio absolutua abs(x) edo antzeko adierazpen baten bidez adierazten da.
Barra bertikaletako idazkera beste zenbait testuinguru matematikotan ere agertzen da: adibidez, multzo bati aplikatzean, bere kardinala adierazten du; matrize bati aplikatzen zaionean, bere determinantea adierazten du. Barra bertikalek balio absolutua adierazten dute balio absolutua definituta dagoen objektu aljebraikoetarako soilik, bereziki zatiketa normatu aljebraikoaren elementu baterako, adibidez, zenbaki erreal baterako, zenbaki konplexu baterako edo kuaternioi baterako. Barra bertikalen erabilera -ko bektore baten norma euklidear [8]eta goi normarako[9], oso erlazionatuta dagoen baina desberdina den notazioa da, nahiz eta azpiindizedun barra bertikal bikoitzak ( eta , hurrenez hurren) notazio arruntagoak eta ez hain anbiguoak diren.
Definizioa
Zenbaki errealak
Edozein zenbaki errealen balio absolutua edo modulua, honela adierazten da: eta modu honetan definitzen da:[10]
-ren balio absolutua beti da zenbaki positiboa edo zero, baina inoiz ez negatiboa: zenbaki negatiboa denean , haren balio absolutua nahitaez positiboa da .
Ikuspuntu geometrikotik, zenbaki erreal baten balio absolutua zenbaki horren eta zeroaren artean dagoen distantzia bezala ikus daiteke. Oro har, bi zenbakiren arteko aldearen balio absolutua haien arteko distantzia da.
Propietateak
Balio absolutuak funtsezko lau propietate hauek ditu, izanik:
Beste propietate erabilgarri batzuk ondoko hauek dira:
horiek definizioaren edo lehenengo lau propietateen ondoriok dira.
Desberdintasunak erabiltzen dituzten beste bi propietate, ondokoak dira:
Erlazio horiek balio absolutua duten desberdintasunak ebazteko erabil daitezke, adibidez:
Zenbaki konplexuak
Zenbaki konplexuak ez daudenez ordenatuta, zenbaki errealentzat emandako balio absolutuaren definizioa ezin zaie zuzenean aplikatu. Hala ere, zenbaki erreal baten balio absolutuaren interpretazio geometrikoa 0tik bere distantziara orokor daiteke. Eta beraz, zenbaki konplexu baten balio absolutua plano konplexuan dagokion puntutik jatorriraino dagoen distantzia euklidearrak definitzen du. Hau Pitagorasen teorema erabiliz kalkula daiteke: edozein zenbaki konplexutarako.

non eta zenbaki errealak diren, -ren balio absolutua edo modulua ikurraren bidez adierazten da eta honela definitzen da[11]:
,
non eta -ren zati erreala eta irudikaria diren, hurrenez hurren. zati irudikaria 0 denean, hau bat dator zenbaki errealaren balio absolutuaren definizioarekin.
zenbaki konplexua bere forma polarrean honela adierazten da:
,
non (eta -ren argumentua (edo fasea)), bere balio absolutua honakoa da:
.
Edozein zenbaki konplexuren eta balio absolutu bera duen bere konjugatu konplexuaren arteko produktua, () zenbaki erreal ez-negatiboa da beti. Gainera, zenbaki konplexu baten balio absolutua produktuaren erro karratua da, horregatik, karratu absolutua edo karratu modulua deritzo:
.
Honek zenbaki errealentzako definizio alternatiboa orokortzen du:
Zenbaki konplexuentzako balio absolutuak, goian zenbaki errealen balio absolutuarentzat emandako oinarrizko lau propietateak partekatzen ditu.
Talde-teoriaren hizkuntzan, biderkatze propietatea hurrengo moduan berridatz daiteke: balio absolutua da zenbaki konplexuen biderkatze-taldetik zenbaki erreal positiboen biderkatze-taldera doan homomorfismo-talde bat[12].
Azpigehigarritasunaren propietatea ("desberdintza triangeluar konplexua") zenbaki konplexu dituen edozein bilduma finitura honela hedatzen da:
(*)
Desberdintasun hau familia infinituetan ere aplikatzen da, baldin eta serie infinitua erabat konbergentea bada. Lebesgueren integrazioa batuketaren analogia jarraitutzat hartzen bada, funtzio neurgarriak azpimultzo batean integratuta daudenean, desberdintasun hau balio konplexuaren bidez analogikoki betetzen da. Ideia hau honela adieraz daiteke:
(**)
(Honek Riemann-en funtzio integragarriak tarte mugatu baten barnean sartzen ditu, kasu berezi gisa).
Desberdintza triangeluar konplexuaren froga
Desberdintza triangeluarra, (*) -k emanda, zenbaki konplexuen hiru propietate aplikatuta froga daiteke. Hots, zenbaki konplexu bakoitzerako:
- Existitzen da zeinetarako eta ;
Gainera, , zenbaki konplexuen edozein familiarentzat betetzen da. Zehazki,
3. bada, orduan .
(*)-ren froga: aukeratu zeinetarako |c|=1 eta betetzen diren. Ondorengo kalkuluak bilatzen ari garen desberdintza ematen digu:
Froga honi esker, argi dago (*) berdintasuna betetzen dela, baldin eta zenbaki erreal ez-negatiboak badira, eta, aldi berean, zeroren ezberdinak diren guztiek argumentu bera badute. Hau da, da, konstante konplexu baterako eta konstante erreal baterako, non . den.
neurgarria izateak neurgarria izatea inplikatzen duenez, (**) desberdintzaren froga teknika bera erabiliz burutzen da, adierazpena -rekin eta adierazpena -rekin ordezkatuz[13].
Definizio baliokidea
zenbaki erreala bada, haren balio absolutua zenbaki erreal ez-negatibo bat da, honela definitua dagoena:
- , [14] hauen arteko maximoaren berdina da.
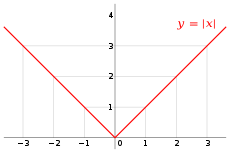
Balio absolutuaren funtzioa

Zenbaki errealen balio absolutu funtzioa zenbaki erreal guztien multzoaren gainean definitzen da, zenbaki erreal bakoitzari bere balio absolutua emanez.
Formalki, zenbaki erreal guztien balio absolutua honela definitzen da:[15]
eta honela adierazten da:
Definizioz, -ren balio absolutua beti zero edo zero baino handiagoa izango da, eta inoiz ez negatiboa.
- Balio absolutu funtzioa funtzio jarraitu bat da zuzen erreal osoan; bere deribatuak etena du (0;0) puntuan, balio konstanteko bi adar baitaude. Hau da, funtzio hori diferentziagarria da R osoan, x=0 puntuan izan ezik.
- funtzioa, balio absolutua erabiliz, funtzio gorakorra eta jarraitua da; bere grafikoa parabolaren grafikotik lortzen da , ezkerreko adarra ardatzarekiko islatuz.
Errealen multzoa balio absolutuak definitutako arauarekin, Banach espazio bat da.
Zeinu-funtzioarekiko erlazioa
Zenbaki errealen balio absolutu funtzioak bere balioa itzultzen du zeinua kontuan hartu gabe; zeinu funtzioak, berriz, zenbaki baten zeinua itzultzen du, haren balioa kontuan hartu gabe. Ekuazio hauek bi funtzio horien arteko erlazioa erakusten dute:
, den kasurako
edo
eta kasuan,
Deribatua
Balio absolutu funtzioak deribatu bat du bakoitzerako, baina ez da diferentziagarria kasuan. kasuan, aldiz, deribatua honako funtzio honek ematen du[16][17]:

Antideribatua
Zenbaki errealen balio absolutu funtzioaren integral mugagabea hurrengoa da:
non integrazio arbitrario konstantea den.
Distantzia
Balio absolutuak lotura estua du distantziaren ideiarekin. Lehen esan bezala, zenbaki erreal edo konplexu baten balio absolutua, zenbaki horrek jatorrira duen distantzia da; zenbaki errealetarako, zenbaki errealen zuzenean zehar, eta zenbaki konplexuetarako, plano konplexuan. Eskuarki, bi zenbaki errealen edo konplexuen arteko diferentziaren balio absolutua, bi zenbaki errealen edo konplexuen arteko distantzia da.
Bi eta punturen arteko distantzia euklidear estandarra n -espazio euklidearrean honela definitzen da:
Hau orokortze gisa ikus daiteke, izan ere eta errealentzat , hau da, dimentsio baten, balio absolutuaren definizio alternatiboaren arabera, honako adierazpena dugu:
eta eta zenbaki konplexuentzat , hau da, bi dimentsiotan, honako hau:
Aurrekoak erakusten du "balio absolutu"-distantzia, bat datorrela distantzia euklidear estandarrarekin, zenbaki errealentzat eta konplexuentzat. Zeintzuk oinordetzan hartzen dituzten, dimentsio bakarreko eta bi dimentsioko espazio euklidear gisa hartzearen ondorioz, hurrenez hurren.
Bi zenbaki erreal edo konplexuren diferentziaren balio absolutuaren propietateek: ez-negatibotasunak, bereizezinen identitateak, simetriak eta goian adierazitako desberdintza triangeluarrak, distantzia-funtzioaren ideia orokorragoa bultzatzen dutela ikus daiteke:
X × X multzoko d funtzio erreal bati X-ko metrika (edo distantzia funtzioa ) deitzen zaio lau axioma hauek betetzen baditu:
Orokortzeak
Zenbaki hiperkonplexuak
Zenbaki konplexuetan ez ezik, balio absolutuaren funtzioa zenbaki hiperkonplexuetara ere orokor daiteke, hala nola, kuaternioietara edo oktonioietara. Zenbaki errealen gaineko aljebran, h zenbaki baten balio absolutua honela definitzen da:
Non -ren hiperkonjugazioa den.
Eraztun ordenatuak
Goian aipatutako zenbaki errealetarako emandako balio absolutuaren definizioa edozein eraztun ordenatutara heda daiteke. Hau da, a eraztun ordenatuaren elementu bat baldin bada, a-ren balio absolutua, |a| bidez adierazten dena, honela definitzen da[18]:
non −a, a-ren alderantzizko gehigarria den, 0 identitate gehigarria den, eta < eta ≥ ikurrek eraztuneko ordenamenduari dagokion ohiko esanahia duten.
Espazio bektorialak
Artikulu nagusia: Norma (matematika)
Zenbaki errealen balio absolutuaren oinarrizko propietateak, espazio bektorial arbitrario batera orokortzeko erabil daitezke, aldaketa txiki bat eginez.
F eremu baten gaineko V espazio bektorial batean, balio errealeko funtzioari balio absolutua deritzo, || · || gisa adierazten dena. Baina, honako axioma hauek betetzen baditu, norma deitzen zaio:
F-ko a guztietarako eta V-ko u,v guztietarako,
Bektore baten norma, magnitude edo luzera izenarekin ere ezaguna da.
espazio euklidearraren kasuan, honela definitutako funtzioari
norma euklidearra deritzo. zenbaki errealak dimentsio bakarreko espazio bektorialtzat hartzen direnean, balio absolutua p-norma da, (ikusi Lp espazioa) edozein p-rentzat. Izan ere, balio absolutua norma "bakarra" da, zentzu honetan, -eko norma guztietarako, betetzen da.
Balio absolutu konplexua, barne produktu-espazio bateko normaren kasu berezi bat da. Balio absolutu hau, norma euklidearraren berdina da plano konplexua -ko plano euklidear gisa identifikatzen denean.
Konposaketa aljebraikoak
A konposaketa aljebraiko orok bere konjugazio izena hartzen duen x → x* inboluzioa du. A-n, x elementu baten eta x* elementu horren konjokatuaren arteko produktuari, x elementuaren norma deritzo eta era honetan adierazten da: N(x) = x x*.
zenbaki errealak, zenbaki konplexuak eta kuaternioiak forma koadratiko zehatzek emandako normak dituzten konposaketa aljebraikoak dira. Zatiketa-aljebra horietan, balio absolutua, aljebraren normaren konposizioaren erro karratuak ematen du.
Orokorrean, konposaketa aljebraikoaren norma definitu gabeko forma koadratikoa izan daiteke eta bektore nuluak ditu. Hala ere, zatiketa-aljebren kasuan bezala, x elementu batek zero ez den norma duenean, orduan x-k x*/N (x) -k emandako alderantzizko biderkadura du.
Eremuak
Zenbaki errealen balio absolutuaren oinarrizko lau propietateak, balio absolutuaren ideia eremu arbitrario batera orokortzeko erabil daitezke, era honetan:
balio errealeko funtzio bati eremu batean balio absolutu deritzo (modulua, magnitudea, balioa edo balorazioa ere) lau axioma hauek betetzen baditu:
Non 0-k -ren identitate gehigarria adierazten duen. Definizio positibotik eta biderkagarritasunetik dela ondorioztatzen da , non 1 - ren identitate biderkatzailea adierazten duen. Eremu arbitrario baterako, goian definitutako balio absolutu errealak eta konplexuak balio absolutuen adibideak dira.
-n balio absolutua bada, orduan gisa definitutako -n dagoen d funtzioa, metrika bat da eta honako hauek baliokideak dira:
- -k desberdintasun ultrametrikoa betetzen du non
- R barruan mugatuta dago .
- bakoitzarentzat .
- guztientzat .
- guztientzat.
Balio absolutua goiko edozein baldintza edo baldintza guztiak asetzen baditu ez-Arkimedianoa dela esaten da; bestela Arkimedianoa[19] dela esaten da.
Balio absolutuaren programazioa
Programazio arloan, balio absolutua kalkulatzeko gehien erabiltzen den funtzio matematikoa abs() da. Funtzio hau, zenbaki osoak, errealak eta konplexuak onartzen dituzten Fortran, Matlab eta GNU Octave programazio lengoaietan erabiltzen da. C programazio lengoaian ere erabiltzen da, non:
labs(), llabs(), fabs() ,fabsf() eta fabsl() funtzioak ere baliozkoak diren.
Zenbaki osoen balio absolutu funtzioaren kodeketa hurrengoa da:
int abs (int i)
{
if (i < 0)
return -i;
else
return i;
}
Hala ere, koma mugikorrekin lan egiterako orduan, kodeaketa zailtzen da. Izan ere, infinitu eta NaN balioekin nahastu egiten da kodeketa. [erreferentzia behar] Mihiztadura-lengoaiarekin zenbaki baten balio absolutua kalkulatzea posible da hiru argibide erabiliz. Adibidez, x86 arkitekturan, 32 biteko erregistro baterako, hurrengo Intel sintaxia dugu:
cdq
xor eax, edx
sub eax, edxcdq komandoak, eax komandoaren zeinuaren bit-a edx-en hedatzen du.eaxnegatiboa ez bada, orduan edxzero bihurtzen da eta azken bi argibideek ez dute eraginik, eaxaldatu gabe utziz. eaxnegatiboa bada, berriz, edx0xFFFFFFFF edo -1 bihurtzen da. Hurrengo bi argibideak bi osagarrien inbertsio bihurtzen dira, balio negatiboaren balio absolutua eax-en utziz.
Erreferentziak
- ↑ Jean-Robert Argand, introductor del término módulo en 1806, ver: Nahin, O'Connor and Robertson, 5- y +5 igual a Cinco yfunctions.Wolfram.com.
- ↑ Txantiloi:Cita libro
- ↑ a b c d Oxford English Dictionary, Draft Revision, June 2008
- ↑ Nahin, O'Connor and Robertson, and functions.Wolfram.com.; for the French sense, see Littré, 1877
- ↑ Lazare Nicolas Marguerite Carnot. 2020-12-30 (Noiz kontsultatua: 2021-11-03).
- ↑ (Ingelesez) James Mills Peirce. (1857). A Text-book of Analytic Geometry: On the Basis of Professor Peirce's Treatise. J. Bartlett (Noiz kontsultatua: 2021-11-03).
- ↑ Higham, Nicholas J.. (2020). Handbook of writing for the mathematical sciences. (Third edition. argitaraldia) ISBN 978-1-61197-609-0. PMC 1131865104. (Noiz kontsultatua: 2021-11-03).
- ↑ Spivak, Michael. (1965). Calculus on manifolds : a modern approach to classical theorems of advanced calculus. ISBN 0-8053-9021-9. PMC 187146. (Noiz kontsultatua: 2021-11-03).
- ↑ Munkres, James R.. (1991). Analysis on manifolds. Addison-Wesley Pub. Co., Advanced Book Program ISBN 978-1-4294-8504-3. PMC 170966279. (Noiz kontsultatua: 2021-11-03).
- ↑ Dolciani y otros. álgebra moderna
- ↑ González, Mario O.. (1992). Classical complex analysis. M. Dekker ISBN 0-585-31691-0. PMC 45728566. (Noiz kontsultatua: 2021-11-03).
- ↑ Lorenz, Falko. (2006-2008). Algebra. Springer ISBN 978-0-387-31608-6. PMC 209914197. (Noiz kontsultatua: 2021-11-03).
- ↑ Rudin, Walter. (1976). Principles of mathematical analysis. (Third edition. argitaraldia) ISBN 0-07-054235-X. PMC 1502474. (Noiz kontsultatua: 2021-11-03).
- ↑ Spivak. Calculus I
- ↑ functions.Wolfram.com introducción de la notación , por Karl Weierstrass en 1841.
- ↑ (Ingelesez) Weisstein, Eric W.. «Absolute Value» mathworld.wolfram.com (Noiz kontsultatua: 2021-11-03).
- ↑ Bartle, Robert G.. (1982). Introduction to real analysis. Wiley ISBN 0-471-05944-7. PMC 7875643. (Noiz kontsultatua: 2021-11-03).
- ↑ (Ingelesez) Lane, Saunders Mac; Birkhoff, Garrett. (1999). Algebra. American Mathematical Soc. ISBN 978-0-8218-1646-2. (Noiz kontsultatua: 2021-11-03).
- ↑ (Ingelesez) Schechter, Eric. (1996-10-24). Handbook of Analysis and Its Foundations. Academic Press ISBN 978-0-08-053299-8. (Noiz kontsultatua: 2021-11-03).









































![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


































































































