Lankide:Santi Dzrg/Funtzio jarraitu

Matematikan, funtzio jarraitua dela esaten da aldagai askean izandako aldaketa txikiek funtzioaren balioan ere aldaketa txikiak eragiten dituztenean. Jarraituak ez diren funtzioak ez-jarraituak dira. Alderantzizko jarraitua duen funtzio jarraituari homeomorfismo deritzo.

Funtzioen jarraitutasuna topologiaren oinarrizko kontzeptua da, ------. Artikulu honen sarrera aldagai errealetako funtzioetan ardazten da. Jarraitutasunaren beste kasu sendoago bat jarraitutasun uniformea da. Gainera, artikulu honetan bi espazio metrikoren arteko funtzioen jarraitutasunaren definizio orokorragoa lantzen da. Ordena teorian, batez ere domeinu teorian, Scotten jarraitutasuna kontsideratu daiteke. Beste jarraitutasun motak existitzen dira, baina ez dira lantzen artikulu honetan.

Adibidez, izan bedi h(t) funtzio, lore baten altuera deskribatzen duenta t denboran. Funtzio hau jarraitua da. Aldiz, M(t) banku kontu batean dagoen diru kopurua adierazten badu t denboran, funtzioak salto egiten du dirua sartu edo ateratzen denean; beraz funtzio ez-jarraitua da.

Historia

Jarraitutasunaren epsilon-delta erako lehen definizioa Bernard Bolzanok eman zuen 1817. urtean. Cauchyk horrela definitu zuen $y=f(x)$-ren jarraitutasuna:

«	$\alpha$ aldaketa infinituki txikia x aldagai askean beti eragiten du $f(x+\alpha )-f(x)$ aldaketa infinituki txikia y aldagai dependentean.	»
Augustin-Louis Cauchy: Cours d'Analyse, 1821, 34. orrialdea

Cauchyk kantitate infinituki txikiak kantitate aldakorren arabera definitu zituen, eta bere definizioa gaur egungo definizio infinitesimalaren antzekoa da (ikus mikrojarraitutasuna). Puntuz puntuko jarraitutasunaren eta jarraitutasun uniformearen arteko desberdintasuna eta definizioa Bolzanok eman zituen 1830ko hamarkadan, baina bere lana ez zen 1930ko hamarkada arte argitaratu. Bolzano bezala, Karl Weierstrassek funtzio baten jarraitutasuna c puntuan ukatzen zuen funtzioa c-n eta bere bi aldeetan definituta baldin ez bazegoen, baina Édouard Goursatek funtzioa c-ren alde bakarrean definituta egotea baimendu zuen eta Camille Jordanek baimendu zuen c-n bakarrik definituta bazegoen ere. Puntuz puntuko jarraitutasunaren hiru definizio ez-baliokide hauek oraindik erabiltzen dira. Edouard Heinek eman zuen jarraitutasun uniformearen lehen definizio argitaratua 1872. urtean, baina bere ideiak Dirichletek eman zituen 1854. urtean.

Real functions

Definizioa

$f(x)={\tfrac {1}{x}}$ funtzioa $\mathbb {R} \smallsetminus \{0\}$ definizio-eremuan jarraitua da, baina ez da jarraitua $R$ osoan, $x=0$ puntuan ez dagoelako definituta.</math>

Funtzio erreal bat, hau da, zenbaki errealetatik zenbaki errealetara doan funtzio bat; grafo baten bitartez irudikatu daiteke plano kartesiarrean. Funtzio hori jarraitua da grafoa kurba ez-apurtu baten bitartez irudikatu baldin badaiteke, kurbaren definizio-eremua zuzen erreal osoa izanda. Jarraian definizio zehatzago bat ematen da.

Funtzio errealen jarraitutasunaren definizio zehatza limiteen bitartez ematen ohi da. $f$ funtzio bat $x$ aldagaiarekin $c$ puntuan jarraitua da baldin eta $f(x)$-ren limitea $x$ $c$ hurbiltzen den bitartean $f(c)$-ren berdina bada. Gainera, funtzioa jarraitua da puntu guztietan jarraitua bada. Funtzio bat ez-jarraitua da punturen batean ez jarraitua denean.

Funtzio baten jarraitutasunaren hainbat definizio existitzen dira. Batzuetan esaten da funtzio bat jarraitua dela jarraitua bada bere definizio-eremuko puntu guztietan. Adibidez, $f(x)=tan(x)$ funtzioa jarraitua bere definizio eremuan (zenbaki errealak non $x\neq (2n+1)\pi /2$, $n$ edozein zenbaki oso izanda). Batzuetan, salbuespenak egiten dira definizio-eremuaren mugekin. Adibidez, $f(x)={\sqrt {(}}x)$ funtzioaren grafoa, bere domeinua zenbaki erreal ez-negatiboak izanda; ezkerraldean amaiera puntua dauka. Kasu honetan eskuinaldeko limitea bakarrik behar da funtzioaren balioa lortzeko. Definizio honen arabera, $f$ jarraitua da $x=0$ mugan eta zenbaki ez-negatibo guztietan. Definiziorik arruntenaren arabera, funtzio bat jarraitua da zenbaki erreal osoetan jarraitua bada. Kasu honetan, aurreko bi adibideak ez dira jarraituak, baina edozein polinomioren funtzioa jarraitua da, sinua, kosinua eta esponentziala bezala. Beraz, jarraitu hitzaren erabilpen arduratsua egin behar da, testuinguruaren arabera bere esanahia aldatu daitekelako.

Notazio matematikoa erabilita, aurreko hiru zentzuetan jarraitutasuna definitzeko hainbat era daude.

Izan bedi

$f\colon D\rightarrow \mathbf {R} \quad$ zenbaki errealen $D$ azpimultzoan definitutako funtzioa.

$D$ azpimultzoa $f$-ren definizio-eremua da. Aukera posibleen artean ondorengoak daude:

$D=\mathbf {R} \quad$ (zenbaki errealen multzo osoa), edo, $a$ eta $b$ zenbaki errealentzat,

$D=[a,b]=\{x\in \mathbf {R} \,|\,a\leq x\leq b\}\quad$ ($D$ tarte itxia da), edo

$D=(a,b)=\{x\in \mathbf {R} \,|\,a<x<b\}\quad$ ($D$ tarte irekia da).

$D$ tarte irekia bada, $a$ eta $b$ ez dira mugak aurreko zentzuan bezala, eta beraz $f(a)$ eta $f(b)$-ren balioek ez dute ondoriorik $D$-ko jarraitutasunean.

Funtzioen limiteen bidezko definizioa

$f$ funtzioa bere definizio-eremuko $c$ puntuan jarraitua da $f(x)$-ren limitea $x$ $c$-ra hurbiltzen den heinean ($f$-ren definizio-eremuan zehar) existitzen bada eta $f(c)$-ren berdina bada. Notazio matematikoan, hurrengoaren baliokidea da:

$\lim _{x\to c}{f(x)}=f(c).$

Benetan, honek hiru baldintza inplikatzen ditu: lehenik, $f$ $c$ puntuan definituta dago (betetzen dena, $c$ $f$-ren definizio-eremuan dagoelako). Bigarren, limitea existitu behar da. Hirugarren, limitearen balioa $f(c)$-ren berdina izan behar da.

(Asumitu dugu $f$-ren definizio eremuak ez duela puntu isolaturik. Adibidez, tarteek edo tarteen bildurek ez dute puntu isolaturik.)

Inguruneen bidezko definizioa

$c$ puntuaren ingurunea $c$-tik distantzia finko bat baino hurbilago dauden definizio-eremuko puntu guztiak dituen multzo bat da. Intuitiboki, funtzio bat jarraitua da $c$ puntuan $f$-ren murrizketa $c$-ren ingurune batean $f(c)$ puntu bakarrera txikitzen bada $c$-ren inguruko ingurunearen zabalera zerorantz doanean. Zehazki, $f$ funtzioa jarraitua da bere definizio-eremuko $c$ puntuan, baldin edozein ingurunerentzat $N_{1}(f(c))$ existitzen bada ingurune bat $N_{2}(c)$ non $f(x)\in N_{1}(f(c))$, $x\in N_{2}(c)$ denean.

Definizio honek bakarrik behar du eremua eta koeremua espazio topologikoak izatea, eta ondorioz definiziorik orokorrena da. Ondoriozta daiteke definizio honetatik $f$ funtzioa jarraitua dela bere definizio-eremuko puntu isolatu guztietan. Adibidez, balio errealdun funtzio guztiak jarraituak dira zenbaki osoen multzoan.

Segiden limiteen bidezko definizioa

$e^{1/n}$ segidak $e^{0}$-rantz doa.

Ordez, eskatu daiteke $c$-rantz konbergenteak diren definizio-eremuko puntuez osatutako segida guztientzat ($(x_{n})_{n\in \mathbb {N} }$) $\left(f(x_{n})\right)_{n\in \mathbb {N} }$ segida $f(c)$-rantz konbergentea izatea. Notazio matematikoan:

$\forall (x_{n})_{n\in \mathbb {N} }\subset D:\lim _{n\to \infty }x_{n}=c\Rightarrow \lim _{n\to \infty }f(x_{n})=f(c)\,$

Weierstrassen eta Jordanen definizioa

ε-δ-definizioaren irudikapena: ε=0.5-rentzat, c=2, δ=0.5 balioak definizioaren baldintza betetzen du.

Funtzio baten limitearen definizioa sartzean, hurrengo definizioa lortzen da: $f$ funtzio bat emanda, bere definizio eremuko $x_{0}$ puntuan jarraitua da baldin edozein $\varepsilon$ positiborentzat existitzen bada $\delta$ positibo bat non $x_{0}-\delta <x<x+\delta$ betetzen duten $x$-entzat:

$f(x_{0})-\varepsilon <f(x)<f(x_{0})+\varepsilon .$

Beste era batean idatzita, $f$ jarraitua bada definizio-eremuko $x_{0}$ puntuan, edozein $\varepsilon$ positiborentzat existitzen da $\delta$ positiboa non definizio eremuko $x$ guztientzat:

$|x-x_{0}|<\delta \Rightarrow |f(x)-f(x_{0})|<\varepsilon .$

Era intuitiboago batean, esan daiteke behar badela $f(x)$-ren balioak $f(x)$-ren ingurune batean egotea, behar den gauza bakarra $x_{0}$-ren ingurune egoki bat aukeratzea da $x$-k balioak hartzeko. Nahi dugun beste txikitu ahal bada $f(x)$-ren ingurunea, orduan $f$ jarraitua da $x_{0}$-ren inguruan.

Gaur egungo hizkera matematikoan, honako hau orokortzen da oinarri batekiko funtzio baten jarraitutasunaren definizioaren bitartez, kasu honetan topologia metrikoa.

Weierstrassek behartu zuen $x_{0}-\delta <x<x+\delta$ tartea definizio eremuan egotera, baina Jordanek baldintza hori kendu zuen.

Ondarraren kontrolaren bidezko definizioa

Analisi numerikoan eta frogak egiteko, askotan beharrezkoa da jakitea zein azkarrak diren limiteen konbergentziak, hau da; ondarraren kontrola. Hori formalizatu daiteke jarraitutasunaren definizio bat sortzeko.

Funtzio bat $C:[0,\infty )\to [0,\infty ]$ kontrol-funtzioa da baldin

• $C$ ez beherakorra bada.
• $\inf _{\delta >0}C(\delta )=0$

$f$ funtzio erreala jarraitua da $x_{0}$-n baldin

$|f(x)-f(x_{0})|\leq C(|x-x_{0}|)$, definizio eremuan dauden $x$ guztietarako

Funtzio bat jarraitua da $x_{0}$-n $C$-jarraitua baldin bada $C$ kontrol-funtzio batentzako.

Estrategia hau erabiliz jarraitutasunaren kontzeptua findu daiteke erabili daitezkeen kontrol-funtzioak murriztuz. ${\mathcal {C}}$ kontrol-funtzioen multzoa izanda, funtzio bat ${\mathcal {C}}$-jarraitua da baldin $C$-jarraitua bada $C\in {\mathcal {C}}$ batentzako. Adibidez, $\alpha$ esponentedun Lipschitzen eta Hölderren jarraitutasunak hurrengo multzoekin definitzen dira:

${\mathcal {C}}_{\mathrm {Lipschitz} }=\{C|C(\delta )=K|\delta |,\ K>0\}$

${\mathcal {C}}_{{\text{Hölder}}-\alpha }=$$\{C|C(\delta )=K|\delta |^{\alpha },\ K>0\}$.

Oszilazioen bidezko definizioa

Funtzio bat puntu batean jarraitua ez izatea bere oszilazioaren bidez kuantifikatu daiteke.

Jarraitutasuna oszilazioen bidez definitu daiteke ere: $f$ funtzioa jarraitua da $x$ puntuan baldin eta soilik baldin bere oszilazioa puntu horretan zero bada, notazio matematikoan $\omega _{f}(x_{0})=0$. Notazio honen abantaila bat ez-jarraitutasuna kuantifikatzen duela da: oszilazioak esaten du zenbatekoa den ez-jarraitutasuna puntu batean.

Definizio hau erabilgarria da multzo teoria deskribakorrean puntu ez-jarraituen multzoak eta puntu jarraituak (oszilazioa $\varepsilon$ baino txikiagoa duten multzoen ebakidura (G_δ multzo bat)) ikertzeko. Gainera, definizio honek Lebesgueren integragarritasun baldintzaren norabide bateko froga azkarra ematen du.

Oszilazioa ε-δ definizioaren berrantolapen baten baliokidea da, limiteak erabiliz oszilazioa definitzeko: puntu batean $\varepsilon _{0}>0$ batentzat ez bada existitzen $\delta$-rik non baldintza betetzen den, orduan oszilazioa gutxienez $\varepsilon _{0}$ da. Aldiz, $\varepsilon$ guztientzat $\delta$ existitzen bada, oszilazioa 0 da. Oszilazioen bidezko definizioa espazio topologikoetatik espazio metrikoetara doazen funtzioetara orokortu daiteke.

Hipererrealen bidezko definizioa

Cauchyk emandako jarraitutasunaren definizioa ideia intuitiboetan oinarritzen da: aldagaian egindako aldaketa infinitesimal batek funtzioaren balioan aldaketa infinitesimala eragiten du. Kalkulu ez-estandarraren bidez definizio hori matematikoki zehatza egin daiteke. Zuzen erreala zenbaki infinitu eta infinitesimalen bidez handitu daiteke zenbaki hipererrealak sortzeko. Kalkulu ez-estandarrean jarraitutasuna horrela definitu daiteke, Cauchyren definizioa gaur egungo notaziora "itzuliz":

$f$ funtzio erreala jarraitua da $x$ puntuan baldin bere hipererrealetako hedadura hurrengo propietatea betetzen badu: $dx$ infinitesimal edozeinerako, $f(x+dx)-f(x)$ infinitesimala da.

Funtzio jarraituen eraikuntza

Funtzio kubiko baten grafoa leuna da. Funtzioa jarraitua da.

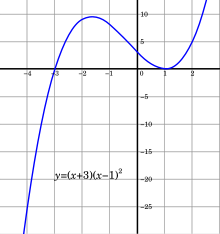
Funtzio baten jarraitutasuna ebaluatzeko prozesua sinplifikatu daiteke aurreko propietateak ebaluatuz funtzioaren "blokeetan". Erreza da frogatzea definizio-eremu batean jarraituak diren bi funtzioen batuketa jarraitua dela eremu horretan. Bi funtzio emanda

$f,g\colon D\rightarrow \mathbf {R}$,

orduan funtzio jarraituen batura

$s=f+g$

($s(x)=f(x)+g(x)$ izanda, $x\in D$ guztientzat) jarraitua da $D$-n.

Gauza bera gertatzen da funtzio jarraituen biderketarekin

$p=f\cdot g$

($p(x)=f(x)\cdot g(x)$ izanda, $x\in D$ guztientzat) jarraitua da $D$-n.

Aurreko emaitzak funtzio konstanteen eta identitate funtzioaren ($I(x)=x$) jarraitutasunarekin konbinatuz, funtzio polinomikoen jarraitutasuna zenbaki errealetan ondoriozta daiteke. Adibidez

$f(x)=x^{3}+x^{2}-5x+3$

(eskuineko irudian irudikatua).

Funtzio arrazional baten grafoa. Funtzioa ez dago definituta $x=-2$ puntuan. Marra horizontala eta bertikala asintotak dira.

Era berean froga daiteke funtzio baten alderantzizkoa (biderkadurarekiko)

$r=1/f$

($r(x)=1/f(x)$ izanda $x\in D$ guztientzat non $f(x)\neq 0$) jarraitua dela $D\smallsetminus \{x:f(x)=0\}$-n.

Horrek inplikatzen du funtzio jarraituen zatiketa ($g$-ren erroak kenduta)

$q=f/g$

($q(x)=f(x)/g(x)$ izanda $x\in D$ guztientzat non $g(x)\neq 0$) ere jarraitua dela $D\smallsetminus \{x:g(x)=0\}$-n.

Adibidez, hurrengo funtzioa (eskuineko irudian)

$y(x)={\frac {2x-1}{x+2}}$

definituta dago zenbaki erreal guztientzat ($x=2$ izan ezik), eta jarraitua da puntu horietan. Beraz, funtzio jarraitua da. $x=2$ puntuan ez da jarraitua, puntu hori ez dagoelako funtzioaren definizio-eremuan. Ez da existitzen $F\colon \mathbf {R} \rightarrow \mathbf {R}$ funtzio jarraiturik $y(x)$-rekin bat datorrenik $x\neq 2$ guztientzat.

sinc eta cos funtzioak.

Sinu funtzioa zenbaki erreal osoetan jarraitua denez, sinc funtzioa ($G(x)=sin(x)/x$) definituta dago eta jarraitua da $x\neq 0$ erreal guztientzat. Kasu honetan, hala era, $G$ zenbaki erreal guztietan jarraitua den funtzio batera luzatu daiteke; $G(0)=1$ ezartzen. Izan ere, hori da funtzioaren limitea 0-rantz hurbiltzen denean:

$G(0)=\lim _{x\rightarrow 0}{\frac {\sin x}{x}}=1.$

Beraz, ezarriz

$G(x)={\begin{cases}{\frac {\sin(x)}{x}}&{\text{ if }}x\neq 0\\1&{\text{ if }}x=0,\end{cases}}$

sinc funtzioa zenbaki erreal osoetan jarraitua den funtzio batean bihurtzen da. Puntu singular saihesgarri izena erabiltzen da kasu hauetan, non funtzioaren balioak definitu daitezke funtzioa jarraitua egiteko puntu zehatzetan.

Funtzioen arteko beste eragiketa bat funtzioen konposaketa da. Bi funtzio jarraitu izanda

$\quad g\colon D_{g}\subseteq \mathbf {R} \rightarrow R_{g}\subseteq \mathbf {R} \quad {\text{and}}\quad f\colon D_{f}\subseteq \mathbf {R} \rightarrow R_{f}\subseteq D_{g},$

beraien konposizioa ($c=g\circ f\colon D_{f}\rightarrow \mathbf {R}$), $c(x)=g(f(x))$ izanda, jarraitua da.

Aurreko proposizioa erabiltzen lortzen da, adibidez

$e^{\sin(\ln x)}$ jarraitua dela $x>0$ guztietarako.

Funtzio ez-jarraituen zenbait adibide

Zeinu funtzioaren irudikapena. $\lim _{n\to \infty }\operatorname {sgn} \left({\tfrac {1}{n}}\right)\neq \operatorname {sgn} \left(\lim _{n\to \infty }{\tfrac {1}{n}}\right)$ dela ikus daiteke. Beraz, zeinu funtzioa ez-jarraitua da 0 puntuan.

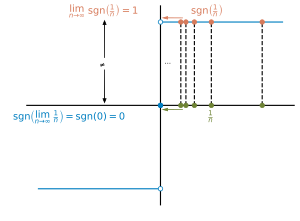
Funtzio ez-jarraituen adibide bat Heavisideren eskailera funtzioa da ($H$), horrela definituta:

$H(x)={\begin{cases}1&x\geq 0{\text{ bada }}\\0&x<0{\text{ bada }}\end{cases}}$

Hartu adibidez $\varepsilon =1/2$. Ez dago $x=0$-ren inguruko $\delta$-ingurunerik (hau da, $(-\delta ,\;\delta )$ tarte irekia, $\delta >0$ izanda) non $H(x)$-ren balioak $H(0)$-ren $\varepsilon$-ingurunean egongo diren (hau da, $(1/2,\;3/2)$-n). Intuitiboki, ez-jarraitutasun mota hau funtzioaren balioetan gertatzen den bat-bateko jauzia da.

Antzeko kasu bat zeinu funtzioarena da:

$\operatorname {sgn}(x)={\begin{cases}\;\;\ 1&x>0{\text{ bada }}\\\;\;\ 0&x=0{\text{ bada }}\\-1&x<0{\text{ bada }}\end{cases}}$

ez-jarraitua da $x=0$ puntuan, baina jarraitua da beste puntu guztietan. Hurrengo adibide honetan:

$f(x)={\begin{cases}\sin \left(x^{-2}\right)&x\neq 0{\text{ bada }}\\0&x=0{\text{ bada }}\end{cases}}$

funtzioa jarraitua da puntu guztietan, $x=0$-n izan ezik.

Thomaeren funtzioaren irudikapena (0,1) tartean. Goiko puntuak $f(1/2)=1/2$ irudikatzen du.

Aurreko kasuen antzekoak diren funtzio ez-jarraituetaz gain, funtzio batzuek jokaera patologikoa daukate. Thomaeren funtzioaren kasua da:

$f(x)={\begin{cases}1&x=0{\text{ bada }}\\{\frac {1}{q}}&x={\frac {p}{q}}{\text{(aukerarik txikiena) zenbaki arrazionala bada}}\\0&x{\text{ irrazionala bada}}.\end{cases}}$

Thomaeren funtzioa zenbaki irrazional guztietan jarraitua da, eta ez-jarraitua zenbaki arrazional guztietan. Antzeko era batean, Dirichleten funtzioa ez da inon ez jarraitua

$D(x)={\begin{cases}0&x{\text{ irrazionala bada }}(\in \mathbb {R} \smallsetminus \mathbb {Q} )\\1&x{\text{ arrazionala bada }}(\in \mathbb {Q} )\end{cases}}$

Propietateak

Tarteko balioaren teorema

Tarteko balioaren teorema existentzia teorema bat da, zenbaki errealen osotasunean oinarritua. Honela dio:

$f$ funtzio erreala jarraitua bada $[a,b]$ tarte itxian eta $k$ zenbakia $f(a)$ eta $f(b)$-ren artean badago, orduan exititzen da $c$ zenbaki bat $[a,b]$ tartean non $f(c)=k$.

Adibidez, ume bat 1 m-ko altueratik 1.5 m-ko altuerara hazten bada bi eta sei urte dituen bitartean, orduan, momenturen batean denbora tarte horretan umearen altuera 1.25 m izan da.

Teorema honen ondorioz, $f$ jarraitua bada $[a,b]$ tartean eta $f(a)$ eta $f(b)$-ren zeinuak ezberdinak badira, orduan $[a,b]$ tarteko $c$ puntu batean $f(c)$-ren balioa zero da.

Muturreko balioaren teorema

Muturreko balioaren teoremak (edo Weierstrassen teorema) horrela dio: edozein funtzio $f$ $[a,b]$ tarte batean (edo edozein multzo itxi eta bornatu) definituta badago eta bertan jarraitua bada, orduan funtzioak maximo bat dauka tarte horretan (existitzen da $c\in [a,b]$ non $f(c)\geq f(x)$ $[a,b]$ tarteko $x$ guztientzat). Gauza bera gertatzen da minimoarekin. Orokorrean, emaitza horiek ez dira agertzen funtzioa $(a,b)$ tarte ireki batean definituta dagoenean; $f(x)=1/x$ funtzioaren kasuan adibidez. Funtzio hori definituta dago eta jarraitua da $(0,1)$ tartean, baina ez dauka maximorik ez-bornatua delako goitik.

Jarraitutasunaren erlazioa diferentziagarritasunarekin eta integragarritasunarekin

Edozein funtzio diferentziagarri

$f\colon (a,b)\rightarrow \mathbf {R}$

jarraitua da, frogatu daitekeen bezala. Alderantzizkoa ez da egia: adibidez, balio absolutuaren funtzioa

$f(x)=|x|={\begin{cases}\;\;\ x&{\text{ if }}x\geq 0\\-x&{\text{ if }}x<0\end{cases}}$

edonon jarraitua da. Hala ere, ez da diferentziagarria $x=0$ puntuan (baina beste puntu guztietan bada). Weierstrassen funtzioa puntu guztietan jarraitua da, baina ez da inon ez diferentziagarra.

$f$ funtzio diferentziagarri baten deribatuak $f'(x)$ ez du zertan jarraitua izan. $f'(x)$ jarraitua bada, $f(x)$ jarraituki deribagarria da. Baldintza hori betetzen duten funtzioen multzoa $C^{1}((a,b))$ da. Orokorrean, multzo ireki batetik zenbaki errealetara doazen funtzioen multzoari,

$f\colon \Omega \rightarrow \mathbf {R}$omega

non $f$ $n$ aldiz diferentziagarria den eta $n$-garren deribatua jarraitua den, $C^{n}(\Omega )$ deritzo. Ordenagailu grafikoen arloan, maila horiei $G^{0}$ (posizioaren jarraitutasuna), $G^{1}$ (tangentziaren jarraitutasuna) eta $G^{2}$ (kurbaduraren jarraitutasuna) izenak ematen zaizkie batzuetan.

Edozein funtzio jarraitu

$f\colon [a,b]\rightarrow \mathbf {R}$

integragarria da (Riemannen integralaren zentzuan, adibidez). Alderantzizkoa ez da betetzen, zeinuaren funtzioak (integragarria baina ez-jarraitua) frogatzen duen bezala.

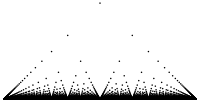
Limite puntual eta uniformeak

Funtzio jarraituen segida bat $f_{n}(x)$ non bere limitea $f(x)$ ez da jarraitua. Konbergentzia ez de uniformea.

Funtzioen segida bat emanda

$f_{1},f_{2},\dotsc \colon I\rightarrow \mathbf {R}$

non limitea

$f(x):=\lim _{n\rightarrow \infty }f_{n}(x)$

definizio eremuko $x$ guztientzat existitzen den, $f(x)$ funtzioa segidaren limite puntuala da. Limite puntual funtzioak ez du zertan jarraitua izan, $f_{n}$ guztiak jarraituak badira ere; eskuinaldeko animazioan ikusten den bezala. Hala ere, $f$ jarraitua da $f_{n}$ funtzio guztiak jarraituak badira eta segida konbergentzia uniformea badauka (konbergentzia uniformearen teoremaren ondorioa). Teorema hori erabili daiteke funtzio esponentzialak, logaritmoak, erro karratu funtzioa eta funtzio trigonometrikoak jarraituak direla frogatzeko.

Jarraitutasun norabidetua eta erdi-jarraitutasuna

• 
  Funtzio eskuin-jarraitu bat
• 
  Funtzio ezker-jarraitu bat

Funtzio ez-jarraituak era mugatuan ez-jarraituak izan daitezkenez, jarraitutasun norabidetuaren (edo eskuin eta ezker-jarraitutasuna) eta erdi-jarraitutasunaren kontzeptuak agertzen dira. Intuitiboki, funtzio bat eskuin-jarraitua da ez badago jauzirik limitearen puntura hurbiltzean eskuinetik. Formalki, $f$ eskuin-jarraitua da $c$ puntuan hurrengoa betetzen baldin bada: edozein $\varepsilon >0$-rentzat existitzen da $\delta >0$ non $c<x<c+\delta$ betetzen duten $x$ guztientzat

$|f(x)-f(c)|<\varepsilon .$

Baldintza hau eta funtzio jarraituena ia berdinak dira: kasu honetan $c$ baino handiagoak diren $x$-tarako bakarrik bete behar da. Aldiz, eskatzen bada baldintza betetzea $c-\delta <x<c$ betetzen duten $x$-tarako, ezker-jarraitutasuna agertzen da. Funtzio bat jarraitua da baldin eta soilik baldin ezker eta eskuin-jarraitua bada.

Funtzio bat behe erdi-jarraitua da baldin egon daitezkeen jauziak behera badoaz, eta ez gora. Hau da, edozein $\varepsilon >0$-rentzat existitzen da $\delta >0$ non $|x-c|<\delta$ betetzen duen eta definizio-eremuan dagoen edozein $x$-rentzat hurrengoa betetzen den:

$f(x)\geq f(c)-\varepsilon .$

Alderantzizko baldintza goi erdi-jarraitua da.

Espazio metrikoen arteko funtzioen jarraitutasuna

Funtzio erreal jarraituen kontzeptua espazio metrikoen arteko funtzioetara orokortu daiteke. Espazio metriko bat $X$ multzo bat da, funtzio batez ($d_{X}$) hornituta dagoena (metrika deritzo). Funtzio honen ideia intuitiboa $X$-ko bi elementuen arteko distantzia da. Formalki, metrika honako funtzioa da:

$d_{X}\colon X\times X\rightarrow \mathbf {R}$

Funtzio honek zenbait propietate betetzen ditu, desberdintza triangeluarra nabarmenki. Bi espazio metriko ($(X,d_{X})$ eta $(Y,d_{Y})$ ) eta funtzio bat emanda,

$f\colon X\rightarrow Y$

orduan $f$ jarraitua da $c$ puntuan ($X$-n) emandako metrikarekiko, baldin eta edozein $\varepsilon$ positiborako existitzen bada $\delta$ positiboa non $d_{X}(x,c)<\delta$ betetzen duten $X$-ko edozein $x$-k $d_{X}(f(x),f(c))<\varepsilon$ betetzen badu. Gainera, aurreko kasuko funtzio errealetan bezala; $c$ limitea duen $X$-ko edozein $\{x_{n}\}$ segidarentzentat $\lim f(x_{n})=f(c)$ betetzea jarraitutasunaren definizo baliokidea da. Azken baldintza hau honako eran ahuldu daiteke: $f$ jarraitua da $c$-n baldin eta solik baldin $c$ limitea duen $X$-ko edozein segida $\{x_{n}\}$ konbergenterentzat $f(x_{n})$ Caucyren segida bada eta $c$ $f$-ren domeinuan badago.

Espazio metrikoen arteko funtzio bat jarraitua den puntuetaz osatutako multzoa G_δ da, ε-δ jarraitutasunaren definizoaren ondorioa dena.

Jarraitutasunaren ideia hau erabiltzen da, adibidez, analisi funtzionalean. Adar onetako oinarrizko proposizio batek dio $V$ eta $W$ bektore espazio normaduen arteko operadore lineal bat

$T\colon V\rightarrow W$

jarraitua dela baldin eta solik baldin bornatua bada, hau da, existitzen da $K$ konstante bat non

$\|T(x)\|\leq K\|x\|$

$x\in V$ edozeinerako.

Jarraitutasun uniformea, Hölderriarra eta Lipschitziarra

Funtzio Lipschitziar batentzat, kono bikoitza existizen da (zuriz). Bere bertizea mugitu daiteke grafoan zehar, grafoa beti konoaren kanpoan dagoelarik.

Espazio metrikoen arteko funtzioen jarraitutasuna zenbait eratan sendotu daiteke, mugatuz $\delta$-ren menpekotasuna $\varepsilon$ eta $c$-rekiko (aurreko definizioan). Intuitiboki, $f$ funtzioa uniformeki jarraitua da $\delta$ ez bada $c$ puntuaren menpekoa. Zehazki, beharrezkoa da edozein $\varepsilon$ positiborentzat existitzea $\delta$ positiboa non $d_{X}(b,c)<\delta$ betetzen duten edozein $b,c\in X$-rentzat $d_{Y}(f(b),f(c))<\varepsilon$ izatea. Beraz, edozien funtzio uniformeki jarraitu jarraitua da. Alderantzizkoa ez da betetzen orokorrean, baina betetzen da $X$ trinkoa bada. Aplikazio uniformeki jarraituak espazio uniformeen egoera orokorreagoan definitu daitezke.

Funtzio bat Hölderriarra da $\alpha$ berretzailearekin (zenbaki erreala), existitzen bada $K$ konstantea non $X$-ko edozein $b$ eta $c$-rentzat hurrengo desberdintza betetzen den:

$d_{Y}(f(b),f(c))\leq K\cdot (d_{X}(b,c))^{\alpha }$

Edozein funtzio Hölderriar uniformeki jarraitua da. $\alpha =1$ kasu bereziari Lipschitzen jarraitutasuna deritzo. Hau da, funtzio bat Lipschitziarra da hurrengo desberdintza betetzen duen $K$ konstantea existitzen bada

$d_{Y}(f(b),f(c))\leq K\cdot d_{X}(b,c)$

$X$-ko edozein $b$ eta $c$-rentzat. Lipschitzen baldintza agertzen da adibidez, Picard–Lindelöf teoreman, ekuazio diferentzial arrunten soluzioetaz arduratzen dena.

Espazio topologikoen arteko funtzioen jarraitutasuna

Jarraitutasunaren beste kontzeptu abstraktuagoa espazio topologikoen arteko funtzioen jarraitutasuna da, non orokorrean ez dago distantziarik, espazio metrikoen kasuan bezala. Espazio topologiko bat $X$ multzo bat da beraren gaineko topologia batekin. $X$-ren gaineko topologia $X$-ren azpimultzoen multzoa da. Azpimultzoen arteko bildurei eta ebakidurei buruzko zenbait propietate bete behar dira: propietate horiek espazio metrikoetako bola irekien propietateak orokortzen dituzte, puntu baten ingurunea oraindik definituta dagoen bitartean. Topologia baten elementuei $X$-ren azpiultzo ireki deritze ($X$-ren topologiarekiko).

$X$ eta $Y$ espazio topologikoen arteko funtzioa

$f\colon X\rightarrow Y$

jarraitua da baldin eta $VcY$ edozein multzo irekirentzat bere aurreirudia

$f^{-1}(V)=\{x\in X\;|\;f(x)\in V\}$

$X$-ren azpimultzo irekia den. Hau da, $f$ $X$ eta $Y$-ren arteko funtzioa da, baina $f$-ren jarraitutasuna $X$ eta $Y$-ren gaineko topologien menpekoa da.

Baldintza horren baliokidea da $Y$-ko multzo itxien (multzo irekien osagarriak) aurreirudiak $X$-n itxiak izatea.

Adibidez, $X$ multzoari topologia diskretua (azpimultzo guztiak irekiak) ematen bazaio, $T$ espazio topologikorainoko funtzio guztiak

$f\colon X\rightarrow T$

jarraituak dira. Aldiz, $X$-ri topologia indiskretua (azpimultzo ireki bakarrak multzo hutsa eta $X$ dira) ematen bazaio, eta $T$ espazioa gutxienez T₀ bada, orduan funtzio jarraitu bakarrak funtzio konstanteak dira. Alderantziz, irudi indiskretua duen edozein funtzio jarraitua da.

Puntu bateko jarraitutasuna

Puntu bateko jarraitutasuna: f(x)-ren edozein V ingurunerentzat, existizen da x-ren ingurunea U non f(U) ⊆ V.

Epsilon-delta erako jarraitutasunaren definizioaren itzulpena inguruneen hizkuntzara puntu bateko jarraitutasunaren definiziora eramaten du:

«

$f:X\rightarrow Y$ funtzioa jarraitua da $x\in X$ puntuan baldin eta soilik baldin $f(x)$-ren edozein ingurune $V$-rentzat $x$-ren ingurune bat $U$ existizen bada non $f(U)\subseteq V$.

»

Definizio honen baliokidea da definizio bera baina ingurune irekietara murriztuta. Gainera, hainbat eratan berridatzi daiteke, irudien ordez aurreirudiak erabiliz.

Gainera, ingurune bat daukan edozein multzo ingurune bat denez, eta $f^{-1}(V)$ $U$-ren azpimultzorik handiena denez non $f(U)\subseteq V$; definizio hau horrela sinplifikatu daiteke:

«

$f:X\rightarrow Y$ funtzioa jarraitua da $x\in X$ puntuan baldin eta soilik baldin $f^{-1}(V)$ $x$-ren ingurunea bada $f(x)$-ren edozein $V$ ingurunerentzat.

»

Multzo ireki bat bere puntu guztien ingurunea den multzoa denez, $f:X\rightarrow Y$ funtzioa jarraitua da $X$-ren edozein puntutan baldin eta soilik baldin funtzio jarraitua bada.

$X$ eta $Y$ espazio metrikoak badira, baliokidea da $x$-n zentratutako bola irekien ingurune sistema kontuan hartzea, ingurune guztiak baino. Honek epsilon-delta jarraitutasunaren definizioa bueltatzen du espazio metrikoetan. Espazio topologiko orokorretan, ez dago ez distantziarik ez hurbiltasunik. Hala ere, jomuga espazioa Hausdorff bada, oraindik ere egia da $f$ jarraitua dela $a$-n baldin eta soilik baldin $f$-ren limitea $a$-ra hurbiltzen den heinean $f(a)$ bada. Puntu isolatu batean, edozein funtzio jarraitua da.

Ordezko definizioak

Egitura topologikoen hainbat definizio baliokide daude, eta beraz zenbait definizio baliokide existitzen dira funtzio jarraitu bat definitzeko.

Segidak eta sareak

Hainbat testuingurutan, espazioaren topologia metaketa puntuen bidez definitzen da. Zenbait kasuetan, hori lortzen da argituz noiz puntu bat segida baten limitea den, baina espazio handiago batzuetan, zehaztu behar da noiz puntu bat sare baten limitea den. Funtzio bat jarraitua (Heinearra) da baldin eta segiden limiteak segiden limitetara eramaten baditu. Lehengo kasuan, limiteen kontserbazioa baldintza nahikoa da; bigarrenean funtzio batek segiden limiteak kontserbatu ditzake eta jarraitua ez izan, baina sareen kontserbazioa baldintza beharrezkoa eta nahikoa da.

Zehazki, $f:X\rightarrow Y$ funtzioa segidaki jarraitua da baldin $f(x_{n})$ segidak $x$ limitea badu, $x_{n}$ $x$ limitea duen $X$-ko $x_{n}$ segida izanda. Hortaz, segidaki jarraituak diren funtzioak segiden limiteak kontserbatzen dituzte. Funtzio jarraitu guztiak segidaki jarraituak dira. $X$ espazio lehen-kontagarria bada eta aukera kontagarria betetzen bada, orduan alderantzizkoa ere betetzen da: segiden limiteak kontserbatzen dituen funtzioa bat jarraitua da. Hain zuzen, $X$ espazio metrikoa bada jarraitutasuna eta segidako jarraitutasuna baliokideak dira. Lehen-kontagarriak ez diren espazioetan, segidako jarraitutasuna jarraitutasuna baino ahulagoa izan daiteke. Arrazoi honengatik, espazio topologikoen testuinguruan, sareak erabiltzen dira segidak baino. Funtzio jarraituek sareen limiteak kontserbatzen dituzte, izan ere propietate hori jarraitutasunaren karakterizazioa da.

Itxidura eragileen bitarteko definizioa

Espazio topologiko baten azpimultzo irekiak zehaztu beharrean, topologia itxidura eragileen ($cl$ izendatuta) bitartez definitu daiteke; $cl$-k $A\subseteq X$ edozein azpimultzo bere itxidurara bidaltzen du. $int$ barrualde eragileak $A\subseteq X$ edozein azpimultzori bere barrualdea esleitzen dio. Beraz, espazio topologikoen arteko funtzio bat

$f\colon (X,\mathrm {cl} )\to (X',\mathrm {cl} ')$

jarraitua da aurreko zentzuan baldin eta soilik baldin $A\subseteq X$ azpimultzo guztientzat

$f(\mathrm {cl} (A))\subseteq \mathrm {cl} '(f(A)).$

Hau da, $A$-n dagoen $X$-ko edoezein $x$ hartuta, $f(x)$ $f(A)$-ren itxiduran dago. Horren baliokidea da esatea $A\subseteq X$ azpimultzo guztientzat hurrengoa betetzen dela:

$f^{-1}(\mathrm {cl} '(A'))\supseteq \mathrm {cl} (f^{-1}(A')).$

Gainera,

$f\colon (X,\mathrm {int} )\to (X',\mathrm {int} ')$

jarraitua da baldin eta soilik baldin

$f^{-1}(\mathrm {int} '(A'))\subseteq \mathrm {int} (f^{-1}(A'))$

betetzen bada $A'\subseteq Y$ edozeinentzat.

Propietateak

$f:X\rightarrow Y$ eta $g:Y\rightarrow Z$ jarraituak badira, $g\circ f:X\rightarrow Z$ ere jarraitua da. $f:X\rightarrow Y$ bada eta

• $X$ trinkoa bada, orduan $f(X)$ trinkoa da.
• $X$ konexua bada, orduan $f(X)$ konexua da.
• $X$ Lindelöf bada, orduan $f(X)$ Lindelöf da.
• $X$ banangarria bada, orduan $f(X)$ banangarria da.

$X$ finkatutako multzo baten gaineko topologia posibleak partzialki ordenatuta daude: $\tau _{1}$ topologia lodiagoa da $\tau _{2}$ topologia baino ($\tau _{1}\subseteq \tau _{2}$) $\tau _{1}$-eko edozein azpimultzo ireki $\tau _{2}$-n irekia bada. Ondorioz, $id_{X}$ identitatea

$id_{X}:(X,\tau _{2})\rightarrow (X,\tau _{1})$

jarraitua da baldin eta soilik baldin $\tau _{1}\subseteq \tau _{2}$ bada. Orokorrean, funtzio jarraitu bat

$(X,\tau _{X})\rightarrow (Y,\tau _{Y})$

jarraitua izaten jarraitzen du $\tau _{Y}$ topologia beste topologia lodiago batengatik trukatzen bada, edo $\tau _{X}$ topologia beste topologia finago batengatik trukatzen bada.

Homeomorfismoak

Aplikazio jarraituaren kontzeptuaren antzekoa da aplikazio irekiarena, non multzo irekien irudiak irekiak dira. Egitan, $f$ aplikazio irekiak alderantzizkoa badauka, alderantzizkoa irekia da; eta $g$ aplikazio jarraituak alderantzizkoa badu, alderantzizkoa irekia da. Bi espazio topologikoen arteko $f$ bijekzio bat emanda, $f^{-1}$ alderantzizkoak ez du zertan jarraitua izan. Aplikazio bijektibo bat alderantzizko jarraituarekin homeomorfismoa da.

Bijekzio jarraitu baten definizio-eremua trinkoa bada eta bere koeremua Hausdorff bada, orduan homeomorfismoa da.

Topologien definizioa funtzio jarraituen bitartez

Funtzio bat emanda

$f\colon X\rightarrow S,$

non $X$ espazio topologika den eta $S$ multzo bat (topologiarik gabe), $S$-ren gaineko topologia finala definitu daiteke. $S$-ren multzo irekiak izango dira $S$-ren $A$ azpimultzoak non $f^{-1}(A)$ irekia den $X$-n. $S$-k aurretik topologia bat badauka, $f$ topologia horrekiko jarraitua da baldin eta soilik baldin aurretiko topologia topologia finala baino lodiagoa bada. Hortaz, $S$-ren topologiarik finena non $f$ jarraitua den topologia finalaren karakterizazio bat izango da. $f$ supraiektiboa bada, topologia hori kanonikoki identifika daiteke koziente topologiarekin, $f$-k definitutako baliokidetasun-erlazioaren bitartez.

Gainera, $S$ multzotik $X$ espazio topologiko batera doan $f$ funtzio batentzat; $S$-ko hasierako topologiaren irekiak $S$-ren $A$ azpimultzoak izango dira non $A=f^{-1}(U)$, $X$-ko $U$ ireki batentzat. $S$-k aurretik topologia bat badauka, $f$ topologia horrekiko jarraitua da baldin eta soilik baldin aurretiko topologia hasierako topologia baino finagoa bada. Hortaz, $S$-ren topologiarik lodiena non $f$ jarraitua den hasierako topologiaren karakterizazio bat izango da. $f$ injektiboa bada, topologia hori kanonikoki identifika daiteke $S$-ren azpiespazio topologiarekin, $X$-ren azpimultzotzat hartuz.

$S$ multzo baten gaineko topologia bat determina daiteke $S\rightarrow X$ funtzio jarraitu guztien klaseen bitartez, $X$ edozein espazio topologiko izanda. Dualki, antzeko ideia erabili daiteke $X\rightarrow S$ funtzioekin.

Lotutako kontzeptuak

Matematikako beste adar batzuek jarraitutasun kontzeptua erabiltzen dute esanahi ezberdin baina erlazionatuekin. Adibidez, ordena teorian, ordena mantentzen duen $f\colon X\rightarrow Y$ funtzioa $X$ eta $Y$ partzialki ordenatutako multzoen artean jarraitua da baldin eta $X$-ren azpimultzo bideratu bakoitzarentzat $\sup(f(A))=f(\sup(A))$ betetzen bada. Hemen, $\sup$ $X$ eta $Y$-ren ordenaketekiko gorena da. Jarraitutasun kontzeptu hau jarraitutasun topologikoaren berdina da partzialki ordenatutako multzoek Scotten topologia daukatenean.

Kategoria teorian, bi kategorien arteko funktorea

$F\colon {\mathcal {C}}\rightarrow {\mathcal {D}}$

jarraitua da baldin eta limite txikiekin konmutatzen badu. Hau da:

$\varprojlim _{i\in I}F(C_{i})\cong F\left(\varprojlim _{i\in I}C_{i}\right)$

edozein objektu-diagrama txikiarentzat ${\mathcal {C}}$-n.

Jarraitutasun espazioa espazio metriko eta poseten orokortzea da, quantalen kontzeptua erabiltzen duena eta espazio metrikoen eta domeinuen nozioa bateratzeko erabili daitekena.

Bestelakoak

Jarraitutasun simetrikoa

Funtzio bat $f:\mathbb {R} \to \mathbb {R}$ simetrikoki jarraitua da $x$ puntuan hurrengoa betetzen bada:

$\lim _{h\to 0}f(x+h)-f(x-h)=0.$

Jarraitutasunaren definiziorik arruntenak jarraitutasun simetrikoa inplikatzen du, baina alderantzizkoa ez da egia. Adibidez, $x^{-2}$ funtzioa simetrikoki jarraitua da $x=0$ puntuan, baina ez da jarraitua.

Gainera, diferentziagarritasun simetrikoak jarraitutasun simetrikoa inplikatzen du, baina alderantzizkoa ez da egia (jarraitutasun normalaren kasuan bezala, diferentziagarritasunik ez du inplikatzen).

See also

• Absolute continuity
• Classification of discontinuities
• Coarse function
• Continuous stochastic process
• Dini continuity
• Equicontinuity
• Normal function
• Piecewise
• Symmetrically continuous function

References

• Txantiloi:Springer